328. Найти общее решение
дифференциального уравнения x2y’–2xy=3.
Решение.
x2y’–2xy=3
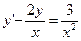
Найдем решение однородного
уравнения.
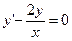
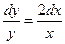
lny=2lnx+lnC
y=cx2
Решение исходного уравнения
найдем методом вариации постоянной.
c=c(x)
y’=c’x2+2cx
x2y’–2xy=3
c’x4+2cx3–2cx3=3
c’x4=3
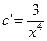
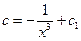
В результате получаем общее
решение исходного уравнения.
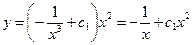
348. Найти частное решение
дифференциального уравнения y”–4y’=6x2+1, удовлетворяющее
начальным условиям y(0)=2;
y’(0)=3.
Решение.
Найдем решение
характеристического уравнения.
k2–4k=0
k=0;4
Получаем общее решение
однородного уравнения.
yoo = C1e4x+C2
Найдем частное решение
неоднородного уравнения.
Поскольку в правой части
уравнения стоит многочлен, то частное решение неоднородного уравнения будем
искать в виде многочлена.
yчн=Ax3+Bx2+Cx
y’=3Ax2+2Bx+C
y”=6Ax+2B
y”–4y’=6x2+1
6Ax+2B–12Ax2–8Bx–4C=6x2+1
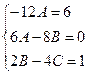
A=–0.5
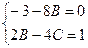
B=–0.375
–0.75–4C=1
4C=–1.75
C=–0.4375
yчн=–0.5x3–0.375x2–0.4375x
Получаем общее решение
y= C1e4x+C2–0.5x3–0.375x2–0.4375x
y’=4C1e4x–1.5x2–0.75x–0.4375
C1+C2=2
4C1=3
C1=0.75
C2=1.25
Получаем частное решение.
y= 0.75e4x+1.25–0.5x3–0.375x2–0.4375x
368. Кривая проходит через точку А(1;2)
и обладает тем свойством, что отношение ординаты любой ее точки к абсциссе
пропорционально угловому коэффициенту касательной к этой кривой, проведенной в
той же точке, с коэффициентом пропорциональности k=3. Найти уравнение кривой.
Решение.
Угловой коэффициент касательной к
кривой в какой-либо точке равен производной функции в этой точке. Исходя из
этого, получим дифференциальное уравнение.
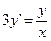
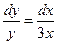
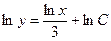
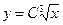
Постоянную С можно найти из
соотношения y(1)=2
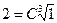
C=2
Получаем уравнение искомой кривой
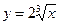
428. Исследовать сходимость
числового ряда 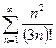 .
.
Решение.
Воспользуемся признаком Даламбера
сходимости ряда.
Найдем 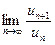 =
= 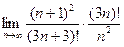 =
= 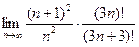 =
= 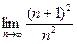 ·
· 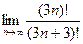 =
= 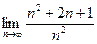 ·
· 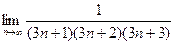 =
= 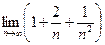 ·
· 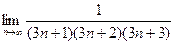 = 1·0 = 0
= 1·0 = 0
Следовательно, ряд сходится.
438. Найти интервал сходимости
степенного ряда 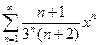 .
.
Решение.
Воспользуемся признаком Даламбера
сходимости ряда.
Найдем 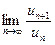 =
= 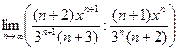 =
= 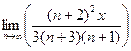 =
= 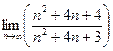 ·
· 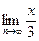 =
= 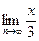
Получаем интервал сходимости (–3;3).