102. Уравнения движения двух материальных точек по прямой: x₁ = A₁+B₁t+C₁t², где A₁=20 м, B₁=12м/с, C₁=–4м/с², и x₂ = A₂+B₂t+C₂t², где A₂=2 м, B₁=2м/с, C₁=0.5м/с². В какой момент времени скорости этих точек будут одинаковыми? Чему равны скорости и ускорения точек в этот момент?

Решение.

Найдем уравнение изменения скорости этих материальных точек с течением времени.

v₁=(x₁)’_t = 12–8t

v₂=(x₂)’_t = 2+t

Найдем момент времени, в который скорости точек равны друг другу.

12–8t=2+t

9t=10

t=10/9 с.

Скорость точек в этот момент времени будет равна 2+10/9 = 28/9 м/с.

Найдем уравнение изменения ускорения этих материальных точек с течением времени.

a₁=(v₁)’_t =–8

a₂=(v₂)’_t =1

Мы получили, что ускорения данных точек не зависят от времени. Ускорение первой точки будет равно (–8) м/с², а ускорение второй – 1 м/с².

112. На горизонтальной поверхности лежит тело массой m=5 кг. Какой путь пройдет это тело за t=1 с, если к нему приложить силу F₁=50 Н, образующую угол α=60° с горизонтом? Коэффициент трения между телом и поверхностью принять равным n=0.2.

Решение.

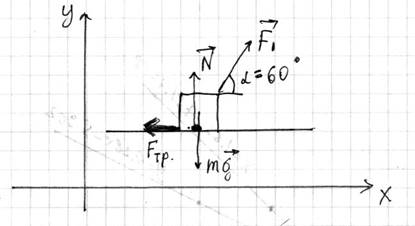
Запишем уравнение движения тела согласно второму закону Ньютона.

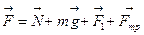, где F – равнодействующая всех действующих на тело сил

В проекции на оси координат.

0=N+F₁sinα–mg

F=F₁cosα–F_тр

Подставив известные значения, получим:

0=N+50∙sin60°–5∙10 (на ось y)

F=50∙cos60°–F_тр (на ось x)

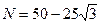
Учитывая, что F_тр = nN, получим:

 =  =

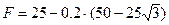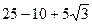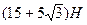
Мы получили величину равнодействующей сил, действующих на тело.

Найдем ускорение тела.

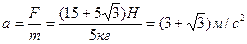
Путь, который пройдет тело, начавшее двигаться с нулевой начальной скоростью и ускорением a равен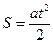

Подставив значения 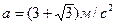 и t=1с, получим:

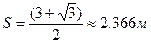
122. Снаряд, летевший со скоростью 400 м/с, разорвался на 2 осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью 150 м/с. Определить скорость большого осколка (по величине и по направлению).

Решение.

Обозначим массу снаряда за единицу, v – скорость второго осколка после разрыва.

Согласно закона сохранения импульса получим:

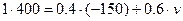
400=–60+0.6v

0.6v=460

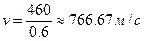
132. Найти работу, совершаемую при подъеме груза массой 10 кг по наклонной плоскости с углом наклона 45⁰ на расстояние 2 м, если время подъема – 2 с, а коэффициент трения μ=0.1.

Решение.

Согласно условиям задачи покоящееся тело, двигаясь равноускоренно, за две секунды проходит расстояние в 2 м. Уравнение равноускоренного движения тела без начальной скорости 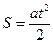. Выразив ускорение, получим 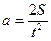. Подставив значения, получим: a=1 м/с². Сила, действующая на тело, равна F=ma=10 кг·м/с²=10 Н. Совершаемая работа равна А= Fs=10 Н·2 м=20 Дж.

142. На барабан радиусом 20 см, момент инерции которого равен 0.1 кг·м², намотан шнур, к которому привязан груз массой 0.5 кг. До начала вращения барабана высота груза над полом равна 1 м. Найти: 1) через сколько времени груз опустится до пола; 2) кинетическую энергию груза в момент удара о пол. Трением пренебречь.

Решение.

Из формулы момента инерции 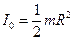 выразим массу барабана. Получим формулу 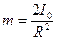. Подставив значения, получим 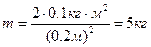. Барабан начинает вращаться в результате действия силы, равной 0.5 кг·10 м/с²=5 Н. Эта сила сообщит ободу барабана линейное ускорение равное 5Н:5кг=1м/с².

1) Так как первоначальная высота груза над полом равна 1м, то время, за которое груз опустится до пола, можно найти из соотношения 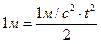. Выразив t, получим .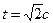

2) Скорость груза в момент удара о пол будет равна 1 м/с²·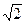с=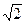м/с. Кинетическая энергия груза в этот момент будет равна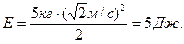

152. Определить высоту наклонной плоскости, если линейная скорость центра шара, скатившегося без скольжения с наклонной плоскости равна 2.65 м/с. Начальная скорость шара равна нулю.

 

Решение.

При скатывании тела с наклонной плоскости высотой h его потенциальная энергия переходит в кинетическую поступательного и вращательного движения. По закону сохранения энергии:

,

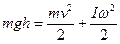где I – момент инерции тела, m – масса.

Момент инерции шара равен: 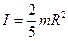. Учитывая это, получим:

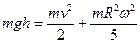
Согласно формуле связи между линейной и угловой скоростями, имеем v=ωR. Таким образом, получаем:

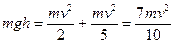
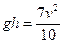
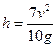
Подставив значения, получим

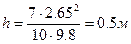
202. Два точечных заряда q₁=2∙10^-7 Кл и q₂=4∙10^-7 Кл находятся на расстоянии 6,5 см друг от друга. Найти положение точки, в которой напряженность статического поля E равна нулю. Рассмотреть случай одноименных зарядов.

Решение.

Так как заряды одноименные, то искомая точка будет находится на отрезке, соединяющем данные заряды. Обозначим расстояние от искомой точки до первого заряда s₁.

Обозначим E₁ – напряженность поля первого заряда в искомой точке, E₂ – напряженность поля второго заряда в искомой точке.

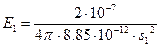
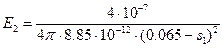
По условию задачи E₁=E₂

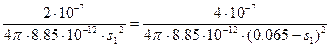
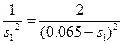
(0.065–s₁)²=2s₁²

0.004225–0.13s₁+s₁²=2s₁²

s₁²+0.13s₁–0.004225=0

D=0.0169+0.0169=0.0338

 =  =  =

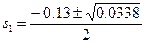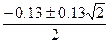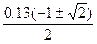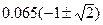
Т.к. 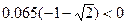, то единственным подходящим решением будет: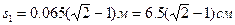

212. Расстояние между пластинами плоского конденсатора d=2 мм, разность потенциалов равна 600 В. Заряд каждой пластины q=40 нКл. Определить энергию поля конденсатора и силу взаимного притяжения пластин.

Решение.

Электроемкость конденсатора

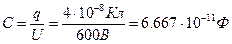
Энергия поля конденсатора

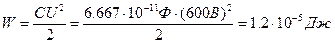
Сила взаимного притяжения пластин.

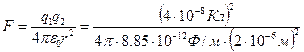 = 3.5776·10⁶ Н

222. Аккумулятор с внутренним сопротивлением 1 Ом подключен для зарядки к сети напряжением 12.5 В. Найти ЭДС аккумулятора, если при зарядке через него проходит ток 0.5 А.

Решение.

Воспользуемся законом Ома для участка цепи, содержащего ЭДС.

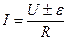
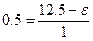
ε=12 В.

232. По контуру в виде равностороннего треугольника проходит ток I = 40 А. Сторона треугольника a=30 см. Найти магнитную индукцию B поля в точке пересечения высот.

Решение.

Магнитная индукция поля, созданного отрезком проводника с током:

.

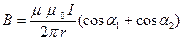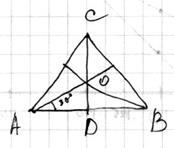
Из рисунка видно, что α₁= α₂=30º.

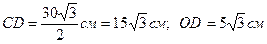
Найдем значение магнитной индукции от одного проводника.

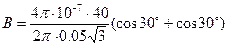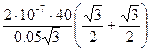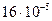 =  =  = 0.00016Тл

Т.к. проводника три, то итоговая индукция равна

3∙0.00016Тл=0.00048Тл

242. Электрон влетает в однородное магнитное поле перпендикулярно силовым линиям. Скорость электрона v=2·10⁷ м/с, индукция магнитного поля равна 4·10^-3 Тл. Чему равно тангециальное и нормальное ускорение электрона в магнитном поле.

Решение.

Тангенциальное ускорение электрона будет равно 0.

Найдем нормальное (центростремительное) ускорение электрона.

Сила Лоренца, действующая на электрон равна F = qvB = 1.6·10^–19 Кл· 2·10⁷ м/с· 4·10^–3 Тл = 1.28·10^–14Н

Соответственно, нормальное ускорение электрона будет равно a = F/m = 1.28·10^–14Н / 9.1·10^–31 кг = 1.4·10¹⁸м/с²

252. Виток, в котором поддерживается постоянная сила тока 2 А, расположен в плоскости магнитного меридиана. Диаметр витка равен 50 см. Какую работу надо совершить, чтобы повернуть виток на угол 80⁰ относительно оси, перпендикулярной и совпадающей с диаметром. Напряженность магнитного поля Земли принять равной 16.3 А/м.

Решение.

Магнитная индукция

B = μ₀H = 4π·10^–7Гн/м·16.3А/м = 2.05·10^–5 Тл

Площадь кольца равна

S=πr² = 3.14159265·(0.5м)² = 0.7854м²

Изначально угол α между вектором магнитной индукции и нормалью к площадке равен 90º. После поворота этот угол составит 10º

Найдем значение потока вектора магнитной индукции в первом и во втором случаях.

В первом случае

Ф=BScos90º = 0

Во втором случае

Ф=BScos10º = 2.05·10^–5 Тл · 0.7854 м² · 0.9848 = 1.5856·10^–5 Вб

Искомая работа равна

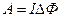 = 2А·1.5856·10^–5 Вб = 3.1712·10^–5Дж.