Контрольная работа № 1.
В задачах 1–20 даны координаты вершин треугольника ABC. Сделать чертеж и найти:
1) длины и уравнения сторон треугольника; 2) уравнение высоты AD; 3) уравнение медианы СМ; 4)
уравнение вписанной окружности.
12. A(3;1),
B(–13;–11), C(–6;13)
Решение.
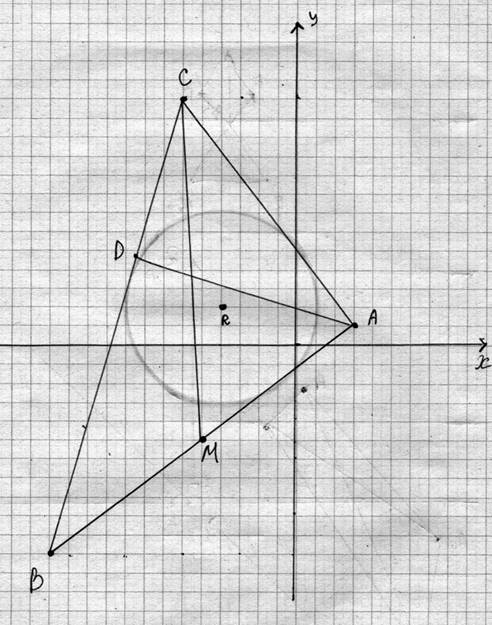
1) Длина стороны AB.
|AB|
= 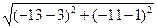 =
= 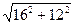 =
= 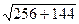 =
= 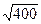 = 20
= 20
Уравнение стороны AB.
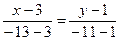
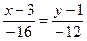
–12x+36=–16y+16
12x–16y–20=0
3x–4y–5=0
Длина стороны BC.
|BC| = 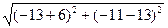 =
= 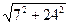 =
= 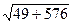 =
= 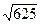 = 25
= 25
Уравнение стороны BC.
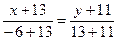
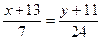
24x+312=7y+77
24x–7y+235=0
Длина стороны AC.
|AC| = 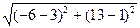 =
= 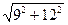 =
= 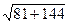 =
= 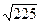 = 15.
= 15.
Уравнение стороны AC.
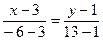
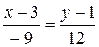
12x–36=–9y+9
12x–9y–45=0
4x–3y–15=0
2) Уравнение высоты AD.
Общее уравнение перпендикуляра к стороне BC.
7x+24y+C1=0
Искомая прямая проходит через точку A.
7∙3+24∙1+C1=0
21+24+C1=0
C1=–45.
Уравнение высоты AD.
7x+24y–45=0
3) Уравнение медианы CM.
Середина стороны AB – точка M.
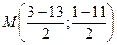
M(–5;–5)
Уравнение медианы CM.
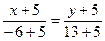
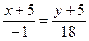
18x+90=–y–5
18x+y+95=0
4) уравнение вписанной окружности.
Центром вписанной окружности треугольника является точка
пересечения биссектрис.
Найдем уравнение биссектрисы угла A.
Для нахождения уравнения биссектрисы AN достаточно найти направляющий вектор
этой прямой в качестве которого можно взять s=AB0+AC0, где AB0 – орт вектора AB, равный 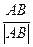 , AC0
– орт вектора AC.
, AC0
– орт вектора AC.
Найдем орты.
AB0
= 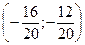
AС0
= 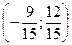
AN =
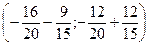 =
= 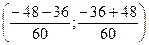 =
= 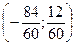 =
= 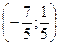
Так как длина направляющего вектора значения не имеет, то
этот вектор можно умножить на любую константу.
(–7;1)
Уравнение биссектрисы AM.
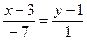
x–3=–7y+7
x+7y–10=0
Найдем уравнение биссектрисы BP.
Найдем орты.
BC0
= 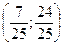
BA0
= 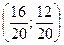
BP =
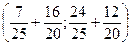 =
= 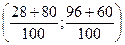 =
= 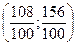 =
= 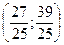
Так как длина направляющего вектора значения не имеет, то
этот вектор можно умножить на любую константу.
(27;39)
(9;13);
Уравнение биссектрисы BP.
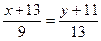
13x+169=9y+99
13x–9y+70=0
Точка пересечения биссектрис.
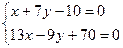
x=–7y+10
–91y+130–9y+70=0
–100y+200=0
y=2
x+14–10=0
x=–4
Точка пересечения биссектрис R(–4;2), будет центром
вписанной окружности треугольника.
Найдем радиус вписанной окружности треугольника.
Согласно известной формуле
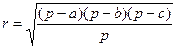 , где p – полупериметр треугольника.
, где p – полупериметр треугольника.
p=(15+20+25)/2=30.
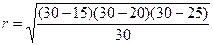 =
= 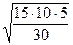 = 5.
= 5.
Получили уравнение вписанной окружности.
(x+4)2+(y–2)2=25
В задачах 21–40 даны координаты вершин пирамиды A1A2A3A4. Найти 1) длину
ребра A1A2; 2) угол между
ребрами A1A2 и A1A4; 3) угол между
ребром А1A4
и гранью A1A2A3; 4) площадь
грани A1A2A3; 5) объем
пирамиды; 6) уравнение прямой A1A2; 7) уравнение
плоскости A1A2A3; 8) уравнение
высоты, опущенной из вершины A4
на грань A1A2A3. Сделать
чертеж.
32. A1(–4;2;8),
A2(–4;8;0), A3(–2;6;2), A4(–9;4;2).
Решение.
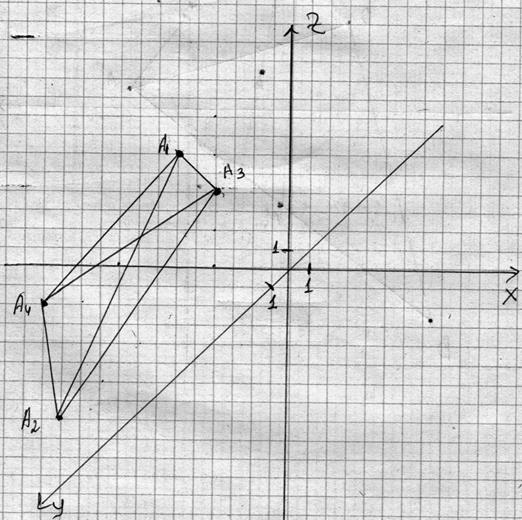
1) Длина ребра A1A2.
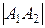 =
= 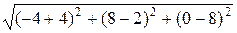 =
= 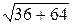 = 10.
= 10.
2) угол между ребрами A1A2
и A1A4.
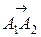 = (–4+4;8–2;0–8) = (0;6;–8)
= (–4+4;8–2;0–8) = (0;6;–8)
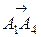 = (–9+4;4–2;2–8) = (–5;2;–6)
= (–9+4;4–2;2–8) = (–5;2;–6)
cos φ
= 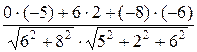 =
= 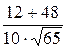 =
= 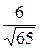 = 0.7442
= 0.7442
φ
= arccos 0.7442 =
0.73146 = 41.9°
3) угол между ребром А1A4 и гранью A1A2A3.
Уравнение прямой А1A4.
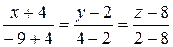
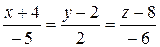
Уравнение плоскости A1A2A3.
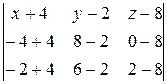 =
= 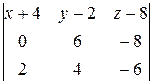 =
(–4)(x+4)–16(y–2)+(–12)(z–8) = –4x–16–16y+32–12z+96 = –4x–16y–12z+112
=
(–4)(x+4)–16(y–2)+(–12)(z–8) = –4x–16–16y+32–12z+96 = –4x–16y–12z+112
Получаем уравнение плоскости
–4x–16y–12z+112=0
x+4y+3z–28=0
Угол между прямой и плоскостью
sin φ
= 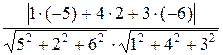 =
= 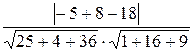 =
= 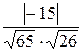 =
= 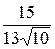 = 0.365
= 0.365
φ
= arcsin 0.365 = 0.3736
= 21.4°
4) площадь грани A1A2A3.
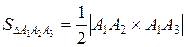
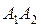 = (0;6;–8)
= (0;6;–8)
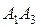 = (–2+4;6–2;2–8) = (2;4;–6)
= (–2+4;6–2;2–8) = (2;4;–6)
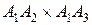 =
= 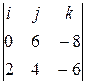 =
= 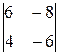 i –
i – 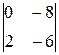 j +
j + 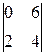 k = –4i – 16j
– 12k
k = –4i – 16j
– 12k
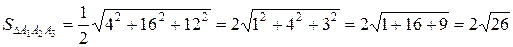
5) Объем пирамиды равен 1/6 объема параллелепипеда,
построенного на векторах A1A2, A1A3 и A1A4;
V = 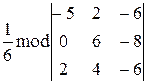 =
= 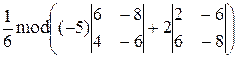 =
= 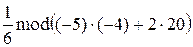 =
= 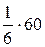 = 10.
= 10.
6) уравнение прямой A1A2.
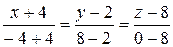
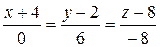
Равенство нулю знаменателя первой дроби означает, что прямая
лежит в плоскости x=–4.
7) уравнение плоскости A1A2A3.
Уравнение этой плоскости было найдено в п. 3).
x+4y+3z–28=0
8) уравнение высоты, опущенной из вершины A4 на грань A1A2A3.
Вектор нормали плоскости A1A2A3 будет направляющим
вектором высоты. Т.к. высота проходит через точку A4, получим ее уравнение:
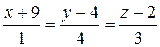
В задачах 50–60 составить уравнение геометрического места
точек, отношение расстояний которых до точки A(x,y) и прямой x=a равно числу b. Сделать чертеж.
52. A(8;0);
x=4; b=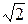
Решение.
Расстояние от точки с
координатами (x;y) до точки F с координатами
(8;0) будет равно 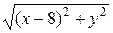
Расстояние от точки с
координатами (x;y) до прямой x=4 равно x–4.
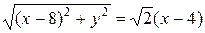
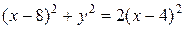
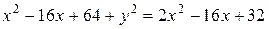
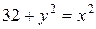
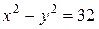
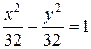
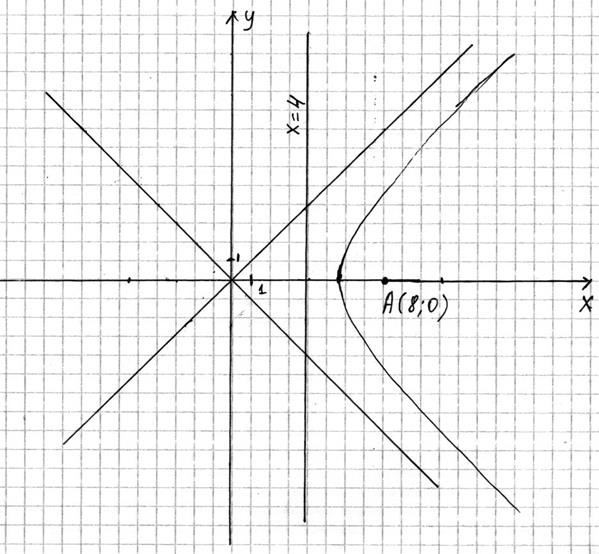
Гипербола.
В задачах 71–80 решить систему линейных уравнений методом
Крамера.
72. 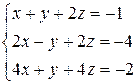
Решение.
∆ = 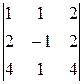 =
= 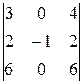 = (–1)∙
= (–1)∙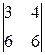 = 6.
= 6.
Т.к. ∆≠0, то система имеет единственное решение.
∆1 = 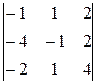 =
= 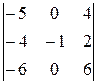 = (–1)∙
= (–1)∙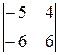 = 6.
= 6.
∆2 = 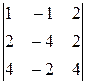 = 4∙
= 4∙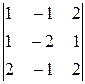 = 4∙
= 4∙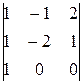 = 4∙
= 4∙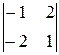 = 4∙3=12
= 4∙3=12
∆3 = 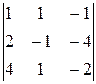 =
= 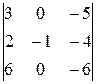 = (–1)∙
= (–1)∙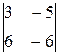 = –12
= –12
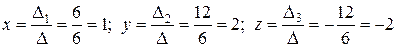
В задачах 81–100 исследовать систему линейных уравнений на
совместность и решить ее, если она совместна.
92. 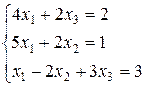
Решение.
Запишем систему в матричной форме.
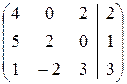 ~
~ 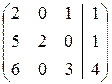 ~
~ 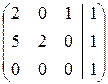
Rg A=2≠3=Rg A*, следовательно система не
совместна.
Контрольная работа № 2.
В задачах 101–120 найти пределы функций, не пользуясь
правилом Лопиталя.
112. а) 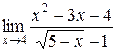 =
= 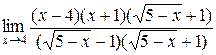 =
= 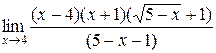 =
= 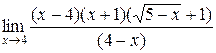 =
= 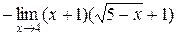 = –5∙2 = –10
= –5∙2 = –10
б) 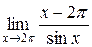 =
= 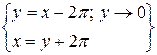 =
= 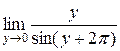 =
= 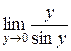 =
= 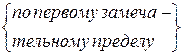 = 1.
= 1.
в) 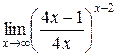 =
= 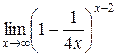 =
= 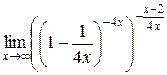 =
= 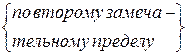 =
= 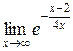 =
= 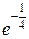
В задачах 121–140 найти производные y’.
132. а) 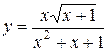
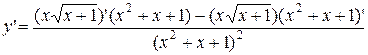 =
= 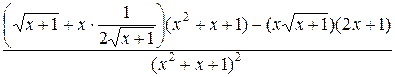 =
= 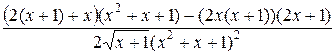 =
= 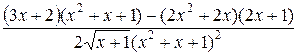 =
= 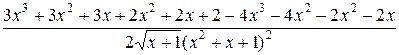 =
= 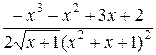
б) 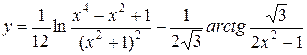
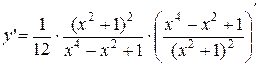 –
– 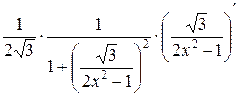 =
= 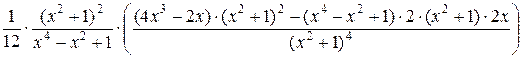 –
– 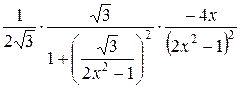 =
= 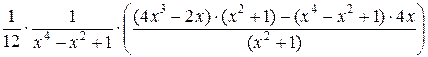 +
+ 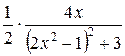 =
= 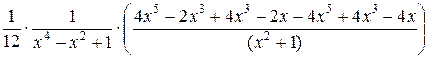 +
+ 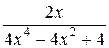 =
= 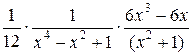 +
+ 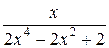 =
= 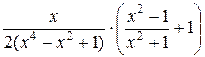 =
= 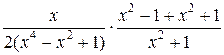 =
= 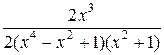 =
= 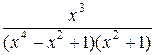
в) 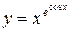
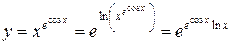
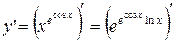 =
= 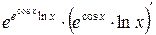 =
= 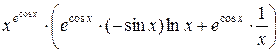 =
= 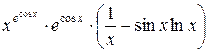
г) 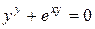
Решение.
Преобразуем выражение.
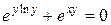
Взяв производную, получим:
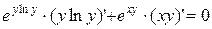
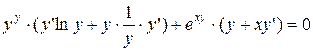
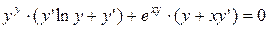
д) 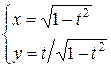
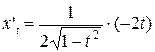 =
= 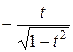
 =
= 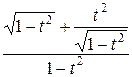 =
= 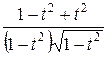 =
= 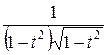
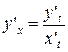 =
= 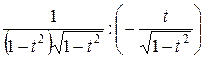 =
= 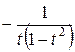
В задачах 141–160 найти приближенное значение указанных
величин с помощью дифференциалов соответствующих функций.
152. arcsin
0.4983
Решение.
Воспользуемся формулой дифференциала.
y(x) ≈ y(x0)+y’(x0)·∆x
В этих обозначениях получим:
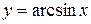
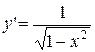
x0=0.5
x=0.4983
∆x=x–x0=–0.0017
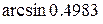 =
= 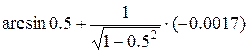 =
= 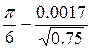 = 0.5236–0.0019 = 0.5217
= 0.5236–0.0019 = 0.5217
В задачах 161–180 исследовать данные функции методами
дифференциального исчисления и построить их графики. Исследование функции
рекомендуется проводить по следующей схеме: 1) найти область определения
функции; 2) исследовать функцию на непрерывность; 3) определить является ли
данная функция четной, нечетной; 4) найти интервалы возрастания, убывания
функции и ее точки экстремума; 5) найти интервалы выпуклости и вогнутости
графика функции и точки перегиба; 6) найти асимптоты графика функции.
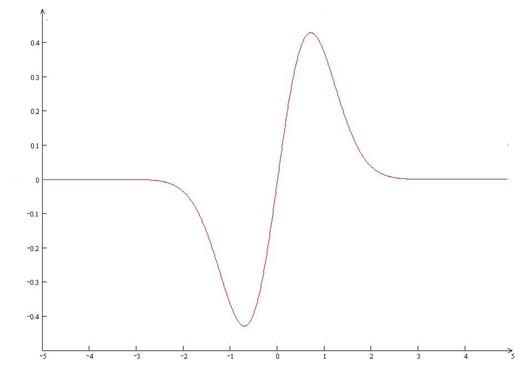
172. 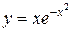
Решение.
1) Областью определения функции является вся числовая
прямая.
2) Функция является непрерывной в области определения.
3) Четность функции.
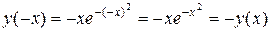 , т.е. функция нечетна.
, т.е. функция нечетна.
4) Исследуем функцию на монотонность. Для этого найдем
производную.
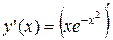 =
= 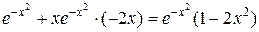
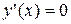
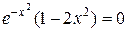
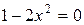
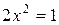
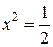
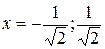
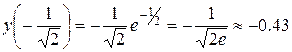
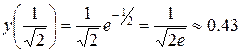
|
x
|
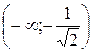
|
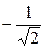
|
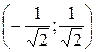
|
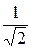
|
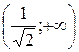
|
|
y’
|
–
|
0
|
+
|
0
|
–
|
|
y
|
↓
|
мин
|
↑
|
макс
|
↓
|
5) Исследуем функцию по второй производной.
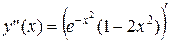 =
= 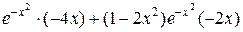 =
= 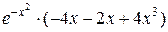 =
= 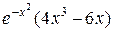
y”=0
4x3–6x=0
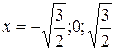
y(0)=0
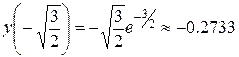
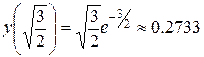
|
x
|
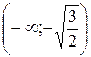
|
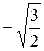
|
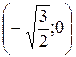
|
0
|
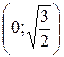
|
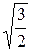
|
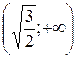
|
|
y”
|
–
|
0
|
+
|
0
|
–
|
0
|
+
|
|
y
|
выпукла
|
т.
перегиба
|
вогнута
|
т.
перегиба
|
выпукла
|
т.
перегиба
|
вогнута
|
6) Асимптоты.
а) т.к. функция непрерывна в области определения, то
вертикальных асимптот нет
б) Невертикальные. y=kx+b
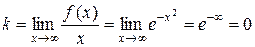
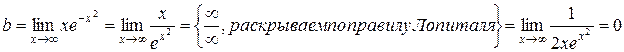
y=0 – горизонтальная
асимптота.
192. Периметр равнобедренного треугольника равен 2p. Каковы должны быть его
стороны, чтобы объем тела, образованного вращением этого треугольника вокруг
его основания был наибольшим?
Решение.
Обозначим длину боковой стороны треугольника a. Тогда длина основания
треугольника будет равна 2b=2(p–a).
Найдем объем тела, образованного вращением этого
треугольника вокруг его основания.
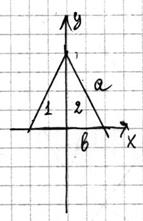
Так как объемы тел, образованными вращениями половин
треугольника, обозначенных на рисунке цифрами 1 и 2 равны, то можно найти объем
только одного тела.
Найдем объем тела, образованного вращением треугольника 1.
Уравнение гипотенузы этого треугольника будет
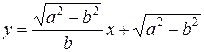
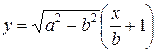
Объем тела, образованного вращением кривой y=y(x)
вокруг оси Ox равен:
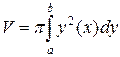
В нашем случае получим:
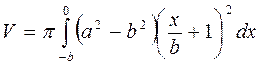 =
= 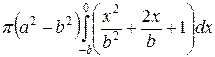 =
= 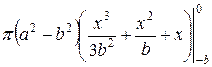 =
= 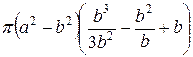 =
= 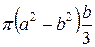
Заменив b на (p–a) получим:
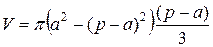 =
= 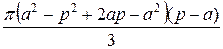 =
= 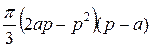 =
= 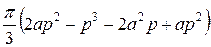 =
= 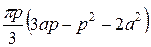
Для нахождения максимума полученной функции возьмем
производную по a.
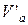 =
= 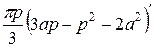 =
= 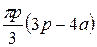
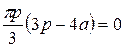
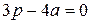
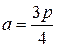
Следовательно, для достижения максимума объема необходимо,
чтобы боковая сторона треугольника была длиной 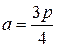
В задачах 201–220 найти неопределенные интегралы:
212. а) 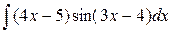 =
= 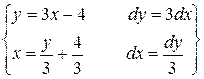 =
= 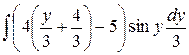 =
= 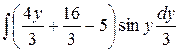 =
= 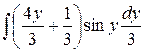 =
= 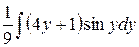 =
= 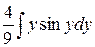 +
+ 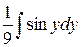 =
= 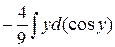 –
– 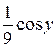 = –
= –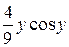 +
+ 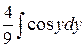 –
– 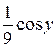 = –
= –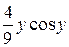 +
+ 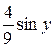 –
– 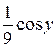 + C = –
+ C = –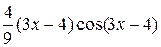 +
+ 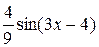 –
– 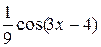 + C =
+ C = 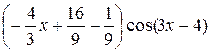 +
+ 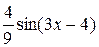 + C =
+ C = 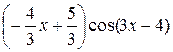 +
+ 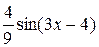 + C
+ C
б) 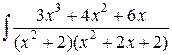
Решение.
Разложим подынтегральное выражение на простые дроби.
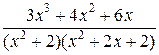 =
= 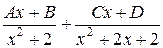 =
= 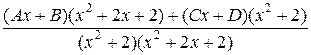 =
= 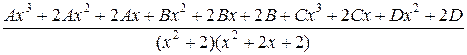
Приравнивая коэффициенты при соответствующих степенях,
получим:
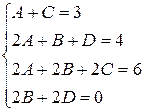
Решив систему, получим:
B=0
D=0
A=2
C=1
Таким образом получаем следующее разложение:
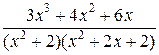 =
= 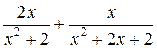
Вернемся к интегралу
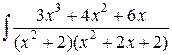 =
= 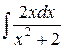 +
+ 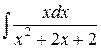
Возьмем полученные интегралы по отдельности.
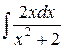 =
= 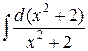 = ln(x2+2)
+ C
= ln(x2+2)
+ C
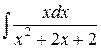 =
= 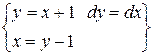 =
= 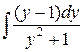 =
= 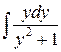 –
– 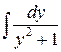 =
= 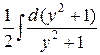 –
– 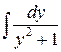 =
= 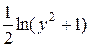 – arctg(y) =
– arctg(y) = 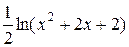 – arctg(x+1) + C
– arctg(x+1) + C
В итоге получим:
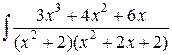 = ln(x2+2) +
= ln(x2+2) + 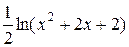 – arctg(x+1) + C
– arctg(x+1) + C
в) 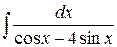 =
= 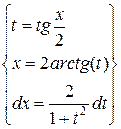 =
= 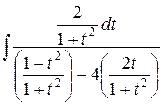 =
= 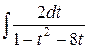 =
= 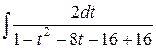 =
= 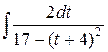 =
= 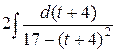 =
= 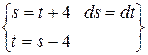 =
= 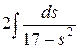 =
= 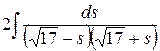 =
= 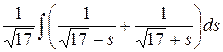 =
= 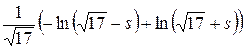 +С =
+С = 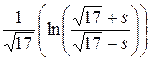 + С =
+ С = 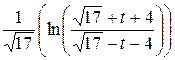 + С =
+ С = 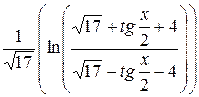 + С.
+ С.
В задачах 221–240 вычислить несобственный интеграл или
доказать его расходимость:
232. 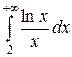 =
= 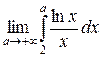 =
= 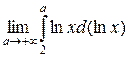 =
= 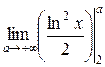 =
= 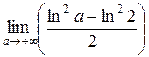 = +∞
= +∞
Следовательно, интеграл расходится.
В задачах 251–253 вычислить длины дуг кривых, заданных
уравнениями в прямоугольной системе координат.
252. 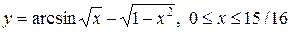
Решение.
В общем случае длина дуги кривой находится по формуле.
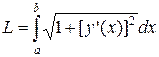
Найдем производную указанной функции.
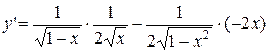 =
= 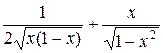
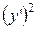 =
= 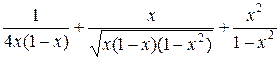 =
= 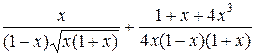 =
= 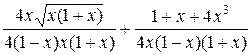 =
= 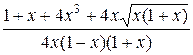 =
= 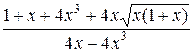
Найдем длину дуги кривой.
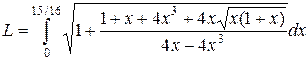 =
= 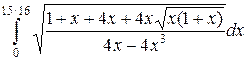
Данный интеграл не берется в элементарных функциях.
Если условие задачи поменять как
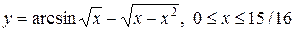
То решение выглядит следующим образом.
Найдем производную указанной функции.
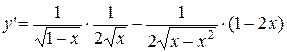 =
= 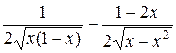 =
= 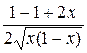 =
= 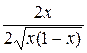 =
= 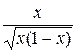
Найдем длину дуги кривой:
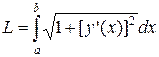 =
= 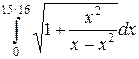 =
= 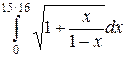 =
= 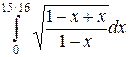 =
= 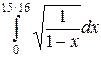 =
= 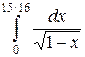 =
= 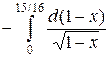 =
= 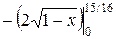 =
= 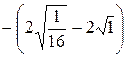 =
= 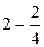 = 1.5
= 1.5