В современном научном мире статистика имеет огромное теоретическое и прикладное значение. Статистика распространила своё влияния на такие ветви научных знаний как экономика, социология, психология, биология и т.д. За время своего развития статистика разработала мощный аппарат для исследования разнообразной информации. Одним из непременных условий правильного восприятия и тем более практического использования статистической инфор­мации, квалифицированных, выводов и обоснованных решений является владение статистической методологией изучения коли­чественной стороны массовых социально-экономических явлений: знание природы статистических совокупностей, назначения и познавательных возможностей показателей статистики, условий их применения в  исследовании.

 Цель данной работы заключается в изучении теоретических основ одного из инструментов статистики, использование инструментов статистики для  анализа информации.

Для достижения  поставленной цели  были поставлены следующие задачи: дать характеристику и проиллюстрировать на примере такой инструмент статистики как мода и медиана, написать программу исследования статистической информации по таким разделам научных знаний как социология, психология и экономика труда, на основе одного из исследований вычислить коэффициенты уравнения линейной зависимости, проверить статистические гипотезы по полученному уравнению.

Задание 1. Мода и медиана – инструменты статистики

В качестве статисти­ческих характеристик вариационных рядов распределения рассчитываются так называемые структурные средние - мода и медиана.

Мода (Мо) представляет собой значение изучаемого признака, повто­ряющееся с наибольшей частотой. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины [1, стр. 184]:

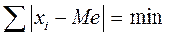
Рассмотрим определение моды и медианы по несгруппированным дан­ным. Предположим, рабочие бригады, состоящей из 9 человек, имеют сле­дующие тарифные разряды: 4,3,4,5,3,3,6,2,6.

Так как в данной бригаде больше всего рабочих 3-го разряда, этот тарифный разряд и будет модальным.

Для определения медианы необходимо провести ранжирование:

2,3,3,3,4,4,5,6,6.

Центральным в этом ряду является рабочий 4-го разряда, следователь­но, данный разряд и будет медианным. Если ранжированный ряд включа­ет четное число единиц, то медиана определяется как средняя из двух цен­тральных значений.

Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределе­ния совокупности. Проиллюстрируем ее познавательное значение следую­щим примером.

Допустим, нам необходимо дать характеристику среднего дохода груп­пы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 100 до 1000 долл. в месяц, а месячные доходы последнего составляют 50 000 долл. (табл. 7.11).

Таблица   1 Месячные доходы исследуемой группы людей

 Если мы воспользуемся средней арифметической, то получим средний доход, равный примерно 600 - 700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальной части группы. Медиана же, равная в данном случае 163 долл., позволит дать объективную характеристику уровня доходов 99 % данной группы людей.

Рассмотрим определение моды по сгруппированным дан­ным (рядам распределения). Предположим, распределение рабочих уже не отдельной бригады, а всего предприятия в целом по тарифному разряду имеет следующий вид (табл. 2).

Таблица   2 Распределение рабочих предприятия по тарифному разряду

Для определения моды по дискретному вариационному ряду необходимо определить наибольшую частоту и соответствующий разряд: 60 человек имеет 5-й тарифный разряд, следовательно, он и является модальным.

Задание 2. Программа исследований

Как уже отмечалось, выше инструменты теоретической статистики могут быть использованы для обработки данных в теоретических и практических исследованиях большого числа научных дисциплин.

Рассматриваемый эксперимент заключается в исследовании группы авиадиспетчеров, моделирующих оптимальное управление полётами для заданного типа самолета на компьютерном тренажере. Нас интересует количество ошибок, сделанных испытуемыми в зависимости от разных факторов (из сферы психологии, социологии и экономики труда) до просмотра развлекательных передач и после.

 Психология. Проводился анализ связи коли­чества ошибок, допущенных испытуемыми в тренировочной сессии, с показателями вербального и невербального интеллекта, измеренными по методике Д. Векслера. Также изучалось воздействие просмотра в течение длительного времени сериалов, ток – шоу, и других развлекательных передач на исследуемые связи. [2, стр.214] Например, в эксперименте, моделирующем деятельность авиадиспетчера, группа испытуемых, авиадиспетчеров проходила подготовку перед началом работы на тренажере. Испытуемые должны были решать задачи по выбору оптимального типа взлет­но-посадочной полосы для заданного типа самолета.

Для реализации поставленной цели были выполнены следующие действия:

·        По методике Векслера у контрольной группы авиадиспетчеров из 40 человек измерялся показатель вербального и невербального интеллекта.

·        Далее проводится эксперимент, моделирующий деятельность авиадиспетчера. Испытуемые должны решать задачи по выбору оптимального типа взлет­но-посадочной полосы для заданного типа самолета.

·        Затем проводился анализ связи коли­чества ошибок, допущенных испытуемыми в тренировочной сессии с  показателями вербального и невербального интеллекта, измеренными по методике Д. Векслера.

·        После этого испытуемые в течение 4 часов смотрят развлекательные телепрограммы.

·        Повторяются первые три пункта программы исследования.

·        Сопоставляются полученные результаты зависимостей. Делаются выводы воздействии просмотра развлекательных телепередач на количество ошибок при прохождении тестов.

Социология.  Предположим на способность управлять самолетом  до и после просмотра развлекательных передач влияет  возраст испытуемых.

·        Сначала выяснили возраст каждого из испытуемых.

·         Далее проводится эксперимент, моделирующий деятельность авиадиспетчера. Испытуемые должны решать задачи по выбору оптимального типа взлет­но-посадочной полосы для заданного типа самолета.

·        После первого теста проводился анализ связи коли­чества ошибок, допущенных в тренировочной сессии с  возрастом испытуемых.

·         Затем испытуемые в течение 4 часов смотрят развлекательные телепрограммы.

·        Повторяются первые три пункта программы исследования.

·        Сопоставляются полученные результаты зависимостей. Делаются выводы воздействии просмотра развлекательных телепередач на количество ошибок при прохождении тестов в зависимости от возраста авиадиспетчера.

Экономика труда. При изучении рынка труда авиадиспетчеров важным фактором является опыт работы. Предположим люди обладающие большим опытом работы меньше реагируют на  внешние раздражители в виде просмотра развлекательных передач.

·        Сначала узнаем из трудовой книжки опыт работы по специальности авиадиспетчера каждого из испытуемых.

·         Далее проводится эксперимент, моделирующий деятельность авиадиспетчера. Испытуемые должны решать задачи по выбору оптимального типа взлет­но-посадочной полосы для заданного типа самолета.

·        После первого теста проводился анализ связи коли­чества ошибок, допущенных в тренировочной сессии с  возрастом испытуемых.

·         Затем испытуемые в течение 4 часов смотрят развлекательные телепрограммы.

·        Повторяются первые три пункта программы исследования.

·        Сопоставляются полученные результаты зависимостей. Делаются выводы воздействии просмотра развлекательных телепередач на количество ошибок при прохождении тестов в зависимости от опыта работы авиадиспетчером.

Задание 3. Оценка регрессионной зависимости количества ошибок и уровня вербального интеллекта

По методике психологического исследования влияния просмотра развлекательных телепередач на уровень вербального и невербального интеллекта проводилось исследование эксперимент, моделирующий деятельность авиадиспетчера, группа испытуемых (40 человек), студентов физического факультета СПбГУ проходила подготовку перед началом работы на тренажере. Испытуемые должны были решать задачи по выбору оптимального типа взлет­но-посадочной полосы для заданного типа самолета. Проводился анализ связи коли­чества ошибок, допущенных испытуемыми в тренировочной сессии, с показателями вербального и невербального интеллекта, измеренными по методике Д. Векслера.

Таблица 3. Показатели количества ошибок в тренировочной сессии и показатели уровня вербального интеллекта у студентов-физиков

Построим диаграмму рассеивания зависимости количества ошибок от вербального интеллекта при моделировании деятельности авиадиспетчера.

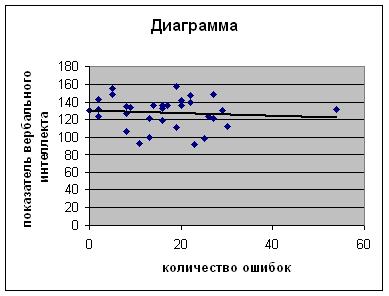
Из диаграммы и предполагаемой линии тренда можно сделать предположение о слабой зависимости между количеством ошибок и показателем вербального интеллекта.

Одной из систем корреляционной связи является линейная связь между двумя признаками — парная линейная корреляция.

Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид [4, стр.239]:

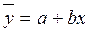
где 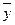 - среднее значение результативного признака у при определенном значении факторного признака х;

а - свободный член уравнения;

b - коэффициент регрессии, измеряющий среднее отношение откло­нения результативного признака от его средней величины к от­клонению факторного признака от его средней величины на одну единицу его измерения - вариация у, приходящаяся на единицу вариации х.

Уравнение регрессии определяется по данным о значениях признаков х и у в изучаемой совокупности, состоящей из n единиц. Параметры уравнения а и b находятся методом наименьших квадратов (МНК).

Исходное условие МНК для прямой линии имеет вид:

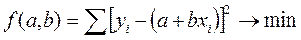
Для отыскания значений параметров а и Ь, при которых f(a,b) принимает минимальное значение, частные производные функции приравниваем нулю и преобразуем получаемые уравнения, которые называются нормальными уравнениями МНК для прямой:

 Нормальные уравнения МНК для прямой линии регрессии явля­ются системой двух уравнений с двумя неизвестными a и b. Все остальные величины, входящие в систему, определяются по расчетной информации из таблицы 3. Таким образом, однозначно вычисляются при решении этой системы уравнений оба параметра уравнения линей­ной регрессии.

Если первое нормальное уравнение разделить на n, получим:

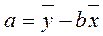
Через это уравнение обычно на практике вычисляется свободный член уравнения регрессии а. Параметр b вычисляется по преобра­зованной формуле, которую можно вывести, решая систему нормаль­ных уравнений относительно b:

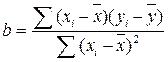
Подставим полученные значения из таблицы 3 в формулу и рассчитаем a и  b:

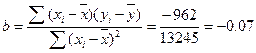
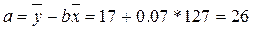
Искомая зависимость выглядит следующим образом:

Y= 26 – 0,07х

По данному уравнению можно сказать, что каждый пункт вербального интеллекта сокращает количество ошибок на 0,07.

Коэффициент парной линейной регрессии, обозначенный b имеет смысл показателя силы связи между вариацией факторного призна­ка х и вариацией результативного признака у. Он измеряет среднее по совокупности отклонение у от его средней величины при откло­нении признака х от своей средней величины на принятую единицу измерения.

При линейной форме уравнения применяется показатель тесноты связи - коэффициент корреляции r. Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных еди­ницах измерения признаков, а в долях среднего квадратического от­клонения результативного признака:

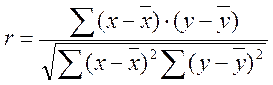
Его интерпре­тация такова: отклонение признака-фактора от его среднего значе­ния на величину своего среднего квадратического отклонения в среднем по совокупности приводит к отклонению признака-резуль­тата от своего среднего значения на г его среднего квадратическо­го отклонения.

Рассчитаем коэффициент корреляции с помощью расчетной таблицы 4.

Подставим полученные значения в формулу для расчета корреляции:

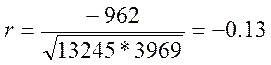
По значению коэффициента корреляции можно сказать, что связь между изучаемыми показателями довольно слабая. Но нужно проверить этот показатель на значимость.

Задание 4. Проверка статистических гипотез значимости некоторых параметров уравнения линейной парной регрессии

Показатели корреляционной связи, вычисленные по ограничен­ной совокупности (по выборке), являются лишь оценками той или иной статистической закономерности, поскольку в любом парамет­ре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необхо­дима статистическая оценка степени точности и надежности пара­метров корреляции. Под надежностью здесь понимается вероятность того, что значение проверяемого параметра не равно нулю, не вклю­чает в себя величины противоположных знаков.

Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцени­ваемой величины со средней случайной ошибкой оценки. Для ко­эффициента парной регрессии b средняя ошибка оценки вычисля­ется как:

m_b=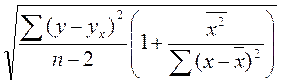   m_a=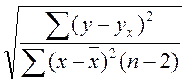

Проверим гипотезу Н₀: а=0и b=0 с помощью t- критерия. Гипотеза отвергается с вероятностью 95%, если [5, стр.84]

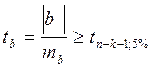  и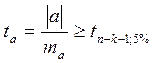  

Составим таблицу для расчетов.

t_b=0,82   t_a=2,31

t_р=2,02

Таким образом для коэффициента а мы отвергаем нулевую гипотезу,  для b принимаем.

Теснота парной линейной корреляционной связи, как и любой другой показатель, может быть измерена корреляционным отноше­нием.

Показатели тесноты связи, исчисленные по данным срав­нительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает не­обходимость проверки их существенности.

Для оценки значимости коэффициента корреляции r при­меняется t-критерий Стыодента. При этом определяется фак­тическое значение критерия t_r:

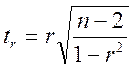
Вычисленное по формуле  значение t_r, сравнивает­ся с критическим t_k, которое берется из таблицы значений t-Стьюдента с учетом заданного уровня значимости аи чис­ла степеней свободы.

Если t_r > t_k, то величина коэффициента корреляции при­знается существенной.

В нашем случае:

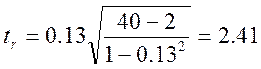
t_k=2

t_r > t_k следовательно отвергаем нулевую гипотезу о незначимости связи х и у.

Важным этапом корреляционного анализа связи является оценка практической значимости синтезированных моделей. Смысл такой оценки состоит в том, чтобы обосновать приме­нение метода функционального анализа при изучении корре­ляционной зависимости. Правомерность такого приема ана­лиза будет оправданной лишь в тех случаях, если изучаемая корреляционная связь не столь значитель­но отстоит от функциональной связи. При этом не­обходимо доказать, что применение метода функционально­го анализа при изучении корреляционной зависимости не дает существенных погрешностей. [6, стр. 340]

Проверка практической значимости синтезированных в корреляционно-регрессионном анализе математических моде­лей осуществляется посредством показателей тесноты связи между признаками х и у.

Для статистической оценки тесноты связи применяются следующие показатели:

Соотношение между факторной 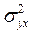 и общей  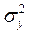диспер­сиями характеризует меру тесноты связи между признаками х  и у.

Показатель R² называется коэффициентом детерминации. Он выражает долю факторной дисперсии в общей дисперсии, т.е. характеризует, какая часть общей вариации результативного признака у объясняется изучаемым факто­ром х. В нашем примере фактор вербального интеллекта объясняет 1,7% дисперсии количества ошибок на тренажере.

Для оценки значимости коэффициентом детерминации применя­ется критерий Фишера.

Фактическое значение критерия F_р для линейной парной регрессии определяется по формуле:

Fр=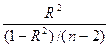

Величина F_R сравнивается с критическим значением F_k, которое определяется по таблице F-критерия с учетом приня­того уровня значимости а и числа степеней свободы к_х =1 и к_г= п - 2.

Если F_R > F_k, то гипотеза о существенности величины коэффициента детерминации принимается.

Fр=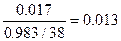 Fk=250

Значение коэффициента детерминации не значимо.  Полученное уравнение регрессии показывает слабую взаимосвязь между уровнем вербального интеллекта и количеством допущенных ошибок в эксперименте моделирующем деятельность авиадиспетчера.

Заключение

В заключении хотелось бы еще раз отметить большую теоретическую и практическую значимость статистики для других наук. В этой работе было продемонстрировано на примере  написания программы исследований, что инструменты статистики можно использовать для анализа воздействия просмотра развлекательных передач на количество ошибок при прохождении теста авиадиспетчерами с точки зрения трех дисциплин: психологии, социологии и экономики труда.

Более подробно была рассмотрена часть психологического исследования, которое заключалось в эксперименте, моделирующем деятельность авиадиспетчера, группа испытуемых авиадиспетчеров проходила подготовку перед началом работы на тренажере. Испытуемые должны были решать задачи по выбору оптимального типа взлет­но-посадочной полосы для заданного типа самолета. Проводился анализ связи коли­чества ошибок, допущенных испытуемыми в тренировочной сессии, с показателями вербального и невербального интеллекта, измеренными по методике Д. Векслера. Проведенный анализ выявил слабую взаимосвязь этих показателей.

Практическая значимость проведенного исследования заключается в том, что при приёме на работу авиадиспетчеров уровень вербального интеллекта не является решающим фактором.

Также в работе были описаны и проиллюстрированы на примере такие инструменты статистики как мода и медиана.

Литература

1. Теория статистики: Учебник/ Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 1996. – 464 с.

2. Сидоренко Е.В. Методы математической обработки в психологии. СПб.: СПбГУ, 2000. – 367 с.

3.  Практикум по социальной статистике: Учебник/ Под ред. чл.-кор. РАН И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 494 с.

4. Общая теория статистики: Учебник/ под ред. чл.-корр. РАН И.И. Елисеевой. – М.: Финансы и статистика, 1999. – 484 с.

5. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 2001. – 402с.

6. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник/ под ред. О.Э. Башиной, А.А. Спирина.- М.: Финансы и статистика, 1999. – 440 с.