Контрольная работа № 1

1)     Вычислить определитель матрицы  С=А² + 3А – Е разложением по второй строке, где 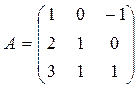 , Е – единичная матрица. Являются ли столбцы матрицы С линейно независимыми?

РЕШЕНИЕ:

     

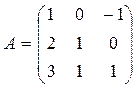
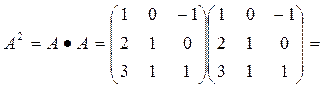
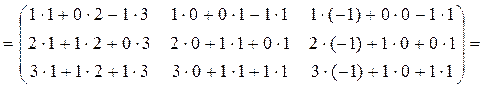
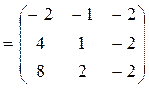
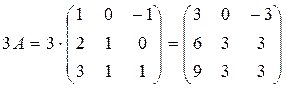
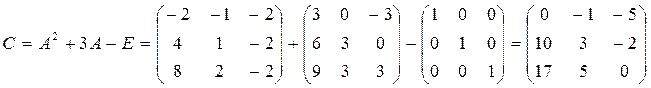
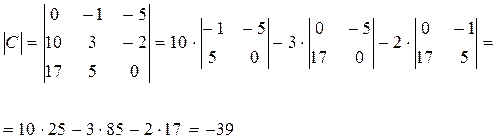
     Поскольку , то столбцы матрицы С являются линейно независимыми.

2) Найти предел: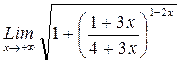

РЕШЕНИЕ:

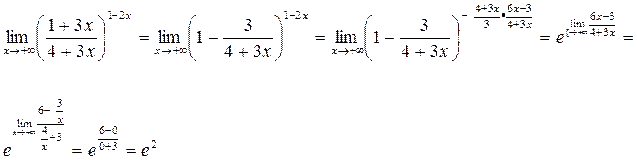
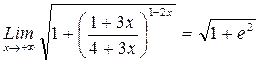
3) Найти производную функции: 

РЕШЕНИЕ:

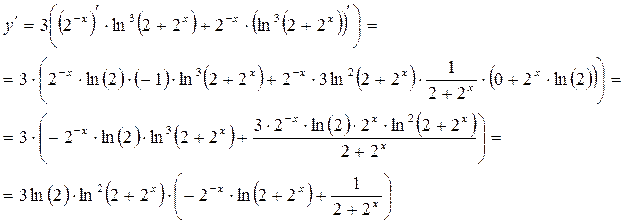
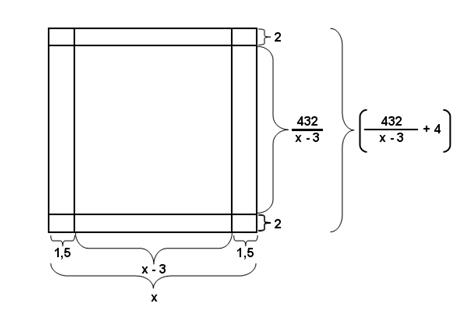
4) Площадь, занимаемая печатным текстом, составляет на странице книги 432 см². Ширина полей вверху и внизу страницы составляет 2 см., а ширина боковых полей по 1,5 см. Каковы должны быть ширина и высота страницы, чтобы количество израсходованной бумаги было наименьшим?

РЕШЕНИЕ:

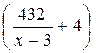     Пусть х – ширина страницы, тогда (х-3) – ширина печатной страницы. Поскольку площадь печатной площади равна 432 (см²), то значит высота печатной площади равна см., а высота страницы равна см.

Тогда количество израсходованной бумаги равно 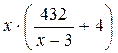см²

     Пусть f(x) – количество израсходованной бумаги. Найдём минимум f(x) с помощью производной.

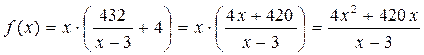
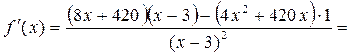
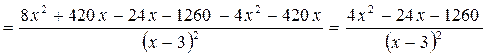
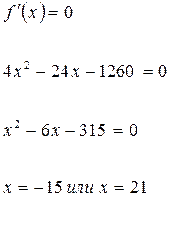
не подходит, т. к. отрицательное число см. ширина страницы. Тогда высота страницы равна

5) Составить уравнения касательных к графику функций , перпендикулярных прямой, пересекающейся с осью в точке  и с осью в точке . Сделать чертеж.

РЕШЕНИЕ:

     Найдём уравнение прямой, пересекающейся с осью в точке , а с осью в точке .

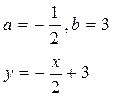
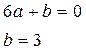
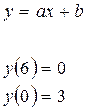
Эта прямая имеет угловой коэффициент:

Значит управления касательных к графику будут иметь угловой коэффициент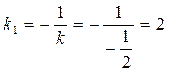

Найдём точки на графике функции , в которых угловой коэффициент равен 2, т. е. такие, где

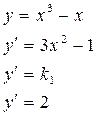
Напишем уравнения касательных:

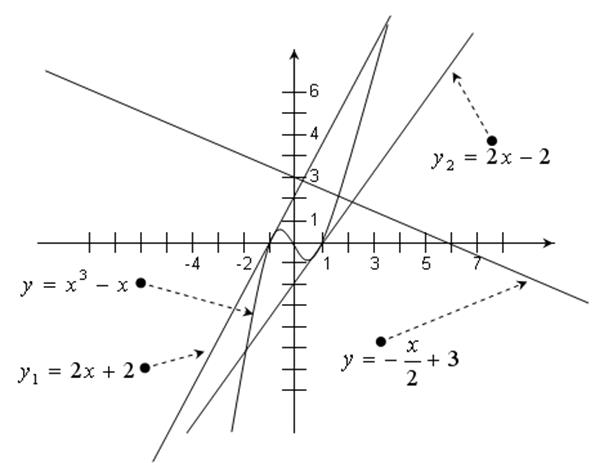
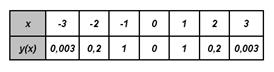
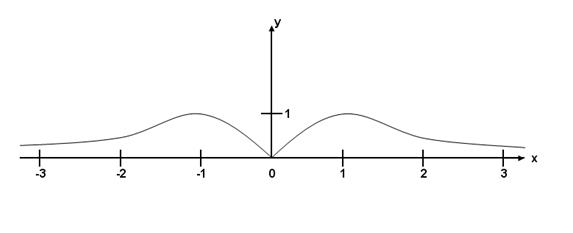
6) Исследовать функцию и схематично построить её график.

РЕШЕНИЕ:

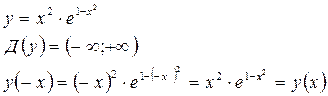
Значит  - чётная  функция и график симметричен относительно оси ,

 - не периодична, т. к.  не содержит тригонометрических функций

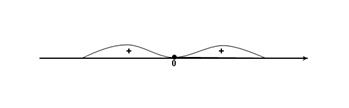
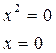
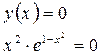
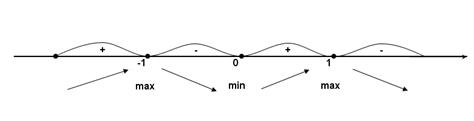
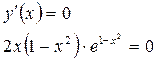
 или

 или

- точки перегибов

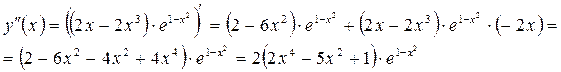
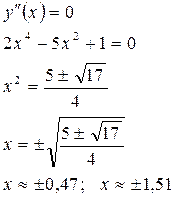
Найдём асимптоты:

Вертикальных асимптот нет, т. к. нет точек разрыва.

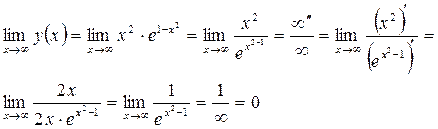
Значит - горизонтальная асимптота, при

Наклонных асимптот нет, поскольку есть горизонтальная.