Контрольная работа № 4.
№ 1. Найти
неопределенные интегралы. Правильность полученных результатов проверить
дифференцированием.
1) 
= 
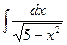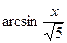+ C.
Проверка.
= 
= 
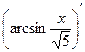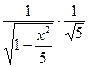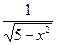
2) 
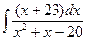
Преобразуем
подынтегральное выражение.
= 
= 
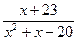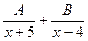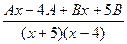
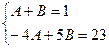
A=1–B
–4(1–B)+5B=23
–4+4B+5B=23
9B=27
B=3
A=1–3=–2
В итоге получаем:
= 
= 
– 
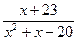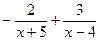
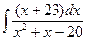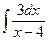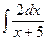= 3ln|x–4|–2ln|x+5|+C
Проверка.
(3ln|x–4|–2ln|x+5|)’
= 
= 
= 
=
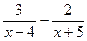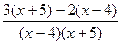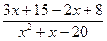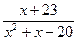
3) 
= 
= 
= 
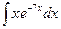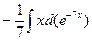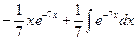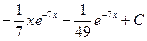
Проверка.
= 
= 
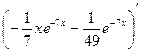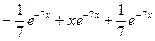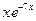
№ 2. Вычислить определенный
интеграл.
= 
= 
= 
= 
= 
= 
– 
= 
– 
= 
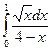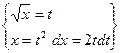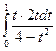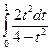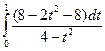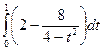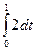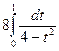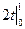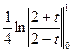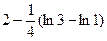= 2 –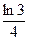 
= 1.725
№ 3. Вычислить несобственный
интеграл или установить его расходимость.
= 
= 
= 
= 
= 
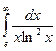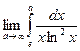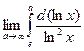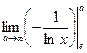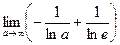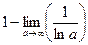= 1.
№ 4. Вычислить
площадь фигуры, ограниченной заданными кривыми. Сделать чертеж области.
2x+3y2=0; 2x+2y+1=0.
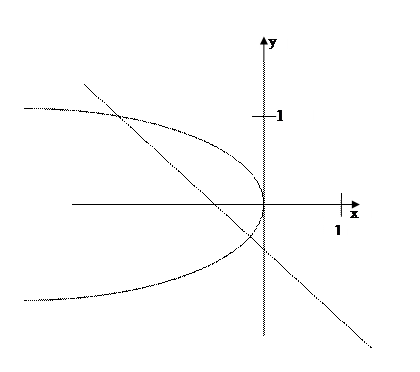
Найдем точки
пересечения графиков.
3y2=2y+1
3y2–2y–1=0
= 
= 
= 
= 
= 
= 
= 
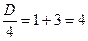
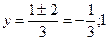
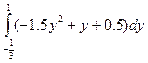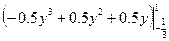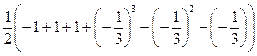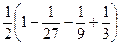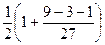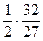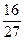
№ 5. Вычислить объем тела,
образованного вращением вокруг оси Ox кривой L.
x2+2y=0; x=1; y=0
Решение.
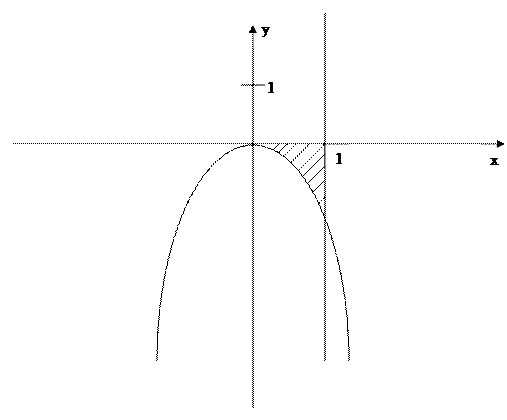
V=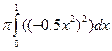
= 
= 
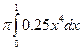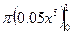= 0.05π
Контрольная работа № 5.
1. Изменить порядок
интегрирования в двойном интеграле. Сделать чертеж области интегрирования.
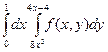
Решение.
= 
+ 
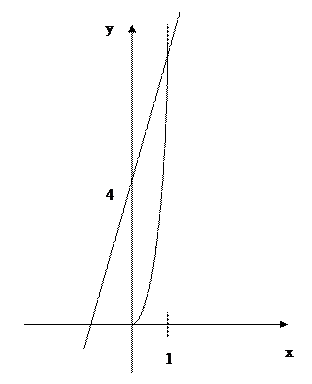
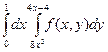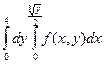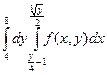
2. А. Вычислить объем тела,
ограниченного заданными поверхностями. Сделать чертеж.
x2+y2=4; y–2z+4=0; z=0
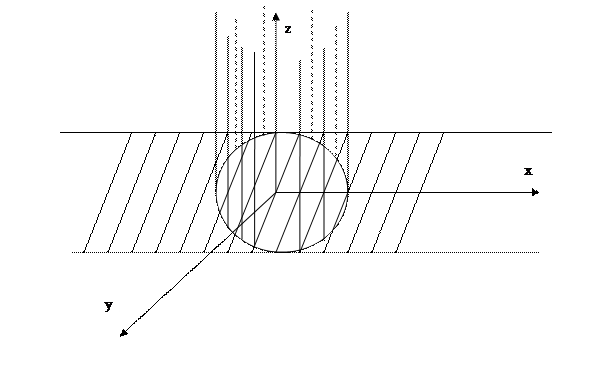
Перейдем к
цилиндрическим координатам. Получим следующие значения параметров:
0≤r≤2
0≤φ≤2π
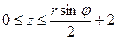
Объем тела будет равен:
V =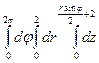 
= 
= 
= 
= 
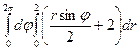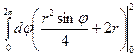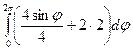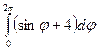= 8π
3. А.
Требуется: 1) найти поток векторного поля a через замкнутую поверхность σ = σ1 + σ2 (выбирается внешняя
нормаль к σ); 2)
вычислить циркуляцию векторного поля a по контуру Г, образованному
пересечением поверхностей σ1
и σ2
(направление обхода должно быть выбрано так, чтобы область, ограниченная
контуром Г оставалась слева); 3) проверить правильность вычисленных значений
потока и циркуляции с помощью формул Остроградского и Стокса; 4) дать
заключение о наличии источников и стоков внутри области, ограниченной
поверхностью σ; 5)
сделать схематический чертеж поверхности σ.
a=(3x+2y)i+(5x–2y)j+(3z–y2–3)k;
σ1: x2+y2=(z–1)2; σ2:
z=3.
Решение.
1) Поток поля
через замкнутую поверхность σ1
+ σ2
П = П1+П2
= 
+ 
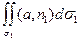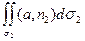
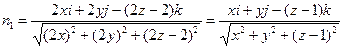
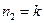
П1
= 
= 
= 
= 
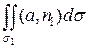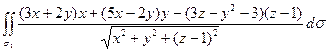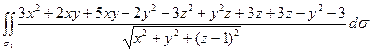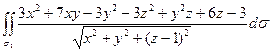
Перейдем к
координатам z, φ.
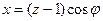
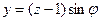
П1
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
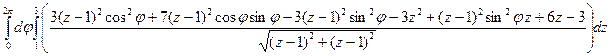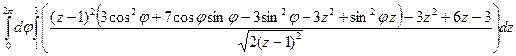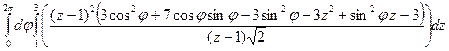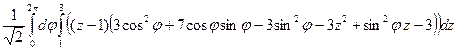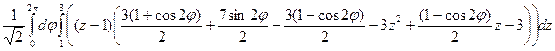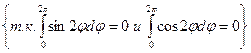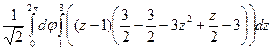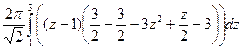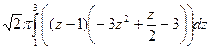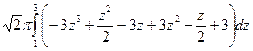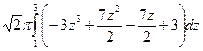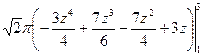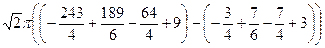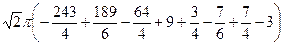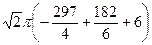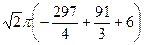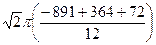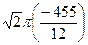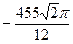
П2
= 
= 
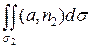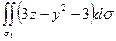
Перейдем к
полярным координатам:
z=3
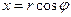
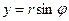
П2
= = 
= 
= 
= 
= 
= 
= 
= 
= 
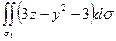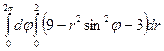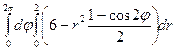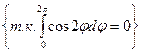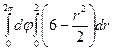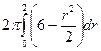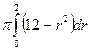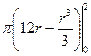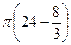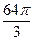
П = П1+П2
= – 
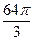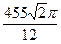
2) Ц =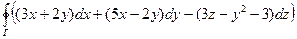 
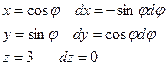
Ц =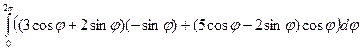 
= 
= 
= 
= = 
= 
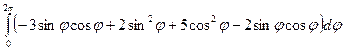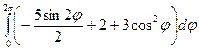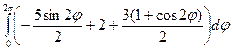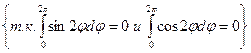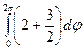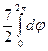= 7π
3) div a = 3 – 2 + 3 = 4.
= 
= 
= 
= 
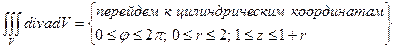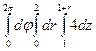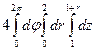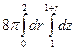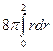= 16π
rot a =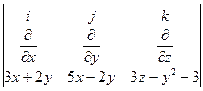 
= (–2y)i + (5–2)k = –2yi+3k
= 
= 
= 
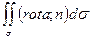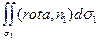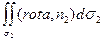
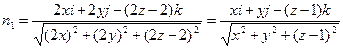
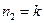
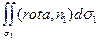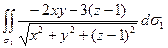
Перейдем к
координатам z, φ.
= 
= 
= 
= 
= 
= 
= 
= 
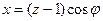
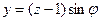
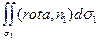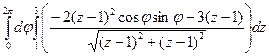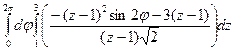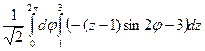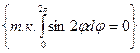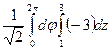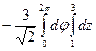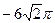
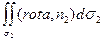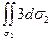
Перейдем к
полярным координатам:
z=3
= 
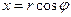
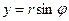
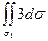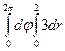= 12π
= 
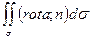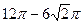
4) Т.к. div a = 4, то внутри области
имеются источники, плотность которых если принять ее непрерывной, равна 4.
5) Чертеж.
