Задание 1.

Взята ссуда на 10 лет в сумме 25000 (у.д.е.) под 25 процентов годовых, начисляемых на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года (начисление процентов совпадает со временем возврата). Требуется: составить модель погашения ссуды; вычислить величину годового платежа; определить величину всей возвращаемой суммы и величину общей суммы процентного платежа; сравнить данный вариант с вариантом возврата ссуды вместе с процентами в конце срока операции.

Решение.

Год	Возвращаемая часть долга	Проценты	Итого оплата
1	2500	25000·0.25=6250	8750
2	2500	22500·0.25=5625	8125
3	2500	20000·0.25=5000	7500
4	2500	17500·0.25=4375	6875
5	2500	15000·0.25=3750	6250
6	2500	12500·0.25=3125	5625
7	2500	10000·0.25=2500	5000
8	2500	7500·0.25=1875	4375
9	2500	5000·0.25=1250	3750
10	2500	2500·0.25=625	3125
Итого	25000	34375	59375

Если возвращать ссуду с процентами в конце срока операции, то платить  придется 25000·1.25¹⁰ = 232830.64 руб.

Задание 2.

Определить будущую стоимость обыкновенного аннуитета накопления с реальной доходностью 20 процентов в год с учетом инфляции (ежегодный темп инфляции составляет 15 процентов), если ежегодный вклад пренумерандо 1700 (у.д.е.), а срок операции 7 лет.

Указание. Наращение производить по номинальной процентной ставке, исчисленной по формуле Фишера.

Решение.

Найдем значение номинальной ставки процентов

r=0.2+0.15+0.2·0.15 = 0.35+0.03 = 0.38 = 38%

Искомая стоимость будет равна.

1700·(1.38+1.38²+1.38³+1.38⁴+1.38⁵+1.38⁶+1.38⁷) = 1700·(1.38⁸–1.38)/0.38 = 52669.75 у.д.е.

Задание 3.

Финансовый инструмент (актив) генерирует ежегодно постнумерандо в течение 5 лет постоянную сумму CF=2500 (у.д.е.).

Реальная (приемлемая) доходность 10 процентов в год, ежегодный коэффициент риска Т_риска=0.1. Определить номинальную (необходимую) ежегодную ставку дисконтирования с учетом фактора риска и современную (приведенную) стоимость данного аннуитета.

Решение.

Найдем значение номинальной (необходимой) ежегодной ставки дисконтирования с учетом фактора риска

r=1.1·1.1–1 = 0.21 = 21%

Современная (приведенная) стоимость данного аннуитета

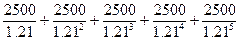 = 7314.96 у.д.е.

Задание 4.

Предприятие рассматривает инвестиционный проект, первоначальные инвестиции по которому I₀=20000 (у.д.е.). Ожидается, что реализация проекта в течение 5 лет обеспечит получение чистого дохода по годам постумерандо в объемах (у.д.е.): CF₁=7000, CF₂=9000, CF₃=12000, CF₄=11000, CF₅=8000. Принятая ежегодная норма (ставка) дисконта d=15 процентов постоянна в течение всех лет экономической жизни проекта. Требуется: 1) оценить экономическую эффективность проекта, вычислив NPV, PI; 2) сравнить данный проект с альтернативным, у которого I_а=30000, NPV_а=7250, а срок экономической жизни тоже 5 лет.

Решение.

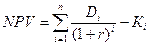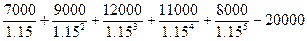 =  = 11049.14 у.д.е.

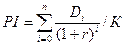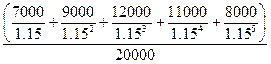 =  = 1.5525

Поскольку NPV>0 и PI>1, то проект имеет право на существование, а что касается сравнения двух проектов, то поскольку у первого проекта NPV больше, то он более выгоден, т.к. при меньших затратах обещает большую прибыль.

Задание 5.

Корпорации предлагается сформировать инвестиционную программу из шести проектов на четыре года при условии, что инвестиционные затраты по годам превышают установленный лимит средств (возможности корпорации по инвестированию ограничены). Корпорация имеет высокий финансовый рычаг и не планирует привлекать заемные средства. Рассматриваемые шесть проектов независимы и имеют тот же класс (уровень) риска, что и текущая деятельность корпорации. Проекты реализуются в объеме не более одного раза, а при необходимости могут реализоваться (инвестироваться) частично, при этом эффект, выраженный NPV, пропорционален доле реализации каждого проекта. Данные по затратам (инвестированию проектов по годам), лимит капитала b_i и NPV_j приведены в таблице:

Годы	Инвестиционные затраты по проектам (у.д.е.)	Лимит капитала (bi) по годам (у.д.е.)
1	2	3	4	5	6
1	250	50	260	160	110	90	650
2	270	250	150	200	90	110	700
3	50	110	100	50	100	350	550
4	80	90	50	90	250	50	450
NPVj	200	250	260	180	200	220

Требуется: 1) составить экономико-математическую модель задачи максимизирующей суммарный NPV; 2) решить ее симплексным методом на персональном компьютере; 3) произвести анализ результатов решения и чувствительность модели на изменение параметров.

Студенты заочной формы обучения выполняют в контрольной работе только первую часть этого задания, т.е. составляют экономико-математическую модель задачи, а вторую и третью части выполняют во время экзаменационной сессии на практических и лабораторных занятиях.

Решение.

Экономико-математическая модель задачи имеет следующий вид:

z=200x₁+250x₂+260x₃+180x₄+200x₅+220x₅→max

250x₁+50x₂+260x₃+160x₄+110x₅+90x₆≤650

270x₁+250x₂+150x₃+200x₄+90x₅+110x₆≤700

50x₁+110x₂+100x₃+50x₄+100x₅+350x₆≤550

80x₁+90x₂+50x₃+90x₄+250x₅+50x₆≤450

0≤x_i≤1, i=1..6

Задание 6.

В задачах 0-9 приведены модели, описывающие зависимость некоторого финансового показателя от нескольких факторов. Требуется при помощи методов предельного анализа: частной производной и коэффициента эластичности произвести анализ чувствительности показателя на изменение факторов при конкретных значениях факторов.

5. 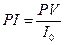 - модель вычисления индекса рентабельности инвестиционного проекта (2.3). Проанализировать изменение PI при изменении: 1) PV – современной (приведенной) стоимости проекта; 2) I₀ – первоначальных инвестиционных затрат, если PV=7000 (у.д.е.), I₀=5000 (у.д.е.).

Решение.

PI при PV=7000 (у.д.е.), I₀=5000 (у.д.е.) равен 7000/5000 = 1.4

1) Найдем частную производную.

Это обозначает, что при PV=7000 (у.д.е.), I₀=5000 (у.д.е.) при увеличении (уменьшении) PV на единицу PI увеличится (уменьшится) на 1/5000 = 0.0002

Найдем коэффициент частной эластичности E_PV(PI)

E_PV(PI)=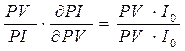 = 1

Следовательно, увеличение (уменьшение) PV на один процент приведет к увеличению (уменьшению) PI на 1 процент.

2) Найдем частную производную.

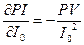
Это обозначает, что при PV=7000 (у.д.е.), I₀=5000 (у.д.е.) при увеличении (уменьшении) I₀ на единицу PI уменьшится (увеличится) на 7000/5000² = 0.00028

Найдем коэффициент частной эластичности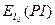

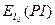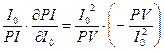 =  = –1

Следовательно, увеличение (уменьшение) I₀ на один процент приведет к уменьшению (увеличению) PI на 1 процент.

Задание 7.

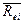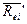Используя модель САРМ и формулу расчета стоимости (цены) акции компании i, произвести вычисления  и Р_О, а также  и 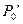 по следующим данным:

Первоначальные значения	Новые значения
Номер варианта	Rf (%)	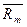(%)	βi	qi	Di	Rf’ (%)	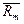’ (%)	βi’	qi’	Di’
5	9	14	0.9	0.03	2	7	13	0.8	0.02	2

Построить график модели рынка по первоначальным значениям, определить премии за риски.

Решение.

Общий вид модели САРМ.

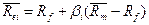
Подставив значения, получим

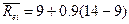=15.3

Стоимость акций в первоначальном значении

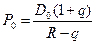
Подставив значения, получим

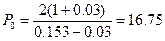
Для новых значений получим:

Общий вид модели САРМ.

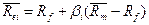
Подставив значения, получим

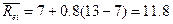
Стоимость акций в новом значении

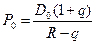
Подставив значения, получим

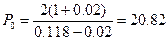
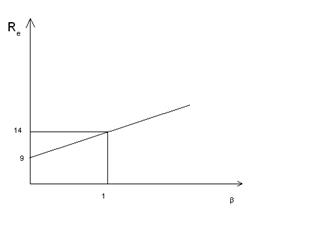
Премия за риск равна 20.82–16.75=4.07

Задание 8.

На эффективном рынке известны доходность безрисковых активов R_f=0.10, доходность рыночного портфеля (рынка) 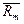=0.15, β-коэффициенты i активов доступных для выбора на рынке: β₁=0.80, β₂=0.90, β₃=1.00, β₄=1.10, β₅=1.20. Кроме того, известно предельное (сверху) значение β-коэффициента портфеля активов β_р=1.05, определенное инвестором, желающим иметь портфель максимальной доходности (выделяемые инвестором средства должны быть полностью инвестированы). Заданы дополнительно следующие условия: доля первого актива в портфеле должна быть не менее 0.25; сумма долей второго и третьего активов должна быть равна 0.35; доля четвертого актива не должна превышать 0.55, а доля пятого актива не должна превышать 0.15. Требуется: 1) рассчитать по модели САРМ ожидаемые доходности всех пяти активов; 2) построить экономико-математическую модель задачи, максимизирующей доходность портфеля, сформированного из данных активов при заданных ограничениях; 3) решить задачу оптимизации портфеля симплексным  методом; 4) произвести анализ результатов решения и чувствительность модели на изменение параметров.

Студенты заочной формы обучения выполняют только пункты 1) и 2) задания 8, остальные пункты этого задания выполняют во время экзаменационной сессии на практических и лабораторных занятиях.

Решение.

1) Общий вид модели САРМ.

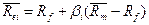
Для первого актива

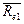 = 0.1+0.8(0.15–0.1) = 0.1+0.8·0.05 = 0.5

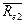 = 0.1+0.9(0.15–0.1) = 0.1+0.9·0.05 = 0.55

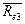 = 0.1+1.0(0.15–0.1) = 0.1+1.0·0.05 = 0.6

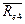 = 0.1+1.1(0.15–0.1) = 0.1+1.1·0.05 = 0.65

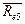 = 0.1+1.2(0.15–0.1) = 0.1+1.2·0.05 = 0.7

Обозначим x_i – доля i-ого актива в портфеле.

Получим следующую экономико–математическую модель.

0.5x₁+0.55x₂+0.6x₃+0.65x₄+0.7x₅→max

0.8x₁+0.9x₂+x₃+1.1x₄+1.1x₅≤1.05

0≤x_i≤1

x₁+x₂+x₃+x₄+x₅=1

x₁≥0.25

x₂+x₃=0.35

x₄≤0.55

x₅≤0.15

Задание 9.

Предположим, что денежные расходы компании в течении года составляют V=300000 (у.д.е.); приемлемый и возможный для компании процентный доход по краткосрочным ликвидным ценным бумагам r=0.12, расходы по конвертации (трансформированию) ценных бумаг в денежные средства c=120 (у.д.е.). Рассчитать, пользуясь моделью Баумоля–Тобина, сумму разового пополнения Q^*, количество сделок по конвертации в год, общие расходы по реализации такой политики (OP); прокомментировать политику управления денежными средствами.

Решение.

Оптимальная сумма разового пополнения определяется по формуле:

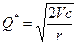
Подставив значения, получим:

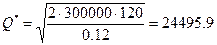
Количество сделок по конвертации в год составит k=V:Q^*=300000:24495.9=12.2, т.е. 12 сделок в год. Общие расходы по реализации такой политики управления денежными средствами составят:

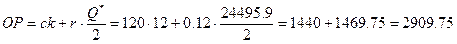
Полученные данные говорят о том, что конвертацию ценных бумаг в денежные средства при заданных условиях целесообразно проводить 12 раз в год. Оптимальная сумма пополнения равна 24495.9 у.д.е.

Задание 10.

Предположим, что минимальный ежедневный остаток денежных средств компании в объеме Q_н=1000 (у.д.е.), дисперсия ежедневных денежных потоков σ²=45000, процентная ставка (норма доходности по высоколиквидным ценным бумагам) r=0.0003 в день, расходы по конвертации (операционные издержки по продаже ценных бумаг) c=30 (у.д.е.). Рассчитать, пользуясь моделью Миллера–Орра, размах вариации R, верхний предел остатка денежных средств Q_в, точку возврата Q^*, прокомментировать политику управления денежными средствами компании.

Решение.

Размах вариации остатка денежных средств рассчитывается по формуле:

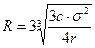
Подставив значения, получим:

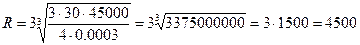
Верхняя граница остатка денежных средств равна

Q_B=Q_Н+R=1000+4500=5500

Точка возврата равна

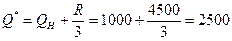
Полученные данные говорят о том, что оптимальной инвестиционной политикой компании в предлагаемых условиях будет следующая: если остаток денежных средств в некоторый момент времени достигает 5500 у.д.е., то денежные средства инвестируются в высоколиквидные активы в сумме 3000 у.д.е. При снижении остатка денежных средств до 1000 у.д.е., активы реализуются в количестве 1500 у.д.е.