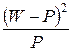Вариант 6.
Задача 1.
Из статистики деятельности биржи известно, что в среднем
цены на 65% котирующихся на бирже акций в течение месяца повысятся или
останутся неизменными, а цены на 35% акций упадут. Некто имеет 7 акций,
котирующихся на данной бирже. Определить вероятность того, что: а) более
половины имеющихся у него акций не упадут в цене; б) по крайней мере, одна
акция упадет в цене.
Решение.
а) Воспользуемся интегральной формулой Лапласа.
= 
= 
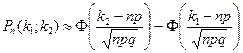
= Ф(1.51)–Ф(–0.44) =
Ф(1.51)+Ф(0.44) = 0.4345+0.17 = 0.6045 = 60.45%
б) Найдем вероятность дополнительного события. Оно будет
заключатся в том, что все акции не упали в цене.
Воспользуемся локальной формулой Лапласа.
= 
= 
= 
= 
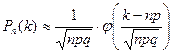
= 0.1011 =
10.11%
Вероятность искомого события равна 1–0.1011=0.8989 = 89.89%
Задача 2.
Вероятность выхода из строя изделия во время его испытания
на надежность равна 0.02. Определить вероятность того, что при испытании 210
таких изделий выйдут из строя: а) не менее одного изделия; не более одного
изделия.
Решение.
а) Найдем вероятность события дополнительного к искомому.
Оно будет заключатся в том, что ни одно изделие при испытаниях не вышло из
строя.
Воспользуемся локальной формулой Лапласа.
= 
= 
= 
= 
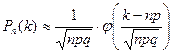
= 0.023 = 2.3%
Вероятность искомого события – 1–0.023 = 97.7%
б) Разобьем искомое событие на два: ни одно изделие не вышло
из строя, одно изделие вышло из строя. Эти события независимы и поэтому
вероятность искомого события будет равна сумме вероятностей каждого из этих
событий. Вероятность первого события найдена в пункте а) и составляет 0.023.
Найдем вероятность второго события.
= 
= 
= 
= 
= 0.0564 =
5.64%
Вероятность искомого события равна
0.023+0.0564 = 0.0794 = 7.94%
Задача 3.
Выборочным путем по схеме случайной бесповторной выборки
получены следующие данные об урожайности корнеплодов на площади 285 га из
общего массива в 2000 га:
|
Урожайность
(ц/га)
|
14–16
|
16–18
|
18–20
|
20–22
|
22–24
|
24–26
|
26–28
|
Всего
|
|
Количество
(га)
|
16
|
32
|
75
|
63
|
45
|
17
|
37
|
285
|
Определить выборочную долю площади, урожайность которой не
менее 22 ц/га и границы, в которых с вероятностью 0.9 заключена доля площади с
урожайностью не менее 22 ц/га на всем массиве.
Решение.
По выборке доля площади с урожайностью не менее 22 ц/га
равна (45+17+37)/285 = 99/285 = 0.3439 = 34.39
Для вероятности p=0.9 коэффициент доверия t=1.645 (n=285;
N=2000). Найдем
предельную ошибку при данных условиях.
m=99;n=285;w=m/n=0.3439
= 
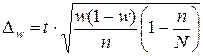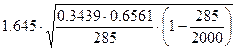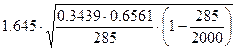= = 0.0429
Искомые границы с вероятностью 0.9 равны
(0.3439–0.0429;0.3439+0.0429)
(0.301;0.3868)
Задача 4.
В таблице приведены результаты измерений диаметра валика (в
микронах), обработанных на станке.
|
Диаметр
валика (мк)
|
5–10
|
10–15
|
15–20
|
20–25
|
25–30
|
Всего
|
|
Количество
деталей
|
55
|
95
|
120
|
70
|
60
|
400
|
Используя критерий «хи-квадрат» Пирсона, проверить гипотезу
о согласии с законом нормального распределения диаметра валика, приняв уровень
значимости равным 0.01.
Решение.
Найдем параметры распределения – среднее значение и
дисперсию.
= 
= 
= 17.3125
Дисперсия.
+ 
= 
= 39.0273437275
Среднеквадратичное отклонение.
Таблица относительных частот середин интервалов:
7.5 – 55/400 = 0.1375
12.5 – 95/400 = 0.2375
17.5 – 120/400 = 0.3
22.5 – 70/400 = 0.175
27.5 – 60/400 = 0.15
Найдем вероятности:
P(X<10)=0.5+
= 0.5+Ф(–1.17)
= 0.5– Ф(1.17) = 0.5–0.379 = 0.121
P(10<X<15) = 
– = Ф(–0.37) –
Ф(–1.17) = Ф(1.17) – Ф(0.37) = 0.379–0.1443 = 0.2347
P(15<X<20) = 
– = Ф(0.43) –
Ф(–0.37) = Ф(0.43) + Ф(0.37) = 0.1664+0.1443 = 0.3107
P(20<X<25) = 
– = Ф(1.23) –
Ф(0.43) = 0.3907–0.1664 = 0.2243
P(X>25)=0.5– = 0.5– Ф(1.23) = 0.5–0.3907 = 0.1093
Составим расчетную таблицу для
вычисления значения χ2.
|
W
|
P
|
W–P
|
(W–P)2
|
|
|
0.1375
|
0.121
|
0.0165
|
0.00027225
|
0.00225
|
|
0.2375
|
0.2347
|
0.0028
|
0.00000784
|
0.0000334
|
|
0.3
|
0.3107
|
–0.0107
|
0.00011449
|
0.0003685
|
|
0.175
|
0.2243
|
–0.0493
|
0.00243049
|
0.010836
|
|
0.15
|
0.1093
|
0.0407
|
0.00165649
|
0.0015155
|
χ2набл. = 400∙0.015 = 6
χ2теор (0.01;4) = 13.2767
Т.к. χ2набл < χ2теор
, то гипотеза о принятом теоретическом распределении не противоречит опытным
данным.
Задача 5.
Предполагая, что диаметр валика является нормально
распределенной случайной величиной, найти по условию задачи № 4: а) выражения
для плотности и функции распределения диаметра валика; б) вероятность того, что
диаметр наугад взятого валика будет превышать 30 мк.
Решение.
а) Функция плотности f(x)
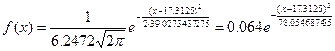
Функция распределения F(X)
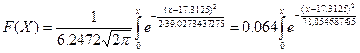
б) P(X>30)=0.5–
= 0.5– Ф(2.03) = 0.5–0.4788 = 0.0212 = 2.12%