ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 1. ВАРИАНТ 20.

1.  В 2001 г. в Ваш день рождения (7 ноября) в Сбербанке был открыт счет до востребования на сумму 6500 рублей. Ставка - 2% годовых, по условиям договора вклада начисление и капитализация процентов осуществляются по истечении каждого календарного квартала. Сколько денег получит клиент банка при закрытии счета в этот же день в 2002 г.?

Решение.

Сумма после начисления процентов в конце четвертого квартала 2001 года:

6500·(1+0.02·54/365)=6519.23 руб.

После 1 квартала 2002 года.

6519.23·(1+0.02·90/365)=6551.38 руб.

После 2 квартала.

6551.38·(1+0.02·91/365)=6584.05 руб.

После 3 квартала

6584.05·(1+0.02·92/365)=6617.24 руб.

При закрытии счета

6617.24·(1+0.02·38/365)=6631.02 руб.

2.   Какой была бы эта сумма, если бы а) начисление процентов и их капитализация осуществлялись   лишь    по   истечении    календарного   года;   б)   начисление   процентов   и    их капитализация  осуществлялись  бы  ежедневно;  в)  начисление  процентов  и  их капитализация осуществлялись бы непрерывно?

Решение.

а) Начисление процентов в конце года.

6500·(1+0.02·326/365)=6616.11 руб.

При закрытии счета

6616.11·(1+0.02·38/365)=6629.89 руб.

б) Ежедневное начисление процентов

6500·(1+0.02/365)³⁶⁵=6631.31 руб.

в) Непрерывное начисление процентов.

6500·e^0.02=6631.31 руб.

3.  Какую сумму (в условиях задачи 1) необходимо снять с этого счета ровно через 250 дней после его открытия, чтобы при закрытии счета вкладчик получил 6000 рублей?

Решение.

Снятие суммы произошло через 250 дней после открытия вклада, т.е. 16 июля 2002 года. Обозначим снятую сумму X. Получим следующее соотношение:

Сумма после начисления процентов в конце четвертого квартала 2001 года:

6500·(1+0.02·54/365)=6519.23 руб.

После 1 квартала 2002 года.

6519.23·(1+0.02·90/365)=6551.38 руб.

После 2 квартала.

6551.38·(1+0.02·91/365)=6584.05 руб.

Рассчитаем проценты за третий квартал 2002 года.

6584.05·0.02·15/365+(6584.05–X)·0.02·77/365 = 6584.05·0.02·92/365–X·0.02·77/365 = 33.19–0.00422X

Сумма после третьего квартала.

6584.05–X+33.19–0.00422X=6617.24–1.00422X

При закрытии счета

(6617.24–1.00422X)·(1+0.02·38/365) = (6617.24–1.00422X)∙1.002083 = 6631.02–1.0063118X

Так, как сумма, полученная при закрытии счета составляет 6000 рублей, получаем соотношение:

6631.02–1.0063118X=6000

1.0063118X=631.02

X=627.06 руб.

Это и будет искомая сумма.

4.  Дайте ответ на вопрос, поставленный в задаче 1, если на такую же сумму в тот же день был открыт срочный вклад на 180 дней с автоматическим продлением условий вклада на новый срок в случае неявки клиента. Ставка — 18% годовых.

Решение.

6500·(1+0.18·180/365)²∙(1+0.02·4/365)=7786.88 руб.

5.  Рассчитайте годовую эффективную ставку процента для срочного вклада на 90 дней под 17% годовых.

Решение.

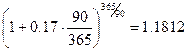
Следовательно, искомая ставка равна 18.12%.

6.   При каких расчетных ставках процента по срочным вкладам на  1  месяц годовая эффективная ставка будет превышать расчетную более чем в 1,5 раза?

Решение.

Обозначим искомую ставку x. Получим соотношение.

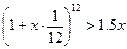
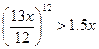
Прологарифмируем обе части неравенства.

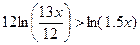
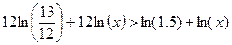
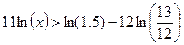
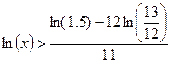
ln(x)>–0.05046

x>0.95

Следовательно, условие задачи будет выполнятся при расчетной ставке 95% годовых.

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №2. ВАРИАНТ 20.

1.  Годовая эффективная ставка процента по срочным рублевым вкладам - 14%. Ожидаемый рост курса доллара в течение ближайших 12 месяцев - 9%. Определите, при каких относительных различиях между ценами покупки и продажи в обменных пунктах имеющему доллары и нуждающе­муся через год в долларах целесообразно: а) продолжать хранить их в наличной форме; б) поменять на рубли, открыть срочный вклад и через год поменять возросшую рублевую сумму на доллары.

Решение.

Пусть n>1 – отношение курса продажи к курсу покупки, k₁ – курс доллара при покупке в начале срока. Тогда курс доллара при продаже в конце срока (через год) будет равен k₁∙n∙1.09.

S – Исходная сумма в долларах. Продав их, мы получим S∙k₁ рублей. Положив их на срочный вклад, в конце года получим S∙k₁∙1.14 рублей. Поменяв рубли на доллары мы получим (S∙k₁∙1.14)/(k₁∙n∙1.09)=(S∙1.14)/( n∙1.09) =S∙1.04587/n долларов.

Искомое относительное различие можно найти из соотношения:

S∙1.04587/n>S

1.04587/n>1

n<1.04587

То есть, если курс продажи менее чем в 1.04587 превосходит курс покупки, то более выгоден вариант б)

2. Пусть сегодня в обменных пунктах российских банков цена покупки и доллара, и евро на 5 процентных пунктов меньше цены продажи. Такой же эта разница сохранится и в будущем.  Ожида­ется с большой вероятностью, что ежемесячно в течение длительного времени курс евро по отноше­нию к доллару будет возрастать на 0.25%. Цены покупки и продажи обеих валют будут изменяться такими же темпами, как и биржевые курсы. Определите, целесообразно ли имеющему доллары и ну­ждающемуся в перспективе в долларах обменять их на евро, а затем осуществить обратный обмен, и если целесообразно, то в каком случае.

Решение.

Рассмотрим ситуацию, когда человек обменял доллары на рубли, а потом рубли на евро, а по истечении n месяцев поменял их обратно.

Начальную сумму обозначим S. Обозначим курс покупки доллара в начале операции k_d, а курс покупки евро – k_e. Продав доллары, человек получил S∙k_d рублей. Купив евро, человек получил (S∙k_d)/(k_e∙1.05) евро. Обозначим эту сумму S₁.

Прошло N месяцев. Новые курсы покупки доллара и евро соответственно обозначим l_d и l_e. Продав евро человек получил S₁∙l_e рублей. Купив доллары, человек получил (S₁∙l_e)/(l_d∙1.05) долларов. Обозначив эту сумму через S₂ и выразив ее через S получим соотношение:

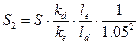
По условию задачи соотношение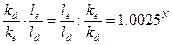

В результате получаем следующее соотношение:

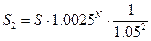
Вся эта операция выгодна при условии, что S₂>S, т.е.

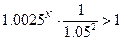
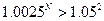
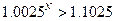
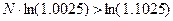
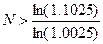
N>39.081

Т.е. целесообразно делать эту операцию на срок 40 месяцев и более.

3.  Годовая эффективная ставка процента по срочным вкладам на год во всех банках составля­ет 15%. Пусть вероятность банкротства любого банка в течение ближайшего года составляет 8%. Банкротство банка означает потерю всех вложенных в него денег. Определите математическое ожи­дание получаемой через год суммы, вероятности получить максимум и потерять все в случае, если: а) все 900000 руб. вложены в один банк; б) если деньги поровну распределены между двумя банками; в) если деньги поровну распределены между тремя банками. Задачу решить в предположении, что бан­кротство одних банков никак не сказывается на положении других, а в банковской системе страны всего 5 банков.

Решение.

а) Возможны 2 исхода (банк разорился, банк не разорился).

Вероятность первого исхода – 8%. Получаемая в этом случае сумма = 0.

Вероятность второго исхода – 92%. Получаемая в этом случае сумма = 900000·1.15 = 1035000 руб.

Математическое ожидание получаемой суммы = 1035000·0.92 = 952200 руб.

Вероятность получить максимум (1035000 руб.) – 92%.

Вероятность не получить ничего – 8%.

б) Возможны 3 исхода (ни один из банков не разорился, разорился 1 из банков, разорились оба банка). Найдем вероятность каждого исхода и полученную в каждом случае сумму.

Вероятность того, что ни один из банков не разорился, равна 0.92²=0.8464=84.64%. Полученная при этом сумма = 900000·1.15 = 1035000 руб.

Вероятность того, что разорился один из банков равна 2·0.92·0.08 = 0.1472 = 14.72%. Полученная при этом сумма 450000·1.15 = 517500 руб.

Вероятность того, что оба банка разорились равна 0.08·0.08=0.0064 = 0.64%. Полученная при этом сумма = 0.

Математическое ожидание получаемой суммы = 1035000·0.8464 + 517500·0.1472 = 952200 руб.

Вероятность получить максимум (1035000 руб.) = 84.64%

Вероятность не получить ничего = 0.64%

в) Возможны 4 исхода: разорилось 0,1,2,3 банка. Найдем вероятность каждого исхода и полученную в каждом случае сумму.

Вероятность  того, что ни один банк не разорился, равна 0.92³= 0.778688=77.8688%. Полученная при этом сумма = 900000·1.15 = 1035000 руб.

Вероятность того, что разорился 1 банк, равна 3·0.92·0.92·0.08 = 0.203136 = 20.3136%. Полученная при этом сумма = 600000·1.15 = 690000 руб.

Вероятность того, что разорились 2 банка, равна 3·0.92·0.08·0.08 = 0.017664 = 1.7664%. Полученная при этом сумма = 300000·1.15 = 345000 руб.

Вероятность того, что все три банка разорились равна 0.08·0.08·0.08=0.000512 = 0.0512%. Полученная при этом сумма = 0.

Математическое ожидание получаемой суммы = 1035000·0.778688 + 690000·0.203136 + 345000·0.017667  = 952200 руб.

Вероятность получить максимум (1035000 руб.) = 77.8688%

Вероятность не получить ничего = 0.0512%

4.  Решите задачу 3 для ситуации, когда банкротство какого-либо банка приводит к увеличе­нию вероятности банкротства всех остальных в 2 раза.

Решение.

а) Возможны 2 исхода (банк разорился, банк не разорился).

Вероятность первого исхода – 8%. Получаемая в этом случае сумма = 0.

Вероятность второго исхода – 92%. Получаемая в этом случае сумма = 900000·1.15 = 1035000 руб.

Математическое ожидание получаемой суммы = 1035000·0.92 = 952200 руб.

Вероятность получить максимум (1035000 руб.) – 92%.

Вероятность не получить ничего – 8%.

б) Возможны 3 исхода (ни один из банков не разорился, разорился 1 из банков, разорились оба банка). Найдем вероятность каждого исхода и полученную в каждом случае сумму.

Вероятность того, что ни один из банков не разорился, равна 0.92=92%. Полученная при этом сумма = 900000·1.15 = 1035000 руб.

Вероятность того, что разорился один из банков равна 0.08·0.84 = 0.0672 = 6.72%. Полученная при этом сумма 450000·1.15 = 517500 руб.

Вероятность того, что оба банка разорились равна 0.08·0.16=0.0128 = 1.28%. Полученная при этом сумма = 0.

Математическое ожидание получаемой суммы = 1035000·0.92 + 517500·0.0672 = 986976 руб.

Вероятность получить максимум (1035000 руб.) = 92%

Вероятность не получить ничего = 1.28%

в) Возможны 4 исхода: разорилось 0,1,2,3 банка. Найдем вероятность каждого исхода и полученную в каждом случае сумму.

Вероятность  того, что ни один банк не разорился, равна 0.92= 92%. Полученная при этом сумма = 900000·1.15 = 1035000 руб.

Вероятность того, что разорился 1 банк, равна 0.08·0.84 = 0.0672 = 6.72%. Полученная при этом сумма = 600000·1.15 = 690000 руб.

Вероятность того, что разорились 2 банка, равна 0.08·0.16·0.68 = 0.008704 = 0.8704%. Полученная при этом сумма = 300000·1.15 = 345000 руб.

Вероятность того, что все три банка разорились равна 0.08·0.16·0.32=0.004096 = 0.4096%. Полученная при этом сумма = 0.

Математическое ожидание получаемой суммы = 1035000·0.92 + 690000·0.0672 + 345000·0.008704  = 1001570.88 руб.

Вероятность получить максимум (1035000 руб.) = 92%

Вероятность не получить ничего = 0.4096%

5.  Ставка процента по срочным вкладам на месяц составляет 1,2%. за период и таковой она сохранится в перспективе. Ежемесячный рост цен на жилье составляет 1.4%. Определите, для каких временных периодов вложение в жилье с целью последующей перепродажи будет более выгодной финансовой операцией, чем хранение денег в банке, если издержки на покупку жилья составляют 7% от его рыночной цены, издержек при продаже нет. Задачу решить без учета возможности сдачи в аренду и необходимости платить за жилье.

Решение.

Обозначим начальную сумму S. Количество прошедших месяцев – N.

Если хранить деньги в банке, то в конце периода получим сумму S∙1.012^N.

Если купить жилье, а через N месяцев его продать, то получим сумму S∙0.93∙1.014^N.

Покупка и последующая продажа жилья будет выгодна при выполнении следующего условия:

S∙0.93∙1.014^N> S∙1.012^N

0.93∙1.014^N> 1.012^N

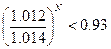
0.998^N<0.93

N∙ln0.998<ln0.93

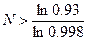
N>36.25

Получается, что покупка и последующая продажа жилья более выгодна, чем хранение денег в банке при сроке более 37 месяцев.

6.  В ювелирном отделе какого-нибудь магазина узнайте, по какой цене продается 1 г золота в простых золотых изделиях (типа обручальных колец). Не забудьте посмотреть на пробу. Рассчитайте, во сколько раз в этих изделиях золото дороже, чем на мировых товарных биржах.

Решение.

Цена золота в магазине.

Исходные данные: Обручальное кольцо весом 1.95 грамма из золота 585 пробы стоит в магазине 965 рублей.

Цена одного грамма золота равна:

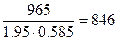рублей.

Цена золота на мировых биржах составляет 317 долларов за тройскую унцию (31.1 грамма).

Курс доллара – 29.25 рублей за доллар.

317 долларов = 317∙29.25=9272.25

Цена одного грамма – 9272.25/31.1=298.14 руб.

Получаем, что в магазине золото в 846/298.14 = 2.8376 раз дороже.

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №3. ВАРИАНТ 20.

1.  Кредит на сумму 8 млн. руб. получен на условиях погашения его единовременным пла­тежом вместе с процентами через 5 месяцев. Какую сумму должен будет возвратить заемщик кре­дитору, если:   а) кредиты на такие сроки предоставляются исходя из расчетной ставки 16% годо­вых, а для исчисления стоимости кредита используется формула простых процентов: б) для креди­тов на любые сроки используется годовая эффективная ставка - 16%?

Решение.

а) 8000000·(1+0.16·5/12)=8533333.33 рублей.

б) 8000000·(1+0.16)^5/12=8510351.2 рублей.

2.  Какие суммы должен ежемесячно отдавать заемщик кредитору, если бы погашение кре­дита предусматривалось пятью равными суммами — соответственно через 1 месяц, 2, 3. 4 и 5 меся­цев, если: а) расчетная ставка остается такой же, как в задаче 1. и для соизмерения денежных сумм во времени используется формула простых процентов: б) годовая эффективная ставка остается такой же, как в задаче 1, и для соизмерения денежных сумм во времени используется формула сложных процентов?

Решение.

а) Обозначим искомую сумму x.

Получим соотношение.

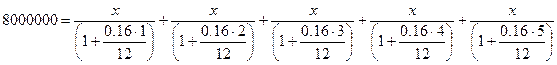
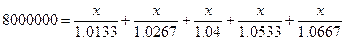
8000000 = 0.9869x+0.974x+0.9615x+0.9494x+0.9375x

8000000 = 4.8093x

x=1663443.74

б) Обозначим искомую сумму x.

Получим соотношение.

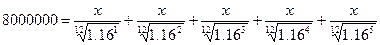
По формуле суммы геометрической прогрессии получим:

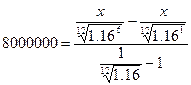
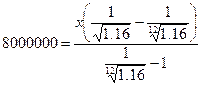
8000000 = 4.8186x

x=1660233.26

3. Какие суммы в условиях задачи 1 получил бы на руки заемщик, если бы кредитор взял с него проценты в момент выдачи кредита?

Решение.

8000000/(1+0.16·5/12)=7500000 руб.

4.  Какими были бы уплачиваемые единовременно по окончании срока займа проценты за кредит, если в условиях задачи 2 в указанные сроки равными долями погашался основной долг?

Решение.

8000000·0.16/12+6400000·0.16/12+4800000·0.16/12+3200000·0.16/12+1600000·0.16/12 = 24000000·0.16/12 = 320000 руб.

5.  Согласованный с кредитором график погашения кредита предполагал ежемесячную вы­плату заемщиком 1 млн. руб. в течение 12 месяцев (1-й платеж - через месяц после получения кре­дита, 2-й - через 2 месяца и т.д.). После совершения 6 платежей заемщик попросил кредитора раз­решить погасить ему весь остаток долга единовременно по завершении срока кредита. Сколько он должен будет заплатить кредитору по истечении 12-го месяца при условии, его фактические пла­тежи будут финансово эквивалентными прежнему графику погашения долга, если для соизмере­ния денежных сумм во времени используется годовая эффективная ставка 24%.

Решение.

Обозначим искомую сумму S. Получим соотношение.

1000000∙6.308120963 = S∙1.1040808

S=5713459.52 руб.

6.  Кредиты на 4 месяца выдаются исходя из расчетной ставки 25% годовых. Исходя из ка­кой расчетной ставки должны выдаваться кредиты на 10 месяцев, чтобы годовая эффективная ставка процента по таким кредитам была такой же, как и по кредитам на 4 месяца?

Решение.

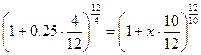
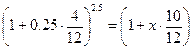
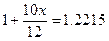
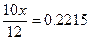
x=0.2658

Получаем расчетную ставку 26.58%

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 4. ВАРИАНТ 20.

1.   Облигации   внутреннего   выигрышного   займа   выпущены   на   следующих условиях. Всего облигаций 10 млн. штук, срок погашения - через 6 лет. Ежегодно в конце каждого календарного квартала проводится тираж, в результате которого 200000 облигаций выигрывают. Выигравшие облигации в дальнейших тиражах не участвуют. Определите  вероятность  выигрыша  в   10-м  тираже для  человека,   имеющего три облигации.

Решение.

Всего облигаций 10000000 штук. После 9 тиражей 1800000 из них выбудут из розыгрыша. Останется 10000000–1800000=8200000 облигаций. Вероятность выигрыша в 10 тираже для человека, имеющего 3 облигации равна 3/8200000.

2. На фондовом рынке обращаются дисконтные облигации номиналом в 100 тыс. руб. Какова будет их рыночная цена за 3 месяца до погашения, если вложения в эти облигации обеспечивают такую же доходность, как и обычные кредитные операции, годовая эффективная ставка для которых составляет 24%?

Решение.

Рассчитаем доходность кредита на 3 месяца при 24% годовых.

0.24∙3/12=0.06=6%

Дисконт равен

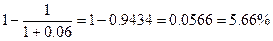
Следовательно рыночная цена акций за 3 месяца до погашения будет равна

100000∙(1–0.0566) = 943400 рублей.

3.  Банк учитывает векселя, срок оплаты которых - через 100 дней, с дисконтом 4,8%. Какова доходность таких операций в пересчете на годовую эффективную ставку декурсивных процентов?

Решение.

Обозначим доходность операции x. Получим следующее соотношение:

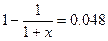
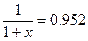
1+x=1.05042

x=0.05042

Годовая эффективная ставка.

0.05042∙365/100=0.184=18.4%

4. Рассчитайте формальную рыночную стоимость акций, по которым ежегодно выплачивается дивиденды в размере 150 руб. на одну акцию, если до момента получения первых дивидендов остается 10 месяцев. Годовая эффективная ставка процента составляет 12%.

Решение.

Стоимость акции сразу после выплаты дивидендов = 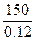= 1250 рублей.

В день выплаты дивидендов стоимость акции будет равна 1250+150=1400 рублей.

Стоимость акции на момент, когда до выдачи дивидендов остается 10 месяцев равна

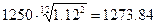руб.

5.  Стартовая формальная рыночная цена купонной облигации (всего 4 купона) номиналом 500 тыс. руб., погашаемой через 2 года, по которой по истечении каждых шести месяцев выплачивается доход в размере 5% от номинала, составляет 450 тыс. руб. Определите годовую эффективную ставку процента на денежном рынке.

Решение.

Обозначим искомую ставку x. Получим следующее соотношение.

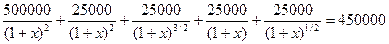
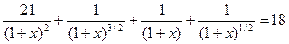
Подбором найдем x=0.1668=16.68%

6.  Рассчитайте современную стоимость отложенной обыкновенной ежегодной ренты  в 50000 руб.   на 5  лет,   в  предположении,  что годовая эффективная ставка процента на денежном рынке составляет и будет составлять 12%, а первые 50000 руб. можно получить через 4 года.

Решение.

Искомая цена

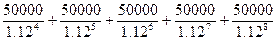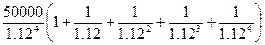 =  = 128290.42 руб.

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №5. ВАРИАНТ 20.

1. Номинальная годовая эффективная ставка процента на денежном рынке составляет 28%. Чему равна реальная ставка процента, если рост среднего уровня цен за год составляет: а) 15% ; б) 26%; в) 56%?

Решение.

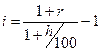, где i – реальная ставка процента, r – номинальная ставка, h – рост среднего уровня цен.

а)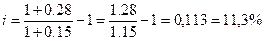

б)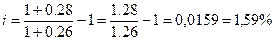

в)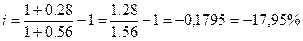

2 Фирма осуществляет розничную торговлю товаром по цене 200 руб. за штуку. Ежедневный объем продаж - 200 единиц. Закупка товара осуществляется только на заемные средства, которые берутся под 0,1% в день (проценты простые). Закупка товара осуществляется на оптовой базе, оптовая цена не зависит от объема партии и равна 150 руб. за 1 шт. Однако с каждого клиента при совершении сделки база берет дополнительно 3000 руб.

Количество закупаемых единиц товара должно быть кратно 200. Определите оптимальную стратегию закупок товара фирмой, т.е. такую, при которой среднесуточный чистый доход фирмы будет максимальным, если: а) кредит вместе с процентами возвращается единовременно после распродажи очередной партии товара; б) основной долг погашается равными долями в течение всего срока распродажи партии товара и ежедневно выплачиваются проценты за пользование в течение суток оставшейся суммой основного долга; в) кредит вместе с процентами возвращается единовременно, но до распродажи всей партии товара, в максимально короткий срок. В последнем случае достаточно найти дробное решение.

Решение.

Обозначим через 200∙n – количество закупаемых единиц товара. Найдем прибыль фирмы от реализации данной партии товара.

а) Затраты на покупку товара – 150∙200∙n+3000=30000n+3000 рублей.

Это будет размер кредита.

Размер начисленных процентов за n дней.

(30000n+3000)∙0.001∙n = (30n+3)∙n = 30n²+3n

Полученный доход 200∙200∙n=40000n рублей.

Размер полученной прибыли равен

40000n–30000n–3000–30n²–3n = –30n²+9997n–3000

Среднесуточный чистый доход фирмы равен

–30n+9997–3000/n

Найдем максимум полученной функции от n.

Производная

–30+3000/n²=0

3000/n²=30

n²=100

n=10

Соответственно, оптимальный размер партии будет 200∙10=2000 единиц товара.

б) Затраты на покупку товара – 150∙200∙n+3000=30000n+3000 рублей.

Это будет размер кредита.

Каждый день выплачивается 30000+3000/n рублей для погашения долга.

Проценты за i-й день будут начислены в сумме.

(30000+3000/n)∙0.001∙(n–i+1)

Сумма процентов будет равна 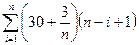 =  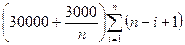=  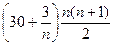= (15n+1.5)(n+1) = 15n²+16.5n+1.5

Размер полученной прибыли равен

40000n–30000n–3000–15n²–16.5n–1.5 = 9983.5n–15n²–3001.5

Среднесуточный чистый доход фирмы равен

–15n+9983.5–3001.5/n

Найдем максимум полученной функции от n.

Производная

–15+3001.5/n²

n²=200.1

n=14.146

Найдем значение среднесуточного дохода для граничных целых значений.

n=14.

Среднесуточный чистый доход фирмы равен

–15∙14+9983.5–3001.5/14 = –210+9983.5–214.39 = 9559.11 руб.

n=15.

Среднесуточный чистый доход фирмы равен

–15∙15+9983.5–3001.5/15 = –225+9983.5–200.1 = 9558.4 руб.

Соответственно, оптимальный размер партии будет 200∙14=2800 единиц товара.

в) Затраты на покупку товара – 150∙200∙n+3000=30000n+3000 рублей.

Это будет размер кредита.

Для того, чтобы накопить сумму 30000n рублей необходимо торговать 3n/4 дня. Для того чтобы покрыть 3000 руб. за совершение сделки и проценты надо затратить еще один день.

За это время накопятся проценты

(30000n+3000)∙0.001∙(3n/4+1) = (30n+3)∙(3n/4+1) = ((90/4)n²+(30+9/4)n+3) руб.

Размер полученной прибыли равен

40000n–30000n–3000–(90/4)n²–(129/4)n–3 = –(129/4)n²+(10000–129/4)n–3003

Среднесуточный чистый доход фирмы равен

–(129/4)n+(10000–129/4)–3003/n

Найдем максимум полученной функции от n.

Производная

–(129/4)+3003/n²=0

n²=3003∙4/129 = 93.116

n=9.65

3.  Ежедневное потребление чая в семье составляет 10 грамм. Его продают в магазине на вес по цене 100 руб. за 1 кг, фасуя в безразмерные фирменные пакеты стоимостью 1 руб. Если ежедневно покупать по 10 г, то придется платить 2 руб., если раз в n дней покупать по 10n г. то платить придется по (n+1) рублей. Определите с позиций   формальной финансовой математики оптимальный режим покупок, если годовая эффективная станка процента по депозитам составляет 8%.

Решение.

Обозначим n – то количество дней, на которое оптимально покупать чай.

Затраты на покупку чая составят 10(n+1) рублей.

Реальные траты за эти n дней составят 10(n+1)∙1.08^n/365

Реальные траты за 1 день составят 10(1+1/n)∙1.08^n/365

Найдем минимум полученной функции от n.

Производная

10((–1/n²)∙1.08^n/365+(1+1/n)∙(1/365)∙ln(1.08)∙1.08^n/365 = 10∙1.08^n/365((–1/n²) + (1+1/n)∙(1/365)∙ln(1.08)) = –10∙1.08^n/365(1/n² – 0.00021/n – 0.00021)

Обозначим x=1/n. Получим соотношение.

x²–0.00021x–0.00021=0

D=0.00021²+0.00084 = 0.0008400441

x=(0.00021±0.02898)/2

Отрицательное x не подходит по смыслу задачи.

x=0.014595

n=1/0.014595 = 68.5166

Получается, что оптимально покупать чай на 69 дней.

4.   Семья арендует квартиру  и  платит за нее ежемесячно 3500  руб.  Текущие доходы позволяют ежемесячно откладывать  4000  руб.   (остальное  уходит на  неотложные  нужды   и хозяину). Есть мечта приобрести собственную квартиру стоимостью 500000 руб. Предположив, что деньги  накапливаются  в  наличной  форме,  определите,  стоит ли для ускорения  решения проблемы прибегнуть к банковскому кредиту, который на любые сроки выдается под годовую эффективную  ставку 8%. И  если  целесообразно,   то  когда  (после  накопления   какой  суммы собственных средств) это лучше всего сделать?

Решение.

Обозначим t – количество месяцев, в течении которых семья накапливает деньги. После этого они берут кредит, в размере (500000–4000t) рублей. Обозначим n – число месяцев в течении которых они погасят кредит. Получаем соотношение:

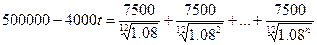
В правой части равенства стоит геометрическая прогрессия.

Найдем ее сумму по формуле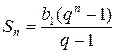

 =  =  =  =  =

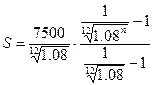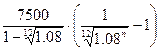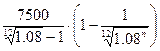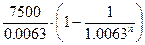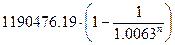В итоге получаем соотношение:

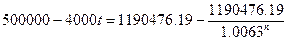
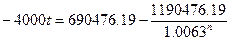
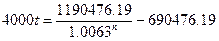
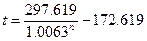
Нам надо найти решение, при котором t+n→min.

Выразив t через n получим задачу нахождения наименьшего значения функции одной переменной.

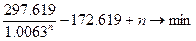
Найдем производную данной функции.

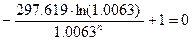
1.0063ⁿ = 297.619∙ln(1.0063)

1.0063ⁿ = 1.869

n∙ln(1.0063) = ln(1.869)

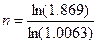
n=99.583

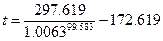 = –13.38

Так как получилось отрицательное число, то оптимальной стратегией будет сразу взять кредит.

5.  Определите с позиций формальной финансовой математики: какой автомобиль лучше – ценой 60000 руб., сроком службы 6 лет. с ежегодными издержками на эксплуатацию 14000 руб. или ценой 100000 руб., сроком службы 10 лет, с ежегодными издержками на эксплуатацию 13000 руб. Годовая эффективная ставка составляет 6%.

Решение.

Рассчитаем реальные расходы в год в том и другом случае.

Расходы по первому автомобилю:

Покупка – 60000 руб.

Издержки на эксплуатацию:

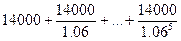 = 72793.09

Итого получаем расходы в год:

(60000+72793.09)/6 = 22132.18 руб.

По второму автомобилю:

Покупка – 100000 руб.

Издержки на эксплуатацию:

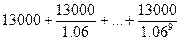 = 101422

Итого получаем расходы в год:

(100000+101422)/10 = 20142.2 руб.

Получаем, что второй автомобиль лучше.

6.  Ежедневный объем продаж торговой фирмы - 500 кг, розничная цена 1 кг - 40 рублей. Единовременные затраты на доставку партии товара с базы - 2000 рублей. Оптовая цена 1 кг - 30 рублей. Затраты на хранение 1 кг товара (имеющегося в наличии ни начало рабочего дня) составляют 50 копеек. Требуется определить оптимальный размер закупаемой партии товара, обеспечивающий после ее распродажи максимум дохода фирмы в расчете на 1 день торговли.

Решение.

Обозначим оптимальный размер партии 500∙n.

Найдем расходы.

Закуп по оптовой цене.

30∙500∙n = 15000n рублей.

Доставка товара – 2000 рублей.

Затраты на хранение после i-го дня.

0.5∙500∙(n–i)

Общие затраты на хранение.

0.5∙500∙(n–1)∙n/2 = 125n(n–1) = 125n²–125n

Доходы от продажи товара.

40∙500∙n = 20000n рублей.

Общий доход.

20000n–15000n–2000–125n²+125n=5125n–2000–125n²

Среднесуточный чистый доход фирмы равен

–125n+5125–2000/n

Найдем максимум полученной функции от n.

Производная

–125+2000/n²=0

n²=16

n=4.

Следовательно, оптимальный объем закупок составит 500∙4=2000 кг.