Содержание
Исходные
данные. 3
1.
Проверка на нормальность. 3
2.
Избавиться от выбросов. 5
3.
Проверить гипотезу равенства средних. 6
4.
Достоверность отличия каждого из средних от нуля. 7
5.
Гипотетическая разность между средними. 7
6.
Минимальное количество объектов. 8
Исходные данные
Дано два массива данных:
Х: 5 6 7 5,5 5,8
Y: 22 21 21,5 20 80
1. Проверка на нормальность
По Критерию Пирсона проверим две статистические гипотезы о
том, что каждая из выборок имеет нормальное распределение. Сначала составим в
пакете Excel вспомогательную
таблицу:
|
Х
|
Y
|
Х*Х
|
Y*Y
|
|
5
|
22
|
25
|
484
|
|
6
|
21
|
36
|
441
|
|
7
|
21.5
|
49
|
462.25
|
|
5.5
|
20
|
30.25
|
400
|
|
5.8
|
80
|
33.64
|
6400
|
|
Сумма
|
29.3
|
164.5
|
173.89
|
8187.25
|
|
Среднее
|
5.86
|
32.9
|
34.778
|
1637.45
|
Используя данные этой таблицы найдем среднеквадратичные
отклонения каждой из выборок:
Приведем формулы, по которым проводились эти вычисления в Excel:
|
Х
|
Y
|
Х*Х
|
Y*Y
|
|
5
|
22
|
=B2*B2
|
=C2*C2
|
|
6
|
21
|
=B3*B3
|
=C3*C3
|
|
7
|
21.5
|
=B4*B4
|
=C4*C4
|
|
5.5
|
20
|
=B5*B5
|
=C5*C5
|
|
5.8
|
80
|
=B6*B6
|
=C6*C6
|
|
Сумма
|
=СУММ(B2:B6)
|
=СУММ(C2:C6)
|
=СУММ(D2:D6)
|
=СУММ(E2:E6)
|
|
Среднее
|
=B7/5
|
=C7/5
|
=D7/5
|
=E7/5
|
|
|
|
|
|
|
СКО
Х
|
=КОРЕНЬ((5/4)*(D8-B8*B8))
|
|
|
|
|
СКО
Y
|
=КОРЕНЬ((5/4)*(E8-C8*C8))
|
|
|
|
Далее проведем основные вычисления по проверке гипотез. Для
этого сгруппируем значения из этих выборок по интервалам. Для первой выборки этими
интервалами будут (–¥;5),
[5;6), [6;7), [7;8), [8;+¥).
Для второй выборки этими интервалами будут (–¥;20), [20;21], (21;22], (22;80], (80;+¥).
Ниже приведены таблицы их Excel, в которых как для первой, так и для второй выборок
приведены эмпирические частоты попадания элементов выборок в каждый интервал, центрированные
и нормированные значения границ интервалов, значения стандартной функции
Лапласа в центрированных и нормированных границах интервалов, значения функций
нормального распределения в границах интервалов (для вычисления теоретических
вероятностей попадания элементов выборки в указанные интервалы), теоретические
частоты попадания элементов выборки в указанные интервалы, значения c2-критериев
для каждой выборки.
|
Х
|
m(i)
эмп
|
Z
|
Ф(Z)
|
F(x(I))
|
F(x(i+1))
|
m(i)
теор
|
Хи-кв
|
|
|
0
|
|
-0.5
|
0
|
0.623
|
0
|
0
|
|
5
|
3
|
-1.162
|
0.123
|
0.623
|
0.813
|
0.954
|
4.392
|
|
6
|
1
|
0.189
|
0.575
|
1.075
|
1.438
|
1.816
|
0.367
|
|
7
|
1
|
1.540
|
0.938
|
1.438
|
1
|
-2.191
|
-4.647
|
|
|
0
|
|
0.5
|
1
|
|
0
|
0
|
|
Сумма
|
5
|
|
|
|
|
Сумма
|
0.11151
|
|
|
|
|
|
|
|
|
|
Y
|
m(i)
эмп
|
Z
|
Ф(Z)
|
F(y(I))
|
F(y(i+1))
|
m(i)
теор
|
Хи-кв
|
|
|
0
|
|
-0.5
|
0
|
0.623
|
0
|
0
|
|
20
|
3
|
-0.490
|
0.312
|
0.812
|
0.813
|
0.006
|
1471.928
|
|
22
|
1
|
-0.414
|
0.340
|
0.840
|
1.438
|
2.994
|
1.328
|
|
80
|
1
|
1.788
|
0.963
|
1.463
|
1
|
-2.316
|
-4.747
|
|
|
0
|
|
0.5
|
1
|
|
0
|
0
|
|
Сумма
|
5
|
|
|
|
|
Сумма
|
1468.508
|
Ниже приведем ту же таблицу из Excel? Только с указанием формул:
|
Х
|
m(i) эмп
|
Z
|
Ф(Z)
|
F(x(I))
|
F(x(i+1))
|
m(i) теор
|
Хи-кв
|
|
|
0
|
|
-0.5
|
=0.5+D14
|
0.62267
|
0
|
0
|
|
5
|
3
|
=(A15-B$8)/B$10
|
=НОРМРАСП(C15;0;1)
|
=0.5+D15
|
0.81337
|
=(F15-E15)*B$19
|
=СТЕПЕНЬ(B15-G15;2)/G15
|
|
6
|
1
|
=(A16-B$8)/B$10
|
=НОРМРАСП(C16;0;1)
|
=0.5+D16
|
1.43821
|
=(F16-E16)*B$19
|
=СТЕПЕНЬ(B16-G16;2)/G16
|
|
7
|
1
|
=(A17-B$8)/B$10
|
=НОРМРАСП(C17;0;1)
|
=0.5+D17
|
1
|
=(F17-E17)*B$19
|
=СТЕПЕНЬ(B17-G17;2)/G17
|
|
|
0
|
|
0.5
|
=0.5+D18
|
|
0
|
0
|
|
=СУММ(B14:B18)
|
|
|
|
|
Сумма
|
=СУММ(H14:H18)
|
|
Y
|
m(i) эмп
|
Z
|
Ф(Z)
|
F(y(I))
|
F(y(i+1))
|
m(i) теор
|
Хи-кв
|
|
|
0
|
|
-0.5
|
=0.5+D22
|
0.62267
|
0
|
0
|
|
20
|
3
|
=(A23-C$8)/B$11
|
=НОРМРАСП(C23;0;1)
|
=0.5+D23
|
0.81337
|
=(F23-E23)*B$27
|
=СТЕПЕНЬ(B23-G23;2)/G23
|
|
22
|
1
|
=(A24-C$8)/B$11
|
=НОРМРАСП(C24;0;1)
|
=0.5+D24
|
1.43821
|
=(F24-E24)*B$27
|
=СТЕПЕНЬ(B24-G24;2)/G24
|
|
80
|
1
|
=(A25-C$8)/B$11
|
=НОРМРАСП(C25;0;1)
|
=0.5+D25
|
1
|
=(F25-E25)*B$27
|
=СТЕПЕНЬ(B25-G25;2)/G25
|
|
|
0
|
|
0.5
|
=0.5+D26
|
|
0
|
0
|
|
=СУММ(B22:B26)
|
|
|
|
|
Сумма
|
=СУММ(H22:H26)
|
Итак, расчетные значения c2-критериев для
обеих выборок 0,37311 и 163,551. Судя по таблице критических значений критерия
Пирсона при п=5 элементах выборки и
при k=2 степенях свободы, мы можем принять гипотезу о том, что
первая выборка сделана из нормально распределенной генеральной совокупности
только при уровне значимости a=0,9 (т.е. с 10%-ой надежностью), а для второй выборки
аналогичную гипотезу можем принять при уровне значимости a=0,01
(т.е. с 99%-ой надежностью).
2. Избавиться от выбросов
Для избавления от выбросов в каждой выборке проведем
экспоненциальное сглаживание и заменим элементы выборок на «сглаженные»
значения. Экспоненциальное сглаживание проведем, получив соответствующие
уравнения трендов на точечном (графическом) представлении выборок:
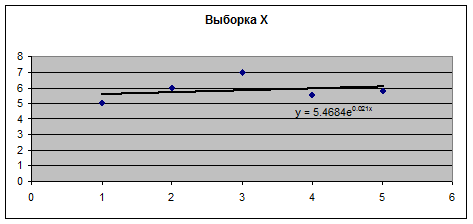
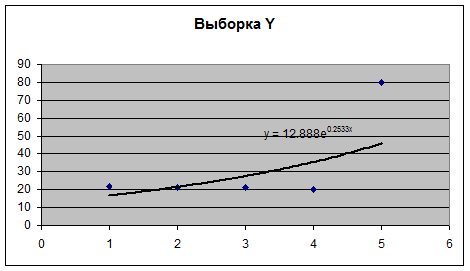
С помощью полученных уравнений вычислим «сглаженные»
значения:
|
X
|
5
|
6
|
7
|
5.5
|
5.8
|
|
Сглаж
Х
|
6.07381
|
6.2027086
|
6.3343
|
6.137921
|
6.1767119
|
|
Y
|
22
|
21
|
21.5
|
20
|
80
|
|
Сглаж
Y
|
22.5009
|
21.938139
|
22.218
|
21.38943
|
47.7777
|
3. Проверить гипотезу равенства средних
Предполагая, что обе эти выборки сделаны независимо друг от
друга из нормально распределенных генеральных совокупностей, проверим
статистичекую гипотезу о равенстве средних при условии, что гипотеза о
равенстве дисперсий не отвергается.
В качестве критерия используем функцию
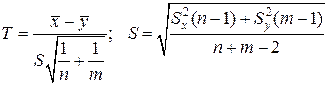 ,
,
где п=т=5
– количество элементов во обеих выборках, 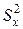 и
и 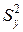 – выборочные
дисперсии.
– выборочные
дисперсии.
Вычислив в Excel эти
значения, получим следующие значения (с указанием формул):
|
S=
|
18.6326
|
=КОРЕНЬ((B10*B10*4+B11*B11*4)/8)
|
|
Т=
|
-2.2946
|
=(B8-C8)/(C39*КОРЕНЬ(1/5+1/5))
|
Функция Т подчинена
t-распределению. По таблице
t-распределения для п+т–2=8 степеней свободы и при уровне
значимости a=0,05
двусторонняя критическая область (–¥;–1,86)È(1,86;+¥),
т.е. значение Т = –2,2946 попадает в
критическую область, т.е. разность между средними несущественна и следует
принять гипотезу о равенстве средних генеральных совокупностей.
4. Достоверность отличия
каждого из средних от нуля
Для проверки достоверности
отличия каждой средней от нуля по критерию Стьюдента проверим две
статистические гипотезы о значениях средних:
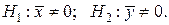
Вычислим наблюдаемые значения
критериев Стьюдента
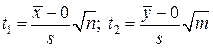 , где s – соответствующие с.к.о.:
, где s – соответствующие с.к.о.:
|
t1=
|
17.701
|
=(B8/B10)*КОРЕНЬ(5)
|
|
t2=
|
2.7930
|
=(C8/B11)*КОРЕНЬ(5)
|
Двусторонние критические области
определяем для уровня значимости a=0,05 и числе степеней свободы п–1=т–1=4
есть (–¥;–2,776)È(2,776;+¥). Это означает, что для
обеих выборок следует принимать гипотезы об отличии каждой из средних от нуля.
5. Гипотетическая разность между средними
Для гипотетической разности между
средними (d=1,2;
a=5%;
b=10%;
D=0,5) определить
минимальное количество экспериментов, необходимое для достоверного определения
гипотетической разности между средними.
Минимальное число экспериментов
найдем из следующих условий.
1) Стандартная ошибка разности
между средними находится по формуле 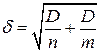 , где п и т – искомые минимальные значения
экспериментов.
, где п и т – искомые минимальные значения
экспериментов.
2) Наблюдаемое
значение t-критерия Стьюдента, используемое
при проверке статистической гипотезы о значении разности между средними
вычисляется по формуле 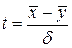 с уровнями значимости a=5% и
b=10%
и числом степеней свободы N=(n-1)+ (m-1).
с уровнями значимости a=5% и
b=10%
и числом степеней свободы N=(n-1)+ (m-1).
Используем
эти два условия для составления двух уравнений относительно двух неизвестных п и т.
Первое
уравнение 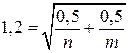 .
.
Для второго
уравнения найдем в Excel с указанием формулы
|
Дельта=
|
1.2
|
|
t=
|
22.533
|
|
Дельта=
|
1.2
|
|
t=
|
=(C8-B8)/C45
|
Для того,
чтобы гипотеза была принята с t=22,533 и a=5%,
по таблице значений критерия Стьюдента находим минимально необходимое число
степеней свободы N=1. Аналогичная картина и для
уровня значимости b=10%.
Значит,
достаточно использовать только первое уравнение для обоих случаев. Для простоты
предположим, что п=т.
Тогда искомое
минимальное число экспериментов 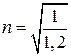 :
:
|
n=
|
0.912870929
|
=КОРЕНЬ(1/1.2)
|
Ответ:
минимальное число – 1 эксперимент.
6. Минимальное количество объектов
Для a=5% и
b=5%
определить минимальное количество объектов, которое необходимо взять в
эксперимент, для того, чтобы определить разницу между двумя ожидаемыми
частотами p1=0,2; p2=0,7.
Рассмотрим c2-критерию проверки статистической гипотезы о
совпадении ожидаемой и наблюдаемой частот. Статистика этого критерия:
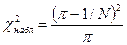 ,
,
где
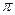 – ожидаемая частота, N – искомое минимальное
число объектов, 1/N
– наблюдаемая частота (частота появления 1 элемента с заданным свойством).
– ожидаемая частота, N – искомое минимальное
число объектов, 1/N
– наблюдаемая частота (частота появления 1 элемента с заданным свойством).
Критическое значение 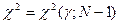 , где g – заданный уровень значимости при (N–1) степенях свободы.
, где g – заданный уровень значимости при (N–1) степенях свободы.
Гипотеза о совпадении частот принимается при выполнении
неравенства
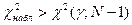 .
.
Значит, эта гипотеза отвергается
при неравенстве 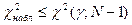 Подробнее:
Подробнее:
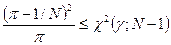 .
.
Откуда 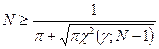 – с помощью Excel подбором
решим это неравенство относительно искомого N. Для этого поместим в Excel часть
табличных значений хи-квадрат-критерия для уровня значимости a=0,05
и для разных степеней свободы. Итак, для
– с помощью Excel подбором
решим это неравенство относительно искомого N. Для этого поместим в Excel часть
табличных значений хи-квадрат-критерия для уровня значимости a=0,05
и для разных степеней свободы. Итак, для
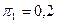 вычисления выглядят:
вычисления выглядят:
|
Пи=
|
0,2
|
|
|
|
|
|
Хи-квадр
|
N
|
Левая
часть
|
|
12,706
|
1
|
|
|
4,303
|
2
|
0,557378
|
|
3,182
|
3
|
0,886772
|
|
2,776
|
4
|
1,002258
|
|
2,571
|
5
|
1,05807
|
|
2,447
|
6
|
1,090421
|
|
2,365
|
7
|
1,111641
|
|
2,306
|
8
|
1,126443
|
|
2,262
|
9
|
1,137505
|
|
2,228
|
10
|
1,145991
|
Из этой таблицы видно что
неравенство выполняется уже при N=2.
То же самое с формулами:
|
Пи
|
0,2
|
|
|
|
|
|
Хи-квадр
|
N
|
Левая
часть неравенства
|
|
12,706
|
1
|
|
|
4,303
|
2
|
=1/(B$1+КОРЕНЬ(B$1*A4))
|
|
3,182
|
3
|
=1/(B$1+КОРЕНЬ(B$1*A5))
|
|
2,776
|
4
|
=1/(B$1+КОРЕНЬ(B$1*A6))
|
|
2,571
|
5
|
=1/(B$1+КОРЕНЬ(B$1*A7))
|
|
2,447
|
6
|
=1/(B$1+КОРЕНЬ(B$1*A8))
|
|
2,365
|
7
|
=1/(B$1+КОРЕНЬ(B$1*A9))
|
|
2,306
|
8
|
=1/(B$1+КОРЕНЬ(B$1*A10))
|
|
2,262
|
9
|
=1/(B$1+КОРЕНЬ(B$1*A11))
|
|
2,228
|
10
|
=1/(B$1+КОРЕНЬ(B$1*A12))
|
Аналогичные вычисления для 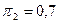 .
.
|
Пи
|
0,7
|
|
|
|
|
|
Хи-квадр
|
N
|
Левая часть
|
|
12,706
|
1
|
0
|
|
4,303
|
2
|
0,271568327
|
|
3,182
|
3
|
0,41058652
|
|
2,776
|
4
|
0,456111232
|
|
2,571
|
5
|
0,477557864
|
|
2,447
|
6
|
0,489828952
|
|
2,365
|
7
|
0,497815076
|
|
2,306
|
8
|
0,503356799
|
|
2,262
|
9
|
0,507482395
|
|
2,228
|
10
|
0,510638586
|
То же самое с формулами:
|
Пи
|
0,7
|
|
|
|
|
|
Хи-квадр
|
N
|
Левая часть неравенства
|
|
12,706
|
1
|
|
|
4,303
|
2
|
=1/(B$1+КОРЕНЬ(B$1*A4))
|
|
3,182
|
3
|
=1/(B$1+КОРЕНЬ(B$1*A5))
|
|
2,776
|
4
|
=1/(B$1+КОРЕНЬ(B$1*A6))
|
|
2,571
|
5
|
=1/(B$1+КОРЕНЬ(B$1*A7))
|
|
2,447
|
6
|
=1/(B$1+КОРЕНЬ(B$1*A8))
|
|
2,365
|
7
|
=1/(B$1+КОРЕНЬ(B$1*A9))
|
|
2,306
|
8
|
=1/(B$1+КОРЕНЬ(B$1*A10))
|
|
2,262
|
9
|
=1/(B$1+КОРЕНЬ(B$1*A11))
|
|
2,228
|
10
|
=1/(B$1+КОРЕНЬ(B$1*A12))
|
Также из этой таблицы видно, что
неравенство выполняется уже при N=2.
Ответ: для 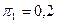 и
и 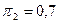 минимальное число
объектов равно 2.
минимальное число
объектов равно 2.