Содержание
Исходные
данные.. 3
1.
Описательная статистика.. 4
1)
Группировка данных. 4
2)
Оценка центральной тенденции. 5
3)
Оценка разброса. 5
2.
Корреляционный и регрессионный анализ. 7
3.
Линейная модель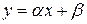 
................ 9
4.
Временной ряд.. 11
Список
литературы... 12
ПРИЛОЖЕНИЯ
Исходные данные
В настоящей работе с помощью программы EXCEL составим описательную
статистику для двух массивов данных – зависимость величины заработной платы (в
рублях) от стажа работы – сотрудников компании ООО «Техномикс-Сервис»,
расположенной по адресу г. Новосибирск, Красный проспект, 50. За массив Х
примем данные о стаже работы, массив Y – величины
заработной платы сотрудников:
Исходные данные:
|
Зарплата
|
Стаж
|
Зарплата
|
Стаж
|
Зарплата
|
Стаж
|
Зарплата
|
Стаж
|
|
4500
|
2
|
7500
|
5
|
6000
|
7
|
4500
|
1
|
|
8000
|
1
|
6000
|
4
|
8000
|
5
|
7000
|
2
|
|
10000
|
5
|
6000
|
7
|
5000
|
4
|
9000
|
1
|
|
7000
|
7
|
10000
|
8
|
9000
|
2
|
7000
|
2
|
|
5000
|
8
|
7500
|
5
|
7500
|
1
|
6500
|
1
|
|
6500
|
2
|
5000
|
4
|
6500
|
2
|
8000
|
2
|
|
6000
|
1
|
6500
|
2
|
9000
|
1
|
5000
|
1
|
|
4500
|
1
|
4500
|
1
|
10000
|
2
|
4500
|
2
|
|
7500
|
4
|
7000
|
4
|
9000
|
1
|
10000
|
1
|
|
6500
|
2
|
7500
|
5
|
5000
|
2
|
8000
|
2
|
Для экономии места в тексте работы таблицу
приведем в четыре столбика, а не в один, как в из EXCEL-файле.
1. Описательная статистика
Описательная статистика
позволяет обобщать первичные результаты, полученные при наблюдении или в
эксперименте. Процедуры здесь сводятся к группировке данных по их значениям,
построению распределения их частот, выявлению центральных тенденций
распределения (например, средней арифметической) и, наконец, к оценке разброса
данных по отношению к найденной центральной тенденции.
1) Группировка данных
Для группировки необходимо прежде всего расположить данные каждой выборки
в возрастающем порядке. Для этого необходимо выделить оба массива данных и нажать
кнопку 
– группировка данных по возрастанию. В
результате получим:
|
Зарплата
|
Стаж
|
Зарплата
|
Стаж
|
Зарплата
|
Стаж
|
Зарплата
|
Стаж
|
|
4500
|
2
|
6000
|
1
|
7000
|
4
|
8000
|
2
|
|
4500
|
1
|
6000
|
4
|
7000
|
2
|
8000
|
2
|
|
4500
|
1
|
6000
|
7
|
7000
|
2
|
9000
|
2
|
|
4500
|
1
|
6000
|
7
|
7500
|
4
|
9000
|
1
|
|
4500
|
2
|
6500
|
2
|
7500
|
5
|
9000
|
1
|
|
5000
|
8
|
6500
|
2
|
7500
|
5
|
9000
|
1
|
|
5000
|
4
|
6500
|
2
|
7500
|
5
|
10000
|
5
|
|
5000
|
4
|
6500
|
2
|
7500
|
1
|
10000
|
8
|
|
5000
|
2
|
6500
|
1
|
8000
|
1
|
10000
|
2
|
|
5000
|
1
|
7000
|
7
|
8000
|
5
|
10000
|
1
|
Первичная группировка состоит в том, что данные о заработной плате
группируются по частотам:
|
Зарплата
|
4500
|
5000
|
6000
|
6500
|
7000
|
7500
|
8000
|
9000
|
10000
|
|
Частота
|
5
|
5
|
4
|
5
|
4
|
5
|
4
|
4
|
4
|
Для наглядности представим данные графически с
помощью гистограммы и полигона частот. Для этого вызовем в Excel Мастер диаграмм по пути
Вставка / Диаграмма. После вызова соответствующих диаграмм получим:
2) Оценка центральной тенденции
Для описания центральной тенденции используются три показателя – мода,
медиана и средняя арифметическая (далее просто средняя).
Мода (Мо) — это самый простой из всех трех показателей. Она
соответствует наиболее частому значению. Медиана – центральное значение в
ранжированном по возрастанию ряде значений заработной платы.
Для вычисления моды в EXCEL выделим массив данных по зарплате и вызовем Вставка / Функция
/ Статистические / МОДА. Аналогично вычислим медиану и среднюю: Вставка /
Функция / Статистические / МЕДИАНА и Вставка / Функция / Статистические /
СРЗНАЧ.
Результат: Мо=4; Ме=7000; М=6937,5.
3) Оценка разброса
Чаще всего для оценки разброса определяют отклонение каждого из полученных
значений от средней, обозначаемое буквой d, а затем вычисляют среднюю
арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных
и тем более разнородна выборка. Напротив, если эта средняя невелика, то данные
больше сконцентрированы относительно их среднего значения и выборка более
однородна.
Итак, первый показатель, используемый для оценки разброса, — это среднее
отклонение. Для его вычисления в Excel вызываем функцию Вставка / Функция / Статистические / СРОТКЛ.
Результат: 1390,625.
Вызовом функции Вставка / Функция / Статистические / КВАДРОТКЛ найдем
квадратичное отклонение. Результат: 113593750.
Вызовом функции Вставка / Функция / Статистические / ДИСП найдем
дисперсию. Результат: 2912660,3
Вызовом функции Вставка / Функция / Статистические / КОРЕНЬ найдем
среднеквадратичное отклонение как квадратный корень из дисперсии. Результат: 1706,6518.
Основной результат вычисления этих описательных статистик то, что большинство
значений (а именно, 68,3% – правило 1s) заработной платы находятся в
диапазоне
6937,5±1706,6518.
2. Корреляционный и регрессионный анализ
Поскольку в настоящей работе исследуем зависимость заработной платы от
стажа, то считаем стаж – независимой переменной, зарплату – зависимой, и
сгруппируем числовые ряды в порядке возрастания стажа:
|
Х - стаж
|
Y - зарплата
|
Х - стаж
|
Y - зарплата
|
Х - стаж
|
Y - зарплата
|
Х - стаж
|
Y - зарплата
|
|
1
|
4500
|
1
|
9000
|
2
|
7000
|
5
|
7500
|
|
1
|
4500
|
1
|
10000
|
2
|
8000
|
5
|
7500
|
|
1
|
4500
|
2
|
4500
|
2
|
8000
|
5
|
7500
|
|
1
|
5000
|
2
|
4500
|
2
|
9000
|
5
|
8000
|
|
1
|
6000
|
2
|
5000
|
2
|
10000
|
5
|
10000
|
|
1
|
6500
|
2
|
6500
|
4
|
5000
|
7
|
6000
|
|
1
|
7500
|
2
|
6500
|
4
|
5000
|
7
|
6000
|
|
1
|
8000
|
2
|
6500
|
4
|
6000
|
7
|
7000
|
|
1
|
9000
|
2
|
6500
|
4
|
7000
|
8
|
5000
|
|
1
|
9000
|
2
|
7000
|
4
|
7500
|
8
|
10000
|
Основными показателями при проведении корреляционного анализа является
коэффициент корреляции.
Вызовом функции Вставка / Функция / Статистические / КОРРЕЛ
найдем коэффициент линейной корреляции между стажем и заработной платы.
Результат: 0.04496. Это число означает, что связь между стажем и зарплатой в
рассматриваемой организации очень слабая – всего 4,496%.
Регрессионный
анализ в Exel
Microsoft
Excel позволяет заполнить ячейки рядом значений, соответствующих простой
линейной или экспоненциальной зависимости. Прогнозируемые значения определяются
на основе начальных данных, указанных на листе. Чтобы экстраполировать данные в
соответствии с линейной зависимостью Microsoft Excel прибавляет или вычитает
постоянную величину, равную разности указанных начальных значений. В случае
экспоненциальной зависимости Microsoft Excel умножает начальные значения на
указанную постоянную величину.
Одной из
встроенных в Excel функций
для регрессивного анализа является функция ПРЕДСКАЗ. Эта функция позволяет
сделать прогноз, применяя линейную регрессию диапазона известных данных или
массивов (x,y). В нашем случае максимальный стаж работы, рассматриваемый в
исходных данных – 8 лет. Спрогнозируем заработную плату сотрудника с
девятилетним стажем работы. Вызовом функции Вставка / Функция / Статистические
/ ПРЕДСКАЗ получим результат: 7149,457 руб.
3. Линейная модель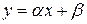
Линейный
регрессионный анализ заключается в подборе графика для набора наблюдений с
помощью метода наименьших квадратов. Регрессия используется для анализа
воздействия на отдельную зависимую переменную значений одной или более
независимых переменных.
В предыдущей
задаче с помощью метода наименьших квадратов (с помощью функции ПРЕДСКАЗ)
выполнялся прогноз заработной платы некоторого сотрудника. В этом пункте в
явном виде получим ту линейную модель, по которой выполняет прогноз функция
ПРЕДСКАЗ. Для наглядности сразу будем представлять процесс прогнозирования в
графическом виде.
Вызываем по
пути Вставка / Диаграмма диаграмму «Точечная».
Затем построим эллипс рассеивания:
Затем с помощью вызова Диаграмма / Добавить линию тренда выбираем
линейный тренд и во вкладке «Параметры» указываем, что нам нужно уравнение
тренда:
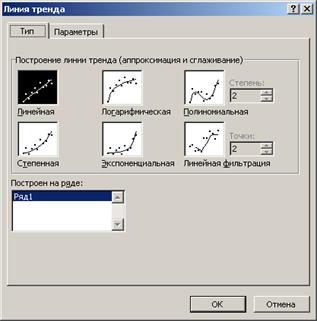
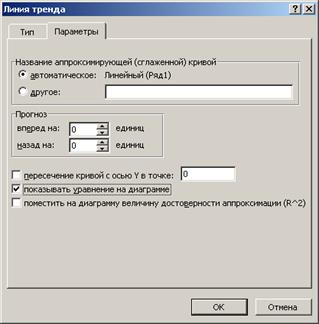
В результате получим линию тренда и уравнение линейной регрессии:
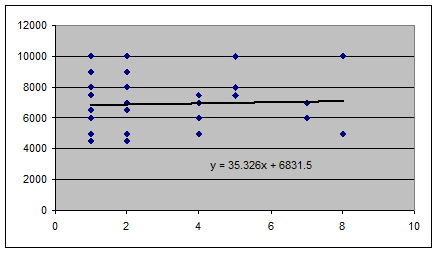
Как видим, линейная модель 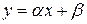в случае нашей задачи
имеет вид:
.
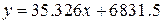Для проверки осуществим прогноз для
х = 9:
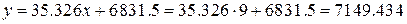руб., что с хорошей
точностью совпадает с прогнозом 7149,457 руб. из предыдущего пункта.
4. Временной ряд
Исследование временных рядов в Excel принципиально не отличается от исследования любых других
массивов данных. Ряды называются временными потому, что одна из переменных (Х
или Y) является временем, и исследуется зависимость какого-нибудь показателя
от времени (его изменение во времени).
Для примера проведем в Excel анализ заработной платы некоторого сотрудника ООО «Техномикс»
в течение 40 месяцев. Месяцы будем нумеровать от 1 до 40. Данные о размере
заработной платы этого сотрудника:
|
Месяцы
|
Зарплата
|
Месяцы
|
Зарплата
|
Месяцы
|
Зарплата
|
Месяцы
|
Зарплата
|
|
1
|
5000
|
11
|
5896
|
21
|
6789
|
31
|
7682
|
|
2
|
5000
|
12
|
5986
|
22
|
6879
|
32
|
7771
|
|
3
|
5300
|
13
|
6075
|
23
|
6968
|
33
|
7861
|
|
4
|
5300
|
14
|
6164
|
24
|
7057
|
34
|
7950
|
|
5
|
5300
|
15
|
6254
|
25
|
7146
|
35
|
8039
|
|
6
|
5500
|
16
|
6343
|
26
|
7236
|
36
|
8129
|
|
7
|
5500
|
17
|
6432
|
27
|
7325
|
37
|
8218
|
|
8
|
5629
|
18
|
6521
|
28
|
7414
|
38
|
8307
|
|
9
|
5718
|
19
|
6611
|
29
|
7504
|
39
|
8396
|
|
10
|
5807
|
20
|
6700
|
30
|
7593
|
40
|
8486
|
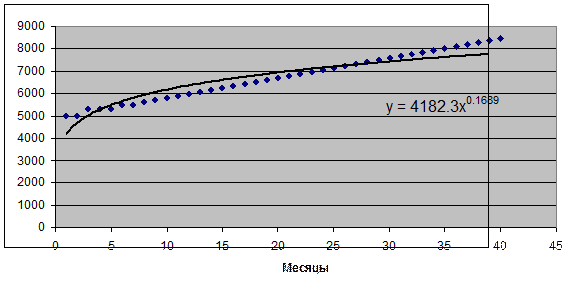
С помощью пакета Excel представим эти данные графически, а также поместим на
диаграмму линию степенного сглаживания и запросим степенное уравнение тренда –
с помощью этого уравнения можно прогнозировать размер заработной платы этого сотрудника
в последующие месяцы его работы.
Список
литературы
1)
Волков
О.И. “Статистические методы исследования”.
Москва. Издательство “ИНФРА” 2001 г.
2)
“Информационные технологии: Учебное пособие”. Под редакцией
Ю.М. Черкасова. Москва. Издательство “ИНФРА-М”. 2002 г.
3)
“Информатика”.
В. А. Острейковский. Москва. Издательство “Высшая школа”. 2002 г.
4)
“Информатика: Учебник”
Под ред. проф. Н.В. Макаровой. Москва. Издательство “Финансы и
статистика”. 1998 г.
5)
“Excel 2000. Учебное пособие”. Под ред.
А. К. Волкова. Москва. Издательство “ИНФРА-М”. 2001 г.
6)
“Эконометрика. Учебное пособие для экономических факультетов”.
Под ред. А.Р. Семенова. Москва. Издательство “Финансы и статистика”. 2000 г.