Профессиональное выполнение дипломных, курсовых работ, рефератов- writer5.ru !

ЗАДАЧА 1 (сводка и группировка)

УСЛОВИЕ ЗАДАЧИ:

Известны данные по десяти крупнейшим рекламодателям в таблице 1.

Таблица 1

Исходные данные задачи 1

№ п/п	Фирма	Общие затраты на рекламу, млн. долл.	Общая сумма продаж, млн. долл.
1	Проктер энд гэмбл	641,7	11944
2	Сирс, Робак энд К ⁰	544,1	27360
3	Дженералс фудз	456,8	8351
4	Филипп Моррис	432,9	10885
5	Дженерал Моторс	401	62698
6	К- Март	349,6	16527
7	Набиско брэндз	340,9	5819
8	Р.Дж. Рейнолдзиндастриз	321,2	11691
9	АТТ	297	58214
10	Мобил	293,1	68587

1. Проранжируйте рекламодателей по удельным затратам на рекламу.

2. Выделите типические группы рекламодателей.

РЕШЕНИЕ:

1) Удельные затраты на рекламу определяются отношением общих затрат на рекламу к общей сумме продаж организации. Результаты расчетов удельным затрат представлены в таблице 2.

Таблица 2

Удельные затраты на рекламу

№ п/п	Фирма	Общие затраты на рекламу, млн. долл.	Общая сумма продаж, млн. долл.	Удельные затраты на рекламу
1	Проктер энд гэмбл	641,7	11944	0,0537
2	Сирс, Робак энд К ⁰	544,1	27360	0,0199
3	Дженералс фудз	456,8	8351	0,0547
4	Филипп Моррис	432,9	10885	0,0398
5	Дженерал Моторс	401	62698	0,0064
6	К- Март	349,6	16527	0,0212
7	Набиско брэндз	340,9	5819	0,0586
8	Р.Дж. Рейнолдзиндастриз	321,2	11691	0,0275
9	АТТ	297	58214	0,0051
10	Мобил	293,1	68587	0,0043

Проранжируем рекламодателей по удельным затратам на рекламу в порядке возрастания в таблице 3.

Таблица 3

Ранжированный ряд рекламодателей по удельным затратам на рекламу

№ п/п	Фирма	Удельные затраты на рекламу
1	Мобил	0,0537
2	АТТ	0,0051
3	Дженерал Моторс	0,0064
4	Сирс, Робак энд К ⁰	0,0199
5	К- Март	0,0212
6	Р.Дж. Рейнолдзиндастриз	0,0275
7	Филипп Моррис	0,0398
8	Р.Дж. Рейнолдзиндастриз	0,0537
9	Дженералс фудз	0,0547
10	Набиско брэндз	0,0586

2) Для выделения типических групп по общей сумме продаж определим величину интервала по формуле (1):

x_i = (x_max-x_min +1)/(1+3,322 lg10), (1)

x_i = (68587-5819+1)/(1+3,322 lg10) = 14523.

Выделяем интервалы и определяем количество фирм, попавших в эти интервалы в таблице 4

Таблица 4

5819-20342	6
20343-34866	1
34867-49390	0
49391-63914	2
63915-78438	1

Таким образом, наибольшее число фирм попало в первый интервал от 5819 до 20342 млн. руб.

ЗАДАЧА № 2 (ряды динамики)

УСЛОВИЕ ЗАДАЧИ:

Имеются данные о потерях рабочего времени на предприятии вследствие заболеваемости с временной утратой трудоспособности в таблице 5

Таблица 5

Исходные данные задачи № 2

Годы	Потери рабочего времени, дни
1	933,4
2	904,0
3	965,0
4	1014,1
5	1064,8
6	1122,9

1) Для определения тенденции проведите аналитическое выравнивание (подберите вид аналитической функции);

2) Отобразите фактические и теоретические (сглаженные) уровни ряда на графике. Покажите ожидаемые уровни ряда на следующие 2- 3 года, сделайте выводы.

РЕШЕНИЕ:

1) Принимаем величину «годы» за переменную х, а величину потерь рабочего времени за переменную y. Тогда значения х_ср и y_ср определяем по формулам (2) и (3):

х_ср = (Σ x_i) / n, (2)

y_ср = (Σ y_i) / n, (3)

где n = 6,

i = 1…6

Тогда, х_ср = 21 : 6 = 3,5

y_{ср =} 6004,2 :6 = 1000,7

2) Дальнейшие результаты расчета представляем в виде таблицы 6

Таблица 6

x_i - х_ср	(x_i - х_ср)²	(x_i y_i_-x_i y_ср)²	(y_i - y_ср)	(y_i - y_ср)²	(x_i - х_ср)( y_i - y_ср)
-2,5	6,25	4529,29	-67,3	4529,29	168,25
-1,5	2,25	37403,56	-96,7	9350,89	145,05
-0,5	0,25	11470,41	-35,7	1274,49	17,85
0,5	0,25	2872,96	13,4	179,56	6,7
1,5	2,25	102720,25	64,1	4108,81	96,15
2,5	6,25	537582,24	122,2	14932,84	305,5
	17,5			34375,88	739,5

Σ(x_i - х_ср)² = 17,5

Σ(y_i - y_ср)² = 34375,88

Σ(x_i - х_ср)( y_i - y_ср) = 739,5

3) Теснота связи между показателями измеряется коэффициентом корреляции, который исчисляется по формуле (4):

V = δ²_xy / δ_x· δ_y, (4)

где V – коэффициент корреляции,

δ_x = [Σ(x_i - х_ср)²/ n]^1\2, (5)

δ_y = [Σ(y_i - y_ср)²/ n]^1\2, (6)

δ²_xy = 1/n ∑ (x_i - х_ср)( y_i - y_ср), (7)

Подставляя имеющиеся значения в формулы (5),(6),(7),получаем:

δ_y = (34375,88/6)^1/2 = (5729,31)^1/2 = 75,69

δ_x = (17,5/6)^1/2 = (2,92)^1/2 = 1,71

δ²_xy = 739,5/6 = 123,25

Тогда, значение коэффициента корреляции равно:

V = 123,25/ (75,69· 1,71) ≈ 0,952

4) Считая формулу связи между показателями линейной (y = a₀ + a₁x), определим зависимость. Для этого решается система нормальных уравнений:

na₀ + a₁∑x_i = ∑y_i, (8)

a₀∑x_i+a₁∑x_i² = ∑ x_i y_i, (9)

Величины ∑x_i² и ∑ x_i y_i представлены в таблице 7.

Таблица 7

x_i²	1	4	9	16	25	36	∑x_i² = 91
x_i y_i	933,4	1808	2895	4056,4	5324	6737,4	∑ x_i y_i = 21754,2

Значение a₀ определяем из формулы (8):

6 a₀ + 21 a₁ = 6004,2,

6 a₀= 6004,2 –21 a₁

a₀ = (6004,2 – 21 a₁)/ 6,

или a₀ = 1000,7 – 3,5 a₁

Подставляя найденное значение a₀ в формулу (9), находим значение a₁:

21 (1000,7 – 3,5 a₁) + 91 a₁ = 21754,2

21014,7 – 73,5 a₁ + 91 a₁ = 21754,2

17,5 a₁ = 739,5

a₁ = 42,26

Тогда, a₀ = 1000,7 – 3,5 * 42,26 = 852,79.

Итак, уравнение регрессии в окончательном виде имеет следующий вид:

y_ср = 852,79 + 42,26 · x_ср

5) Сделаем прогноз значений потерь рабочего времени на 7, 8 и 9 годы. Для этого подставляем значения х в полученное уравнение регрессии:

у _{7 год} = 852,79 + 42,26* 7 = 1148,61

у _{8 год} = 852,79+42,26*8 = 1190,87

у _{9 год} = 852,79 + 42,26*9 = 1233,13

6) Построим график с изображением фактических и теоретических уровней ряда на рисунке 1 и 2.

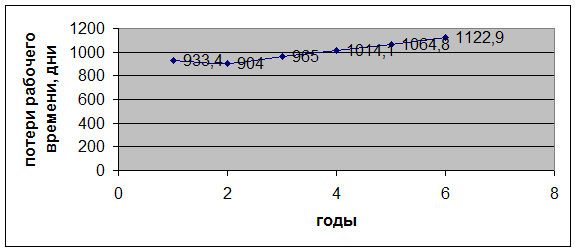
Рис. 1. Фактические уровни ряда

Рис.2.Теоретические уровни ряда

ВЫВОДЫ:

Как видно по результатам расчетов была выявлена линейная аналитическая функция для значения потерь рабочего времени по годам, которая представлена выражением: y_ср = 852,79 + 42,26 · x_ср.

Согласно выявленной зависимости был сделан прогноз значений потерь рабочего времени на ближайшие 3 года, который свидетельствует о тенденции роста показателя потерь в перспективе.

ЗАДАЧА № 3 (выборка)

УСЛОВИЕ ЗАДАЧИ:

Анализ 10 % банковских счетов, выделенных в результате бесповторного собственно- случайного отбора, показал следующее распределение, представленное в таблице 8.

Таблица 8

Исходные данные задачи № 3

Размер вклада, тыс. руб.	до 1	1-5	5-10	10-15	15 и более
Количество вкладов, %	20	25	40	10	5

Определите средний размер вклада, и , с вероятностью р = 0,954, установите его возможные пределы для всей совокупности вкладов населения.

РЕШЕНИЕ:

1) Для определения средней величины вклада интервального вариационного ряда сделаем переход от интервального ряда к дискретному, при котором за значение интервала принимается его середина. Результаты расчетов представлены в таблице 9.

Таблица 9

Расчет среднего размера вклада

размер вклада	количество вкладов	x_i	x_i-x₀	x_i-x₀/к	м'	(xi-x0/к)*м'
0-1	20	0,5	-9,5	-1,9	4	-7,6
1-5	25	3	-7	-1,4	5	-7
5-10	40	7,5	-2,5	-0,5	8	-4
10-15	10	12,5	2,5	0,5	2	1
15-20	5	17,5	7,5	1,5	1	1,5
Итого	100				20	-16,1

В качестве х₀ в таблице 9 взято условное начало, которое определяется по формуле (10):

х₀ = (х _мах + х _мин) /2, (10)

где х _мах = 0

х _мин = 20

Тогда х₀ = (0+20)/2 = 10.

Значение к есть величина интервала. Она равна 5.

Значение м’ определяется по формуле (11):

м’ = q / к, (11)

где q – количество вкладов

Далее определяем значение М по формуле (12):

, (12)

Подставляя значения в формулу (12), получим:

М = -16,1 /20 = -0,805

По формуле (13) определяем среднее значение вклада:

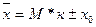, (13)

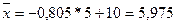
Таким образом, средний размер вклада равен 5,975 тыс. руб.

2)Определим возможные пределы для всей совокупности вкладов с вероятностью р = 0,954.

При выборке объема n= 5, среднем значении 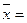5,975 и вероятности 0,954, определим значение среднего квадратического отклонения от средней σ по формуле (14):

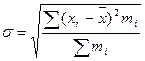, (14)

Таблица 10

x_i	m_i	x_i-x_ср	(x_i-x_ср)²	(x_i-x_ср)²*м_i
0,5	20	-5,48	29,98	599,5
3	25	-2,98	8,851	221,3
7,5	40	1,525	2,326	93,03
12,5	10	6,525	42,58	425,8
17,5	5	11,53	132,8	664,1
	100			2004

Тогда,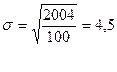

По таблице интегральной функции Лапласа находим, что:

Ф(х_р)=р /σ=0,954/4,5=0,212

Отсюда, х_р= 1,96

Найдем значение Δ по формуле (15):

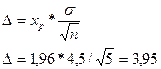, (15)

Возможные пределы для всей совокупности вкладов населения определим следующим образом:

(х_ср – Δ; х_ср + Δ), (16)

Подставляя имеющиеся значения в формулу (16), получим:

(2,025;9,925)- возможные пределы для всей совокупности вкладов.

ЗАДАЧА № 4 (взаимосвязи)

УСЛОВИЕ ЗАДАЧИ:

Установите, имеется ли взаимосвязь между показателями «Состав семьи» и «Успеваемость ребенка», используя критерий χ².

Таблица 11

Исходные данные задачи № 4

Состав семьи	Успеваемость ребенка в школе	Итого
неудовлетв.	удовлетвор.	хорошо	отлично
сирота	10	60	18	27	115
неполная семья	8	38	40	30	116
полная семья	3	26	40	38	107
всего	21	124	98	95	338

РЕШЕНИЕ:

Если указанные показатели являются зависимыми, то должно соблюдаться условие:

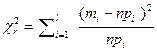, (17)

где r = l-m-1,

m – количество параметров распределения, оцененных по выборке, оно равно 2.

l – количество интервалов, оно равно 4.

Тогда, r = 4-2-1 = 1.

m_i – фактическое попадание на интервал

n – объем выборки, он равен 338.

p_i – вероятность попадания каждого значения на интервал.

Для расчетов будем использовать данные таблицы 12,13, 14.

Таблица 12

Расчет наблюдаемого значения критерия Пирсона для показателя «Сироты»

№ интервала Интервал	Границы интервала	m_i	р_i	np_i	m_i-npi	(m_i-np_i)²	(m_i-np_i)²/np_i
1	(1;2) неудовл.	10	10/115=0,087	10,01	0,00	0,0000250	0,0000025
2	(2;3) удовл	60	60/115=0,522	60,03	-0,03	0,0009000	0,0000150
3	(3;4) хорошо	18	18/115=0,157	18,06	-0,05	0,0030250	0,0001675
4	(4;5) отлично	27	27/115=0,235	27,03	-0,02	0,0006250	0,0000231
		115	1	115,12	-0,115	0,0132250	0,0002082

Таким образом, для показателя «Сироты» наблюдаемое значение критерия Пирсона равно 0,0002082. По таблице «Значения критерия Пирсона» определяем χ² при числе степеней свободы 2 и средней вероятности попадания равной 0,34. Это значение равно 2,41. Так как неравенство (17) не соблюдается, то делаем вывод, что показатели «Сирота» и «Успеваемость ребенка» независимы.

Аналогичные расчеты проводим для других значений показателя «Состав семьи»

Таблица 13

Расчет наблюдаемого значения критерия Пирсона для показателя «Неполная семья»

№ интервала Интервал	Границы интервала	mi	р_i	np_i	m_i-np_i	(m_i-np_i)²	(m_i-np_i)²/np_i
1	(1;2) неудовл.	8	8/116=0,069	8,00	0,00	0,0000160	0,0000020
2	(2;3) удовл	38	38/116=0,328	38,05	-0,05	0,0023040	0,0000606
3	(3;4) хорошо	40	40/116=0,345	40,02	-0,02	0,0004000	0,0000100
4	(4;5) отлично	30	30/116=0,259	30,04	-0,04	0,0019360	0,0000644
		116	1	116,12	-0,116	0,0134560	0,0001370

Наблюдаемое значение критерия Пирсона равно 0,0001370.

Таблица 14

Расчет наблюдаемого значения критерия Пирсона для показателя «Полная семья»

№ интервала Интервал	Границы интервала	m_i	р_i	np_i	m_i-np_i	(m_i-np_i)²	(m_i-np_i)²/np_i
1	(1;2) неудовл.	3	3/107=0,028	3,00	0,00	0,0000160	0,0000053
2	(2;3) удовл	26	26/107=0,243	26,00	0,00	0,0000010	0,0000000
3	(3;4) хорошо	40	40/107=0,374	40,02	-0,02	0,0003240	0,0000081
4	(4;5) отлично	38	38/107=0,355	37,99	0,02	0,0002250	0,0000059
		107	1	107,00	0	0,0000000	0,0000194

Наблюдаемое значение критерия Пирсона рано 0,0000194.

ВЫВОДЫ: Исходя из проведенных расчетов можно сделать вывод, что показатели «Состав семьи» и «Успеваемость ребенка» независимы друг от друга.

ЗАДАЧА № 5 (индексы)

УСЛОВИЕ ЗАДАЧИ:

Имеются данные по предприятиям отрасли в таблице 15

Таблица 15

Исходные данные задачи № 5

Предприятие	Среднегодовая стоимость производственных фондов, тыс. руб.	Прибыль, тыс. руб.
предыдущий год	отчетный год	предыдущий год	отчетный год
1	9000	10800	1800	2000
2	6400	6800	1520	1640

Определите:

1) индексы рентабельности производства для каждого предприятия в отдельности (индивидуальные индексы);

2) индекс общего среднего уровня рентабельности производства (индекс переменного состава);

3) индекс общей рентабельности производства постоянного (фиксированного состава), поясните его отличие от индекса переменного состава.

РЕШЕНИЕ:

1) Рентабельность производства есть отношение прибыли к среднегодовой стоимости производственных фондов.

Индивидуальный индекс рентабельности производства рассчитывается как отношение рентабельности производства отчетного периода к предыдущему году по соответствующему предприятию.

Таблица 16

Рентабельности производства по предприятиям

Предприятие	Среднегодовая стоимость производственных фондов, тыс. руб.	Прибыль, тыс. руб.	Рентабельность, %
предыдущий год	отчетный год	предыдущий год	отчетный год	предыдущий год	отчетный год
С₀	С₁	П₀	П₁	Р₀=П₀/С₀	Р₁=П₁/С₁
1	9000	10800	9000	10800	20	18,52
2	6400	6800	6400	6800	23,75	24,12

Индивидуальные индексы:

- предприятие № 1: iр= 18,52/20=0,926

- предприятие № 2: iр = 24,12/23,75=1,016

Как видно, индивидуальный индекс по предприятию № 1 показывает, что рентабельность производства упала, по предприятию № 2 рентабельность производства выросла.

2) Со стоимостными показателями используем веса отчетного периода. Со измерителем возьмем среднегодовую стоимость производственных фондов.

Индекс переменного состава определяется по формуле (17)

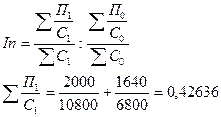, (17)

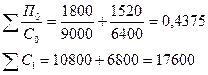
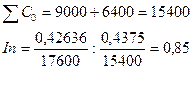
Таким образом, значение индекса переменного состава свидетельствует о снижении общего среднего уровня рентабельности производства.

3) Индекс постоянного состава определяем по формуле (18)

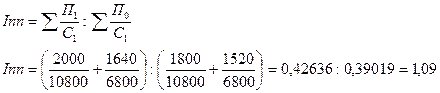, (18)

Таким образом, индекс постоянного состава свидетельствует о росте значения общей рентабельности производства на 9 %.

Индекс постоянного состава в отличие от индекса переменного состава показывает влияние на показатель рентабельности изменения только значения стоимости производственных фондов.