Министерство образования Российской Федерации
Всероссийский заочный финансово-экономический институт
КУРСОВАЯ РАБОТА
по статистике
на тему
“ Корреляционно-регрессионный анализ в экономических
исследованиях”
Студент 3-го курса:
группа:
специальность:
личное дело:
руководитель:
Челябинск
2005
Оглавление
Введение………………………………………………………………….....2
Теоретическая часть……………………………………………………......4
1. Взаимосвязанные признаки и
графики связи………………………4
2. Виды связей между
признаками…………………………………….6
3. Уравнение
регрессии………………………………………………...8
4. Корреляционная
таблица……………………………………..……13
5. Эмпирическое корреляционное
отношение………………………15
6. Коэффициент линейной
корреляции и индекс корреляции……..17
7. Множественная
корреляция…………………………………….….19
Расчетная часть……………………………………………………………20
Аналитическая
часть………………………………………………………25
Заключение………………………………………………………………...30
Список использованной
литературы………………………………….….31
Введение
Обработка статистических данных уже давно
применяется в самых разнообразных
видах человеческой деятельности. Вообще говоря, трудно назвать ту сферу, в которой
она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической
деятельности обработка статистических данных
не играет такой исключительно большой роли, как в экономике, имеющей
дело с обработкой и анализом огромных массивов информации о
социально-экономических явлениях и процессах. Всесторонний и глубокий анализ
этой информации, так называемых статистических данных, предполагает
использование различных специальных методов, важное место среди которых
занимает корреляционный и регрессионный анализы обработки статистических
данных, поэтому тема моей курсовой работы очень актуальна.
В экономических исследованиях часто решают задачу выявления
факторов, определяющих уровень и динамику экономического процесса. Такая задача
чаще всего решается методами корреляционного и регрессионного анализа. Для
достоверного отображения объективно существующих в экономике процессов
необходимо выявить существенные взаимосвязи и не только выявить, но и дать им
количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под
причинной зависимостью понимается такая связь между процессами, когда изменение
одного из них является следствием изменения другого.
Основными задачами корреляционного анализа являются оценка
силы связи и проверка статистических гипотез о наличии силе корреляционной
связи. Не все факторы, влияющие на экономические процессы, являются случайными
величинами, поэтому при анализе экономических явлений обычно рассматриваются
связи между случайными и неслучайными величинами. Такие связи называются регрессионными,
а метод математической статистики, их изучающий, называется регрессионным
анализом.
Использование возможностей современной вычислительной
техники, оснащенной пакетами программ машинной обработки статистической
информации на ЭВМ, делает практически осуществимым оперативное решение моей задачи
изучения связи между размером среднегодовой стоимости основных производственных
фондов и выпуском продукции в расчетной части курсовой работы.
При машинной обработке исходной информации на ЭВМ, оснащенных
пакетами стандартных программ ведения анализов, вычисление параметров
применяемых математических функций является быстро выполняемой счетной
операцией.
Для полного усвоения корреляционно-регрессионного анализа в
экономических исследованиях в аналитической части работы будет приведено еще
одно решение задачи.
Данная работа посвящена изучению возможности обработки
статистических данных методами корреляционного и регрессионного анализа с использованием
пакета прикладных программ Microsoft Excel.
Взаимосвязанные признаки и графики
связи
Марксистко-ленинская
философия учит, что существует всеобщая связь явлений, представляющая собой
результат универсального взаимодействия всех предметов и явлений.
При рассмотрении влияния
одних признаков явлений на другие из цепи признаков, характеризующих данное
явление, выделяются признаки факторные и результативные. Выделение признаков
производится прежде всего при помощи логического анализа. Например,
производительность труда рабочих зависит от многих факторов, в том числе и от
стажа работы этих рабочих. Производительность труда выступает здесь как
результативный признак, а стаж работы называется функцией, факторный -
аргументом.
Наиболее простым методом
оценки связи двух или нескольких признаков является метод группировки, при
котором факторные признаки являются основанием группировки.
Статистическую связь
между двумя признаками можно изобразить графически. Для этой цели в математике
результативный признак принято обозначать через 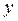 , факторный признак – через
, факторный признак – через 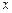 . Имея численные значения обоих признаков, можно каждую пару
чисел, относящуюся к определенной единице совокупности, графически представить
на плоскости, образуемой системой прямоугольных координат, в виде точки.
Согласно правилам математики по оси абсцисс откладываются значения факторного
признака, а по оси ординат – результативного. Соединив полученные точки прямыми
линиями, в итоге получаем ломаную, которую называют ломаной регрессии. Число
точек ломаной регрессии зависит от числа единиц, по которым даны значения обоих
признаков.
. Имея численные значения обоих признаков, можно каждую пару
чисел, относящуюся к определенной единице совокупности, графически представить
на плоскости, образуемой системой прямоугольных координат, в виде точки.
Согласно правилам математики по оси абсцисс откладываются значения факторного
признака, а по оси ординат – результативного. Соединив полученные точки прямыми
линиями, в итоге получаем ломаную, которую называют ломаной регрессии. Число
точек ломаной регрессии зависит от числа единиц, по которым даны значения обоих
признаков.
График связи можно применить
лишь при иллюстрации зависимости между двумя признаками, т. е., как говорят,
при парной корреляции. При графическом изображении связи между несколькими
взаимосвязанными признаками используется метод графов. Метод графов не
позволяет судить о форме связи между признаками, а дает возможность графически
представить, какие из факторов влияют на результативный признак, а также
взаимосвязи факторных признаков. Граф представляет собой точки(вершины),
соединенные линиями(ребрами).
Виды связей между признаками
В статистике взаимосвязь
явлений изучается методом корреляции. Основоположниками теории корреляции
считаются английские биометрики Ф. Гальтон (1822-1911 гг.) и К. Пирсон
(1857-1936 гг.).
Всеобщая связь явлений
составляет внутреннее структурное единство всех элементов и свойств в каждой
целостной системе. Всеобщая связь явлений имеет бесконечное разнообразие
проявлений. Связи могут быть существенными и несущественными, прямыми и
косвенными, функциональными и статистическими. Всеобщая связь явлений тесно связана
с причинностью, однако причина и следствие, как таковые, могут рассматриваться
лишь вне универсальной связи одних явлений с другими.
Связь называется функциональной, если
изменение одних явлений вызывает вполне определенное изменение других. Такие
связи проявляются в виде закона, который обладает точной количественной
определенностью и может быть, в принципе, выражен в форме уравнения. Так,
площадь круга зависит от квадрата его радиуса. Площадь круга в этом случае
является функцией радиуса круга (аргумента). Таким образом, при функциональных
связях факторный признак полностью определяет величину результативного
признака.
В массовых явлениях
общественной жизни функциональные связи встречаются реже. Эти явления
отличаются сложностью и многообразием существующих и проявляющихся между ними
взаимосвязей. Стохастической называется связь между случайными величинами. Эта
связь проявляется в том, что изменение одной величины вызывает изменение
распределения другой, связанной с ней случайной величиной. Частным случаем
стохастических связей являются статистические.
Итак, связи, возникающие при
большом числе наблюдений и проявляющиеся в том, что изменение среднего значения
одного признака приводит в общем и в целом к изменению среднего значения
другого признака, называются связями статистическими. Статистические связи
подразделяются на связи корреляционные и регрессионные. Величины называются
корреляционно связанными, если изменение математического ожидания одной из них
изменяет математическое ожидание другой, при этом оба взаимосвязанных признака
должны выражаться случайными величинами. Регрессионные связи выражают
зависимость между случайными и неслучайными величинами. Результативными
признаками здесь являются случайные величины, а факторными – неслучайные величины.
Уравнение регрессии
Уравнение, отображающее
статистическую связь между признаками, называется уравнением регрессии. Если
уравнение регрессии связывает лишь два признака, то оно называется уравнением
парной регрессии или уравнением регрессии одного фактора. Если уравнение связи
отражает зависимость результативного признака от двух или более факторных
признаков, оно называется уравнением множественной регрессии.
При определении вида уравнения парной
регрессии используют, главным образом, графическое изображение статистической
связи. Полученная ломаная регрессии дает исследователю возможность определить,
какую функцию надо применить для отображения связи.
Геометрически уравнение регрессии
видоизменяется при парной регрессии, как прямая или кривая линия, при
множественной регрессии - как гиперповерхность (в линейной связи –
гиперплоскость) в (n+1)-мерном пространстве, вокруг которой рассеяны
фактические данные.
Прямая связь, при которой результативный
признак изменяется по арифметической прогрессии, а факторный – более быстро
требует применения параболической или показательной регрессии. Уравнение
множественной регрессии часто выражают прямой, зависящей от многих переменных,
или степенной функцией.
Определить уравнение регрессии означает найти его параметры.
При этом обычно применяют правило наименьших квадратов, согласно которому сумма
квадратов отклонений фактических значений результативного признака (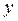 ) от его значений, найденных по уравнению регрессии (
) от его значений, найденных по уравнению регрессии (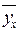 или
или 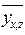 , или
, или 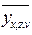 и т. д.) должна быть
наименьшей:
и т. д.) должна быть
наименьшей:
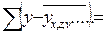 min
min
Это выражение после дифференцирования
превращается в систему нормальных уравнений, решение которой позволяет
определить параметры уравнения регрессии. Всегда число нормальных уравнений на
одно больше числа входящих в уравнение регрессии независимых переменных.
Доказано, что уравнение регрессии
отражает связь между признаками более точно, если оно построено на основании
достаточно большого числа наблюдений для однородной совокупности экономических
явлений. Поскольку оно выражает приближенную связь, его часто называют моделью
связи между явлениями.
Линейная регрессия одного фактора
Уравнение линейной регрессии
одного фактора записывается в виде уравнения прямой: 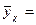
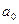 +
+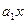 , где
, где 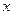 - факторный признак;
- факторный признак; 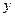 - результативный признак;
- результативный признак; 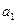 и
и 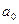 - параметры уравнения. Чтобы определить параметры пользуются
методом наименьших квадратов и находят минимум функций S= Σ (
- параметры уравнения. Чтобы определить параметры пользуются
методом наименьших квадратов и находят минимум функций S= Σ (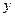 -
- 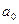 -
-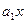 )
)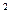 . В этой функции за переменные принимаются последовательно
значения
. В этой функции за переменные принимаются последовательно
значения 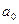 и
и 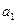 . Экстремум функции двух переменных определяется, если
приравнять частные производные по этим переменным нулю.
. Экстремум функции двух переменных определяется, если
приравнять частные производные по этим переменным нулю.
После определения частных производных функции
по 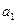 и
и 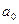 , приравнивания их нулю, и небольших преобразований получим
систему нормальных уравнений:
, приравнивания их нулю, и небольших преобразований получим
систему нормальных уравнений:
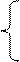

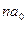 +
+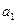 Σ
Σ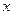 = Σ
= Σ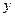 ;
;
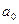 Σ
Σ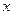 +
+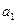 Σ
Σ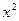 = Σ
= Σ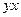 ,
,
Решение которой и позволяет определить
величины параметров 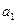 и
и 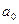 , а следовательно и уравнение регрессии.
, а следовательно и уравнение регрессии.
Параметры уравнения линейной регрессии
одного фактора можно находить и по формулам:
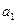 =
=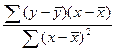 ;
; 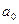 =
=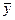 -
- 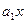 .
.
Ясно,
что практически приемлемым является наименее трудоемкий вариант расчета. В
уравнении прямой параметр 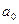 экономического смысла
не имеет. Параметр
экономического смысла
не имеет. Параметр 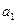 является коэффициентом
регрессии и показывает изменение результативного признака при изменении
факторного признака на единицу.
является коэффициентом
регрессии и показывает изменение результативного признака при изменении
факторного признака на единицу.
Кроме линейной функции связи в
экономическом анализе часто применяются степенная, гиперболическая и
параболическая функции.
Расчет параметров степенной функции
Если значения факторного признака
расположены в порядке геометрической прогрессии и соответствующие значения
результативного признака также образуют геометрическую прогрессию, то связь
между признаками может быть представлена степенной функцией вида
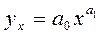
Для определения параметров степенной
функции методом наименьших квадратов необходимо привести ее к линейному виду
путем логарифмирования:
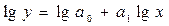 .
.
Система нормальных уравнений имеет вид:
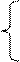
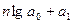 Σ
Σ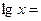 Σ
Σ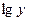 ,
,
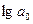 Σ
Σ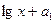 Σ
Σ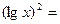 Σ
Σ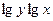 .
.
Параметры можно определить, решая систему
нормальных уравнений или по формулам:
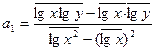 ,
, 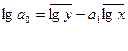 .
.
Расчет параметров уравнения
гиперболы
Если результативный признак с увеличением
факторного признака возрастает (или убывает) не бесконечно, а стремится к
конечному пределу, то для анализа такого признака применяется уравнение гиперболы
вида
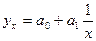 .
.
Для определения параметров этого уравнения
используется система нормальных уравнений
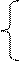 Σ
Σ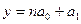 Σ
Σ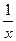 ,
,
Σ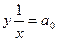 Σ
Σ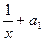 Σ(
Σ(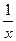 )
)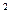 .
.
Чтобы определить параметры уравнения
гиперболы методом наименьших квадратов, необходимо привести его к линейному
виду. Для этого произведем замену переменных 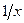 =
=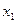 , получим следующую систему нормальных уравнений:
, получим следующую систему нормальных уравнений:
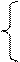 Σ
Σ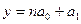 Σ
Σ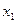 ,
,
Σ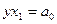 Σ
Σ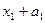 Σ
Σ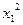 .
.
Параметры уравнения гиперболы можно
вычислить по формулам
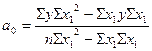 ,
,
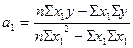 .
.
Параболическая регрессия
одного фактора
Связь одного фактора, при которой
результативный признак увеличивается быстрее, чем факторный, отображается
уравнением параболы второго порядка: 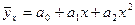 . Для определения параметров параболы по методу наименьших
квадратов находят минимум функции
. Для определения параметров параболы по методу наименьших
квадратов находят минимум функции 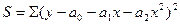 .
.
При этом получают следующую систему
нормальных уравнений:
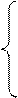
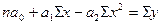 ;
;
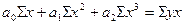 ;
;
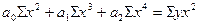 .
.
Первое уравнение почти полностью
воспроизводит само уравнение параболы, второе уравнение старше первого на 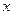 , третье - старше первого на
, третье - старше первого на 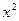 .
.
Корреляционная таблица
Парная таблица с большим
числом наблюдений часто становится мало обозримой, и по ней неудобно вести
расчеты. Поэтому для табличного изображения парной связи, решения уравнения
регрессии и определения показателей тесноты связи используют корреляционную
(двумерную) таблицу. В корреляционной таблице можно отобразить только парную
связь, т. е. связь результативного признака с одним фактором. Она позволяет
найти уравнение регрессии и вычислить линейный коэффициент корреляции. Само
уравнение регрессии может иметь линейную, параболическую, гиперболическую,
показательную и др. формы. При нахождении уравнения регрессии и линейного
коэффициента по корреляционной таблице не теряется информация о связи,
обусловленная усреднением данных. В корреляционной таблице связь между
признаками выступает более рельефно, чем при рассмотрении средних значений
факторного и результативного признаков. Однако, если обеспечивается возможность
счета по каждой паре взаимосвязанных данных, необходимо ею воспользоваться и
прибегать к корреляционной таблице лишь в отдельных случаях – при группировке
данных.
Для составления
корреляционной таблицы парной связи материал предварительно группируется по
обоим признакам. Затем строится таблица, в которой по строкам откладываются
группы одного (например, результативного) признака, а по столбцам размещаются
группы другого (теперь факторного) признака. В клетках этой таблицы отмечается
число единиц, имеющих определенную величину того и другого признаков. Итоги по
строкам (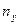 ) покажут число единиц в каждой группе результативного
признака (если он размещен в строках). Итоги по колонкам (
) покажут число единиц в каждой группе результативного
признака (если он размещен в строках). Итоги по колонкам (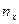 ) покажут распределение факторного признака. В клетке, в
которой итоги по строке сходятся с итогами по колонке, получаем число
наблюдений:
) покажут распределение факторного признака. В клетке, в
которой итоги по строке сходятся с итогами по колонке, получаем число
наблюдений: 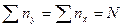 .
.
Корреляционная
зависимость задается таблицей:
Таблица 1
|
 х у х у
|
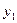
|
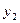
|
…
|
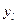
|
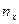
|
|
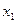
|
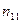
|
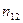
|
…
|
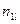
|
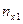
|
|
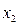
|
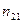
|
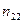
|
…
|
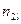
|
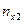
|
|
…
|
…
|
…
|
…
|
…
|
…
|
|
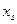
|
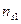
|
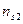
|
…
|
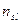
|
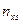
|
|
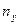
|
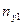
|
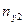
|
…
|
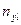
|
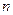
|
Корреляционная таблица дает общее
представление о направлении связи. Когда оба признака расположены в
возрастающем порядке, числа предприятий в клетках сосредотачиваются в
направлении диагонали слева направо, что указывает на прямую связь между
признаками. Все числа предприятий сосредотачиваются в эллипсе, вытянутом по
этой диагонали, называемом корреляционным эллипсом. Чем более сжат этот эллипс,
тем кучнее частоты располагаются около его диагонали, тем теснее связь между
признаками.
Эмпирическое корреляционное отношение
Теснота или сила связи между
двумя признаками может быть измерена показателем, называемым эмпирическим
корреляционным отношением. Этот показатель назван эмпирическим, поскольку он
может быть рассчитан на основе обычной группировки по факторному и
результативному признаку, то есть на основе корреляционной таблицы.
Эмпирическое корреляционное отношение получается из правила сложения дисперсий,
согласно которому 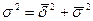 , где
, где 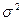 - общая дисперсия;
- общая дисперсия; 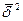 - межгрупповая дисперсия;
- межгрупповая дисперсия; 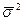 - внутригрупповая (средняя из частных) дисперсия.
Межгрупповая дисперсия является мерой колеблемости, обусловленной факторным
признаком. Средняя из частных дисперсий является мерой колеблемости,
обусловленной всеми остальными(кроме факторного) признаками. Тогда отношение
- внутригрупповая (средняя из частных) дисперсия.
Межгрупповая дисперсия является мерой колеблемости, обусловленной факторным
признаком. Средняя из частных дисперсий является мерой колеблемости,
обусловленной всеми остальными(кроме факторного) признаками. Тогда отношение 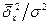 выражает долю колеблемости,
возникающей за счет факторного признака, в общей колеблемости. Квадратный
корень из этого отношения и называется эмпирическим корреляционным отношением:
выражает долю колеблемости,
возникающей за счет факторного признака, в общей колеблемости. Квадратный
корень из этого отношения и называется эмпирическим корреляционным отношением: 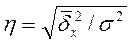 .
.
Отсюда следует правило, что
чем больше межгрупповая дисперсия, тем сильнее факторный признак влияет на
вариации результативного признака. Составляющие отношения дисперсий вычисляются
по данным корреляционной таблицы по следующим формулам:
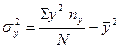 ;
; 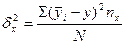 ,
,
где 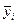 - частные средние;
- частные средние; 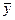 - общая средняя;
- общая средняя; 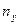 - итоги по признаку
- итоги по признаку 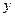 ;
; 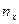 - итоги по признаку
- итоги по признаку 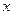 ;
; 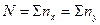 - число наблюдений. То
же соотношение сохраняется и для условных значений
- число наблюдений. То
же соотношение сохраняется и для условных значений 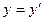 , полученных числовым преобразованием
, полученных числовым преобразованием 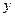 .
.
Само отношение дисперсий
(подкоренное выражение) называется коэффициентом детерминации (оно равно также
квадрату эмпирического корреляционного отношения). Эмпирическое корреляционное отношение
изменяется в широких пределах (от 0 до 1). Если оно равно нулю, значит
факторный признак на корреляционный не влияет. Если 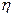 =1, значит, результативный признак полностью зависит от
факторного. Если же эмпирическое корреляционное отношение представляет дробь,
близкую единице, то говорят о тесной связи между факторным и результативным
признаками. Если эта дробь мала (близка нулю), то говорят о слабой связи между
ними.
=1, значит, результативный признак полностью зависит от
факторного. Если же эмпирическое корреляционное отношение представляет дробь,
близкую единице, то говорят о тесной связи между факторным и результативным
признаками. Если эта дробь мала (близка нулю), то говорят о слабой связи между
ними.
Коэффициент линейной корреляции и
индекс корреляции
Мерой тесноты связи между
двумя статистически связанными признаками служит коэффициент линейной
корреляции или просто коэффициент корреляции. Он имеет тот же смысл, что и
эмпирическое корреляционное отношение, но может принимать как положительное,
так и отрицательное значение. Коэффициент корреляции имеет строгое
математическое выражение для линейной связи. Положительное значение будет
указывать на прямую связь между признаками, отрицательное – на обратную.
Парный
коэффициент корреляции в случае линейной формы связи вычисляют по формуле
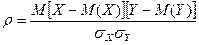 ,
,
а его выборочное значение – по формуле 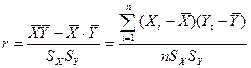
При
малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по
следующей формуле:
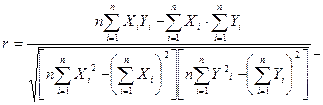
Величина
коэффициента корреляции изменяется в интервале 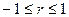 .
.
При
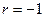 между двумя
переменными существует функциональная связь, при
между двумя
переменными существует функциональная связь, при 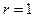 - прямая
функциональная связь. Если
- прямая
функциональная связь. Если 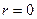 , то значение Х и У в выборке некоррелированы; в случае, если
система случайных величин
, то значение Х и У в выборке некоррелированы; в случае, если
система случайных величин 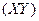 имеет двумерное
нормальное распределение, то величины Х и У будут и независимыми.
имеет двумерное
нормальное распределение, то величины Х и У будут и независимыми.
Если
коэффициент корреляции находится в интервале 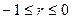 , то между величинами Х и У существует обратная
корреляционная связь. Это находит подтверждение и при визуальном анализе
исходной информации. В этом случае отклонение величины У от среднего значения
взяты с обратным знаком.
, то между величинами Х и У существует обратная
корреляционная связь. Это находит подтверждение и при визуальном анализе
исходной информации. В этом случае отклонение величины У от среднего значения
взяты с обратным знаком.
Если
каждая пара значений величин Х и У чаще всего одновременно оказывается выше
(ниже) соответствующих средних значений, то между величинами существует прямая
корреляционная связь и коэффициент корреляции находится в интервале 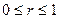 .
.
Если
же отклонение величины Х от среднего значения одинаково часто вызывают
отклонения величины У вниз от среднего значения и при этом отклонения
оказываются все время различными, то можно предполагать, что значение
коэффициента корреляции стремится к нулю.
Следует
отметить, что значение коэффициента корреляции не зависит от единиц измерения и
выбора начала отсчета. Это означает, что если переменные Х и У уменьшить
(увеличить) в К раз либо на одно и то же число С, то коэффициент корреляции не
изменится.
Для упрощения расчетов меры
тесноты корреляционной связи часто применяется индекс корреляционной связи,
который определяется по следующим формулам:
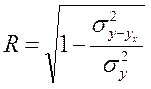 ,
,
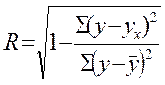 ,
,
где 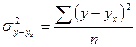 - остаточная дисперсия,
характеризующая вариацию результативного признака под влиянием прочих
неучтенных факторов.
- остаточная дисперсия,
характеризующая вариацию результативного признака под влиянием прочих
неучтенных факторов.
Множественная корреляция
Множественная корреляция –
зависимость результативного и двух или более факторных признаков, включенных в
исследование. Показатель
тесноты связи между результативным и двумя или более факторными признаками
называется множественным или совокупным коэффициентом корреляции и обозначается
R. Совокупный коэффициент предполагает наличие линейной связи
между каждой парой признаков, которая может быть выражена при помощи парных
коэффициентов корреляции. Если находится совокупная мера тесноты связи между
результативным признаком (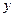 ) и двумя факторными признаками(
) и двумя факторными признаками(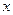 и
и 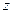 ), то расчет совокупного коэффициента корреляции ведется по
формуле:
), то расчет совокупного коэффициента корреляции ведется по
формуле:
 ,
,
Где подстрочные знаки обозначают, между какими
признаками изучается парная связь.
В формулах расчетов парных коэффициентов
корреляции изменяются лишь символы, обозначающие тот или иной фактор. Так, если
коэффициент корреляции между 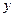 и
и 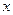 вычисляется по формуле
вычисляется по формуле
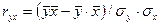 , то коэффициент корреляции между
, то коэффициент корреляции между 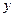 и
и 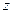 вычисляется:
вычисляется: 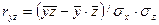 ; между
; между 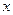 и
и 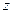 - так:
- так:
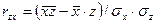
Расчетная часть
Задание 31
1. Имеются следующие данные по десяти
предприятиям за отчетный период:
Таблица 2
|
Предприятия
|
Среднегодовая
стоимость основных
производственных фондов, млн. руб.
|
Выпуск
продукции, млн. руб.
|
|
1
|
15
|
5,0
|
|
2
|
11
|
4,6
|
|
3
|
13
|
6,5
|
|
4
|
14
|
7,0
|
|
5
|
10
|
4,5
|
|
6
|
12
|
5,6
|
|
7
|
8
|
4,0
|
|
8
|
10
|
4,0
|
|
9
|
6
|
2,4
|
|
10
|
9
|
3,6
|
Для изучения связи между
размером среднегодовой стоимости основных производственных фондов и выпуском
продукции вычислите линейное уравнение связи.
2. По приведенным данным: а)
вычислите: линейный коэффициент корреляции; б) проверьте правильность выбора
формы связи, исчислив индекс корреляции.
Решение
1. С помощью табличного
процессора Microsoft Excel построим рабочую таблицу:
Таблица 3
Расчет сумм для
вычисления параметров уравнения прямой
|
№
|
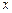
|
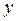
|
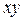
|
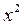
|
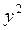
|
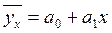 
|
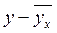
|
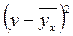
|
|
1
|
15
|
5,0
|
75,0
|
225
|
25,00
|
6,5
|
-1,5
|
2,25
|
|
2
|
11
|
4,6
|
50,6
|
121
|
21,16
|
4,8
|
-0,2
|
0,04
|
|
3
|
13
|
6,5
|
84,5
|
169
|
42,25
|
5,7
|
0,8
|
0,64
|
|
4
|
14
|
7,0
|
98,0
|
196
|
49,00
|
6,1
|
0,9
|
0,81
|
|
5
|
10
|
4,5
|
45,0
|
100
|
20,25
|
4,4
|
0,1
|
0,01
|
|
6
|
12
|
5,6
|
67,2
|
144
|
31,36
|
5,2
|
0,4
|
0,16
|
|
7
|
8
|
4,0
|
32,0
|
64
|
16,00
|
3,5
|
0,5
|
0,25
|
|
8
|
10
|
4,0
|
40,0
|
100
|
16,00
|
4,4
|
-0,4
|
0,16
|
|
9
|
6
|
2,4
|
14,4
|
36
|
5,76
|
2,6
|
-0,2
|
0,04
|
|
10
|
9
|
3,6
|
32,4
|
81
|
12,96
|
3,9
|
-0,3
|
0,09
|
|
Итог
|
108
|
47,2
|
539,1
|
1236
|
239,74
|
47,1
|
0,1
|
4,45
|
Линейное уравнение связи одного фактора записывается в
виде уравнения прямой: 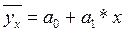

Запишем систему нормальных уравнений:
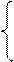
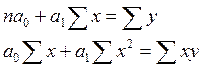
 10*
10*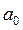 +
+ 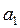 *108 = 47,2 *10,8
*108 = 47,2 *10,8
108*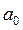 +
+ 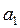 *1236 = 539,1
*1236 = 539,1
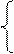 108*
108*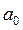 +
+ 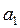 *1166,4 = 509,76
*1166,4 = 509,76
108*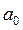 +
+ 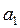 *1236 = 539,1
*1236 = 539,1
-69,6*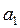 = -29,34
= -29,34
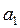 ≈
0,43
≈
0,43
10*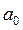 = 47,2 - 108*0,43
= 47,2 - 108*0,43
10*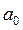 = 0,76
= 0,76
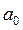 = 0,076
= 0,076
Мы
получили: 
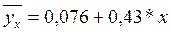
По этому уравнению можно вычислить теоретический
выпуск продукции на одно предприятие (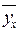 ):
):
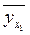 =
0,076 + 0.43*15 = 6,526 ≈ 6,5
=
0,076 + 0.43*15 = 6,526 ≈ 6,5
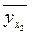 =
0,076 + 0.43*11 = 4,806 ≈ 4,8
=
0,076 + 0.43*11 = 4,806 ≈ 4,8
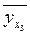 =
0,076 + 0.43*13 = 5,666 ≈ 5,7
=
0,076 + 0.43*13 = 5,666 ≈ 5,7
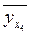 =
0,076 + 0.43*14 = 6,096 ≈ 6,1
=
0,076 + 0.43*14 = 6,096 ≈ 6,1
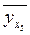 =
0,076 + 0.43*10 = 4,376 ≈ 4,4
=
0,076 + 0.43*10 = 4,376 ≈ 4,4
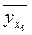 =
0,076 + 0.43*12 = 5,236 ≈ 5,2
=
0,076 + 0.43*12 = 5,236 ≈ 5,2
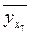 =
0,076 + 0.43*8 = 3,516 ≈ 3,5
=
0,076 + 0.43*8 = 3,516 ≈ 3,5
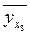 =
0,076 + 0.43*10 = 4,376 ≈ 4,4
=
0,076 + 0.43*10 = 4,376 ≈ 4,4
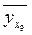 =
0,076 + 0.43*6 = 2656 ≈ 2,6
=
0,076 + 0.43*6 = 2656 ≈ 2,6
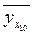 =
0,076 + 0.43*9 = 3,946 ≈ 3,9
=
0,076 + 0.43*9 = 3,946 ≈ 3,9
Отобразим на графике исходные и
вычисленные данные по выпуску продукции:
График с исходными и
полученными в ходе вычислений данными
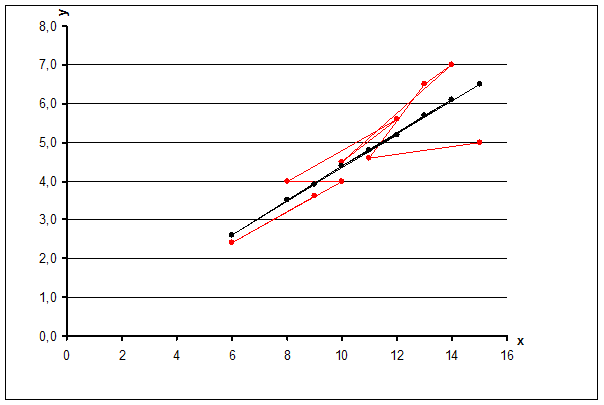
Рис. 1
Вывод:
Видно, что расчетные данные очень хорошо воспроизводят фактические.
Сумма расчетных данных не равна полностью сумме фактических лишь благодаря
округлению расчетов. Найденное линейное уравнение связи 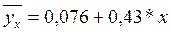 свидетельствует
о том, что увеличение основных фондов предприятия на один миллион рублей
приводит в среднем к увеличению выпуска продукции на 0,43 миллиона рублей.
Параметр
свидетельствует
о том, что увеличение основных фондов предприятия на один миллион рублей
приводит в среднем к увеличению выпуска продукции на 0,43 миллиона рублей.
Параметр 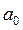 определяет средние условия работы предприятий. Величина
определяет средние условия работы предприятий. Величина
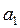 зависит
от принятых единиц измерения обоих признаков.
зависит
от принятых единиц измерения обоих признаков.
2. а) Вычислим линейный коэффициент корреляции:
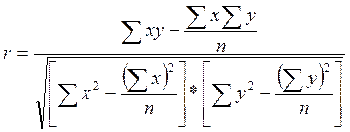
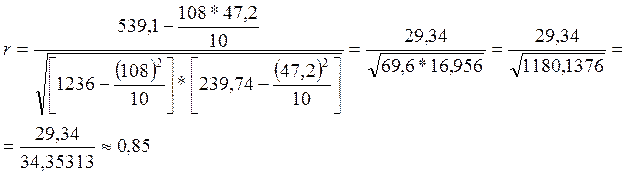
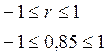
Вывод:
Полученное значение r указывает на тесную корреляционную связь между стоимостью
основных фондов и выпуском продукции. Коэффициент детерминации ((0,85)2)
составляет 0,7225 или 72,25%, что указывает на то, что по приведенным в таблице
данным вариация выпуска продукции на 72,25% обусловлена вариацией основных
фондов и на 27,75% может быть объяснена действием прочих факторов.
б) Проверим правильность
выбора формы связи, исчислив индекс корреляции:
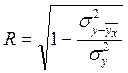 ,
,
где 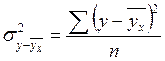 ;
; 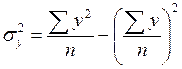
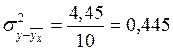
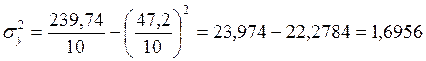
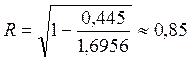
Вывод: Так как r = R = 0,85, то
можно сделать заключение, что гипотеза о линейной форме связи подтверждена.

Аналитическая часть
Задача
В таблице представлены
статистические данные о стоимости основных фондов и выработке одного работника
по десяти предприятиям, производящим одинаковую продукцию:
Таблица 4
[ Источник: www.stat-stayer.narod.ru]
|
Предприятия
|
Стоимость основных фондов,
млн. руб.
|
Выработка одного
работника, тыс. руб.
|
|
1
|
1
|
14
|
|
2
|
2
|
16
|
|
3
|
3
|
15
|
|
4
|
5
|
17
|
|
5
|
7
|
18
|
|
6
|
8
|
21
|
|
7
|
9
|
23
|
|
8
|
10
|
22
|
|
9
|
12
|
24
|
|
10
|
14
|
25
|
По исходным данным найти линейное уравнение связи,
вычислить линейный коэффициент корреляции, теоретическое корреляционное
отношение и индекс корреляции.
Решение
1. С помощью табличного
процессора Microsoft Excel построим рабочую таблицу:
Таблица 5
Расчет сумм для
вычисления параметров уравнения прямой
|
№
|
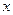
|
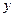
|
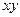
|
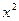
|
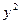
|
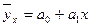
|
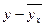
|
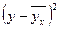
|
|
1
|
1
|
14
|
14
|
1
|
196
|
14,1
|
-0,1
|
0,01
|
|
2
|
2
|
16
|
32
|
4
|
256
|
15,0
|
1,0
|
1,0
|
|
3
|
3
|
15
|
45
|
9
|
225
|
15,8
|
-0,8
|
0,64
|
|
4
|
5
|
17
|
85
|
25
|
289
|
17,6
|
-0,6
|
0,36
|
|
5
|
7
|
18
|
126
|
49
|
324
|
19,4
|
-1,4
|
1,96
|
|
6
|
8
|
21
|
168
|
64
|
441
|
20,3
|
0,7
|
0,49
|
|
7
|
9
|
23
|
207
|
81
|
529
|
21,2
|
1,8
|
3,24
|
|
8
|
10
|
22
|
220
|
100
|
484
|
22,1
|
-0,1
|
0,01
|
|
9
|
12
|
24
|
288
|
144
|
576
|
23,9
|
0,1
|
0,01
|
|
10
|
14
|
25
|
350
|
196
|
625
|
25,6
|
-0,6
|
0,36
|
|
итого
|
71
|
195
|
1535
|
673
|
3945
|
195
|
0
|
8,08
|
Линейное уравнение связи
одного фактора записывается в виде уравнения прямой: 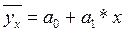

Запишем систему
нормальных уравнений, решение которой и позволяет определить величины
параметров 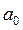 и
и 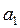 , а следовательно, и уравнение регрессии:
, а следовательно, и уравнение регрессии:
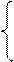
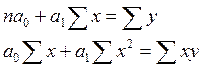
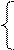 10*
10*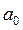 +
+ 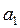 *71 = 195 *7,1
*71 = 195 *7,1
71*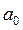 +
+ 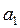 *673 = 1535
*673 = 1535
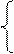 71*
71*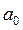 +
+ 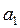 *504,1 = 1384,5
*504,1 = 1384,5
71*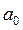 +
+ 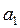 *673 = 1535
*673 = 1535
-168,9*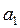 = -150,5
= -150,5
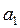 ≈
0,89
≈
0,89
10*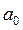 = 195 - 71*0,89
= 195 - 71*0,89
10*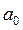 = 131,81
= 131,81
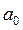 = 13,181
= 13,181
Мы получили: 
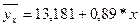
По этому уравнению можно вычислить теоретический
выпуск продукции на одно предприятие (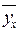 ):
):
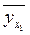 =
13,181 + 0,89*1 = 14,071 ≈ 14,1
=
13,181 + 0,89*1 = 14,071 ≈ 14,1
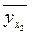 =
13,181 + 0,89*2 = 14,961 ≈ 15,0
=
13,181 + 0,89*2 = 14,961 ≈ 15,0
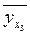 =
13,181 + 0,89*3 = 15,851 ≈ 15,8
=
13,181 + 0,89*3 = 15,851 ≈ 15,8
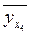 =
13,181 + 0,89*5 = 17,631 ≈ 17,6
=
13,181 + 0,89*5 = 17,631 ≈ 17,6
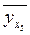 =
13,181 + 0,89*7 = 19,411 ≈ 19,4
=
13,181 + 0,89*7 = 19,411 ≈ 19,4
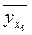 =
13,181 + 0,89*8 = 20,301 ≈ 20,3
=
13,181 + 0,89*8 = 20,301 ≈ 20,3
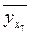 =
13,181 + 0,89*9 = 21,191 ≈ 21,2
=
13,181 + 0,89*9 = 21,191 ≈ 21,2
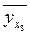 =
13,181 + 0,89*10 = 22,081 ≈ 22,1
=
13,181 + 0,89*10 = 22,081 ≈ 22,1
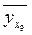 =
13,181 + 0,89*12 = 23,861 ≈ 23,9
=
13,181 + 0,89*12 = 23,861 ≈ 23,9
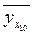 =
13,181 + 0,89*14 = 25,641 ≈ 25,6
=
13,181 + 0,89*14 = 25,641 ≈ 25,6
Отобразим на графике исходные и
вычисленные данные по выпуску продукции:
График с исходными и
полученными в ходе вычислений данными
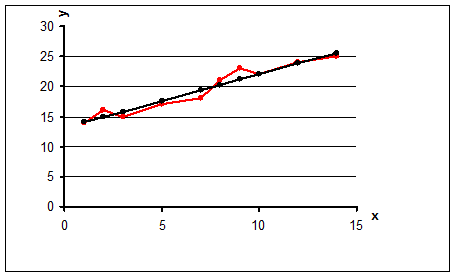
Рис.
2
Вывод:
Видно, что расчетные данные очень хорошо воспроизводят фактические.
Сумма расчетных данных равна сумме фактических. Найденное линейное
уравнение связи 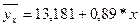 свидетельствует о том, что увеличение основных фондов
предприятия на один миллион рублей приводит в среднем к увеличению выработки
одного работника на 0,89 миллиона рублей. Параметр
свидетельствует о том, что увеличение основных фондов
предприятия на один миллион рублей приводит в среднем к увеличению выработки
одного работника на 0,89 миллиона рублей. Параметр 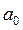 определяет средние условия работы предприятий. Величина
определяет средние условия работы предприятий. Величина
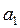 зависит
от принятых единиц измерения обоих признаков.
зависит
от принятых единиц измерения обоих признаков.
2. Вычислим линейный
коэффициент корреляции, теоретическое корреляционное отношение и индекс
корреляции:
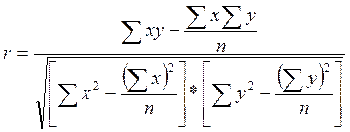
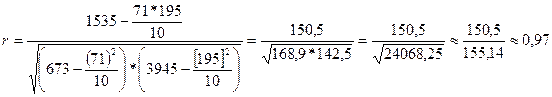
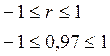
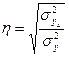 ,
, 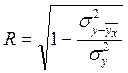 ,
,
где 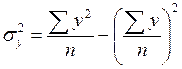 ;
; 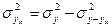 , а
, а 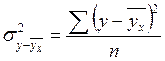
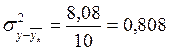
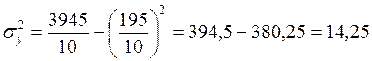
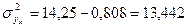
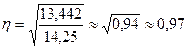
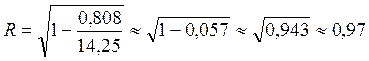
Вывод: Все показатели
тесноты корреляционной связи показывают тесную связь между стоимостью основных фондов и выработкой
одного работника. Коэффициент детерминации ((0,97)2) составляет
0,9409 или 94,09%, что указывает на то, что по приведенным в таблице данным
вариация выработки одного работника на
94,09% обусловлена вариацией основных фондов и на 5,91% может быть объяснена
действием прочих факторов.
Так как r = R = 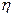 = 0,97, то можно сделать заключение, что гипотеза о
линейной форме связи подтверждена.
= 0,97, то можно сделать заключение, что гипотеза о
линейной форме связи подтверждена.
Заключение
Первая задача изучения
связи методом корреляции состоит в выявлении того, меняется ли в среднем
результативный признак в связи с изменением одного или нескольких факторов. Это
изменение предполагает неизменяемость других факторов, хотя искажающее влияние
этих других факторов на самом деле имеет место. Вторая задача заключается в
определении степени влияния искажающих факторов. Первая задача решается путем
построения уравнений регрессии и носит название регрессионного анализа. Вторая
задача решается путем определения различных показателей тесноты связи и
называется собственно корреляционным анализом.
Теснота связи
количественно выражается величиной коэффициентов корреляции. Коэффициенты
корреляции, представляя количественную характеристику тесноты связи между
признаками, дают возможность определить «полезность» факторных признаков при
построении уравнений множественной регрессии. Величина коэффициентов корреляции
служит также оценкой соответствия уравнению регрессии выявленным
причинно-следственным связям.
Итак, корреляционный и
регрессионный анализ позволяет определить зависимость между факторами, а также
проследить влияние задействованных факторов. Эти показатели имеют широкое
применение в обработке статистических данных для достижения наилучших
показателей в экономических исследованиях.
Список использованной литературы
1.
Адамова
Е.Ф. «Корреляционно-регрессионный анализ в экономических приложениях» - М.:
1998.
2.
Кленин
А.Н., Шевченко К.К. «Математическая статистика для экономистов-статистиков» -
М.: 1990.
3.
Колемаев
В.А., Староверов О.В., Турундаевский В.Б. «Теория вероятностей и математическая
статистика» - М.: 1991.
4.
Одинцов
И.Д. « Теория статистики» - М.: 1999.
5.
«Практикум
по статистике» под редакцией проф. Симчеры В.М. – М.: 1999.
6.
Российский
статистический ежегодник. – М.: 2001.
7.
www.stat-stayer.narod.ru