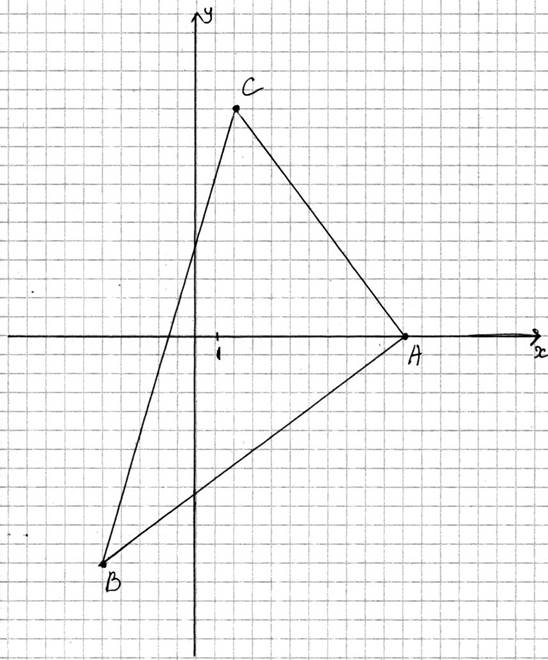
Контрольная работа № 1.
В задачах 1–20 даны координаты вершин треугольника ABC. Сделать чертеж и найти:
1) длины и уравнения сторон треугольника; 2) уравнение высоты AD; 3) уравнение медианы СМ; 4)
уравнение вписанной окружности.
17. A(11;0),
B(–5;–12), C(2;12)
Решение.
1) Длина стороны AB.
|AB|
= 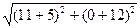 =
= 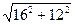 =
= 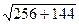 =
= 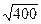 = 20
= 20
Уравнение стороны AB.
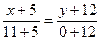
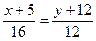
12x+60=16y+192
12x–16y–132=0
3x–4y–33=0
Длина стороны BC.
|BC| = 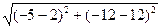 =
= 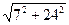 =
= 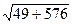 =
= 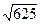 = 25
= 25
Уравнение стороны BC.
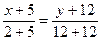
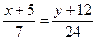
24x+120=7y+84
24x–7y+36=0
Длина стороны AC.
|AC| = 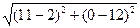 =
= 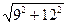 =
= 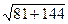 =
= 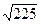 = 15.
= 15.
Уравнение стороны AC.
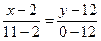
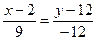
–12x+24=9y–108
12x+9y–132=0
4x+3y–44=0
2) Уравнение высоты AD.
Общее уравнение перпендикуляра к стороне BC.
7x+24y+C1=0
Искомая прямая проходит через точку A.
7∙11+24∙0+C1=0
77+C1=0
C1=–77.
Уравнение высоты AD.
7x+24y–77=0
3) Уравнение медианы CM.
Середина стороны AB – точка M.
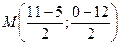
M(3;–6)
Уравнение медианы CM.
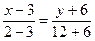
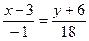
18x–54=–y–6
18x+y–48=0
4) уравнение вписанной окружности.
Центром вписанной окружности треугольника является точка
пересечения биссектрис.
Найдем уравнение биссектрисы угла A.
Для нахождения уравнения биссектрисы AN достаточно найти направляющий вектор
этой прямой в качестве которого можно взять s=AB0+AC0, где AB0 – орт вектора AB, равный 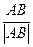 , AC0
– орт вектора AC.
, AC0
– орт вектора AC.
Найдем орты.
AB0
= 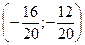
AС0
= 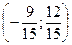
AN =
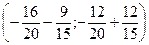 =
= 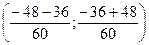 =
= 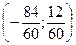 =
= 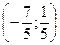
Так как длина направляющего вектора значения не имеет, то
этот вектор можно умножить на любую константу.
(–7;1)
Уравнение биссектрисы AM.

x–11=–7y
x+7y–11=0
Найдем уравнение биссектрисы BP.
Найдем орты.
BC0
= 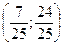
BA0
= 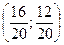
BP =
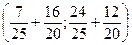 =
= 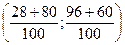 =
= 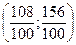 =
= 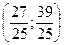
Так как длина направляющего вектора значения не имеет, то
этот вектор можно умножить на любую константу.
(27;39)
(9;13);
Уравнение биссектрисы BP.
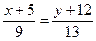
13x+65=9y+108
13x–9y–43=0
Точка пересечения биссектрис.
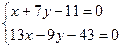
x=–7y+11
–91y+143–9y–43=0
–100y+100=0
y=1
x+7–11=0
x=4
Точка пересечения биссектрис R(4;1), будет центром вписанной
окружности треугольника.
Найдем радиус вписанной окружности треугольника.
Согласно известной формуле
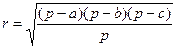 , где p – полупериметр треугольника.
, где p – полупериметр треугольника.
p=(15+20+25)/2=30.
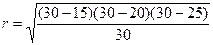 =
= 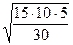 = 5.
= 5.
Получили уравнение вписанной окружности.
(x–4)2+(y–1)2=25
В задачах 21–40 даны координаты вершин пирамиды A1A2A3A4. Найти 1) длину
ребра A1A2; 2) угол между
ребрами A1A2 и A1A4; 3) угол между
ребром А1A4
и гранью A1A2A3; 4) площадь
грани A1A2A3; 5) объем
пирамиды; 6) уравнение прямой A1A2; 7) уравнение
плоскости A1A2A3; 8) уравнение
высоты, опущенной из вершины A4
на грань A1A2A3. Сделать
чертеж.
37. A1(4;4;3),
A2(2;7;3), A3(2;4;9), A4(4;7;1).
Решение.
1) Длина ребра A1A2.
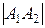 =
= 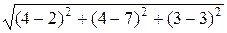 =
= 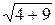 =
= 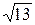 .
.
2) угол между ребрами A1A2
и A1A4.
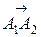 = (2–4;7–4;3–3) = (–2;3;0)
= (2–4;7–4;3–3) = (–2;3;0)
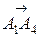 = (4–4;7–4;1–3) = (0;3;–2)
= (4–4;7–4;1–3) = (0;3;–2)
cos φ
=  =
= 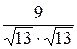 =
= 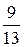 = 0.6923
= 0.6923
φ
= arccos 0.6923 = 0.806
= 46.18°
3) угол между ребром А1A4 и гранью A1A2A3.
Уравнение прямой А1A4.
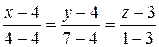
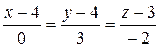
Уравнение плоскости A1A2A3.
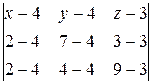 =
= 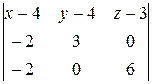 = 18(x–4)–(–12)(y–4)+6(z–3) = 18x–72+12y–48+6z–18 = 18x+12y+6z–138
= 18(x–4)–(–12)(y–4)+6(z–3) = 18x–72+12y–48+6z–18 = 18x+12y+6z–138
Получаем уравнение плоскости
18x+12y+6z–138=0
3x+2y+z–23=0
Угол между прямой и плоскостью
sin φ
= 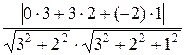 =
= 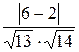 =
= 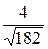 = 0.2965
= 0.2965
φ = arcsin
0.2965 = 0.301 = 17.25°
4) площадь грани A1A2A3.
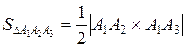
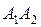 = (–2;3;0)
= (–2;3;0)
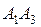 = (2–4;4–4;9–3) = (–2;0;6)
= (2–4;4–4;9–3) = (–2;0;6)
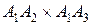 =
= 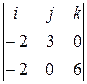 =
= 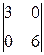 i –
i – 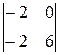 j +
j + 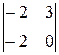 k = 18i + 12j
– 6k
k = 18i + 12j
– 6k
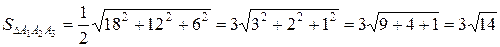
5) Объем пирамиды равен 1/6 объема параллелепипеда,
построенного на векторах A1A2, A1A3 и A1A4;
V = 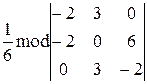 =
= 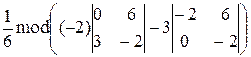 =
= 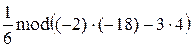 =
= 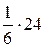 = 4.
= 4.
6) уравнение прямой A1A2.
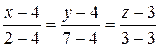
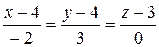
Равенство нулю знаменателя третьей дроби означает, что
прямая лежит в плоскости z=3.
7) уравнение плоскости A1A2A3.
Уравнение этой плоскости было найдено в п. 3).
3x+2y+z–23=0
8) уравнение высоты, опущенной из вершины A4 на грань A1A2A3.
Вектор нормали плоскости A1A2A3 будет
направляющим вектором высоты. Т.к. высота проходит через точку A4, получим ее
уравнение:
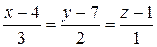
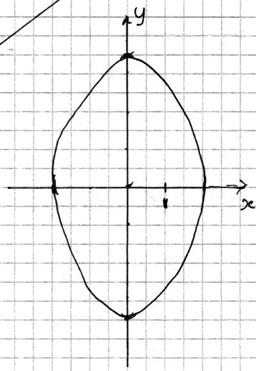
В задачах 50–60 составить уравнение геометрического места
точек, отношение расстояний которых до точки A(x,y) и прямой x=a равно числу b. Сделать чертеж.
57.
A(–1;0); x=–4; b=1/2
Решение.
Расстояние от точки с
координатами (x;y) до точки F с координатами
(–1;0) будет равно 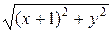
Расстояние от точки с
координатами (x;y) до прямой x=–4 равно x+4.
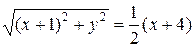
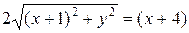
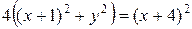
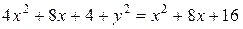
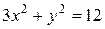
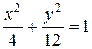
Эллипс.
В задачах 71–80 решить систему линейных уравнений методом
Крамера.
77. 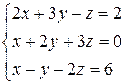
Решение:
∆ = 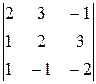 = 2∙
= 2∙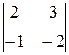 – 3∙
– 3∙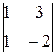 – 1∙
– 1∙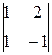 =
2∙(–1)–3∙(–5)–1∙(–3) = –2+ +15+ 3 = 16
=
2∙(–1)–3∙(–5)–1∙(–3) = –2+ +15+ 3 = 16
Т.к. ∆≠0,
то система имеет единственное решение.
∆1 = 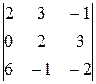 =
= 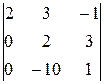 = 2∙
= 2∙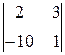 = 2∙32=64
= 2∙32=64
∆2 = 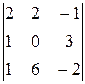 =
= 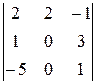 = (–2)∙
= (–2)∙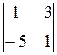 = (–2)∙16 = –32
= (–2)∙16 = –32
∆3 = 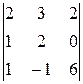 =
= 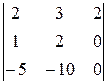 = 0, т.к. вторая и
третья строки пропорциональны.
= 0, т.к. вторая и
третья строки пропорциональны.
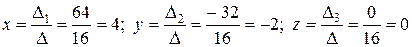
В задачах 81–100 исследовать систему линейных уравнений на
совместность и решить ее, если она совместна.
97. 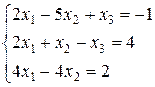
Решение.
Запишем систему в матричной форме.
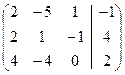 ~
~ 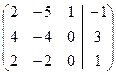 ~
~ 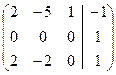 ~
~ 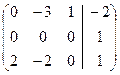
Rg A=2≠3=Rg A*, следовательно система не
совместна.
Контрольная работа № 2.
В задачах 101–120 найти пределы функций, не пользуясь
правилом Лопиталя.
117. а) 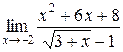 =
= 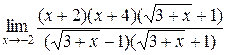 =
= 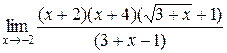 =
= 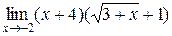 = 2∙2 = 4
= 2∙2 = 4
б) 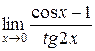 =
= 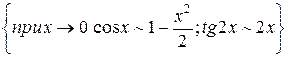 =
= 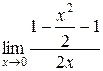 =
= 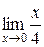 = 0.
= 0.
в) 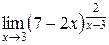 =
= 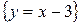 =
=  =
= 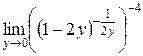 = e–4.
= e–4.
В задачах 121–140 найти производные y’.
137. а) 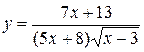
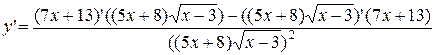 =
= 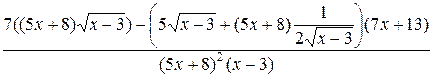 =
= 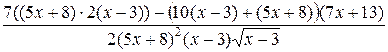 =
= 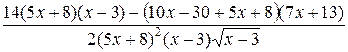 =
= 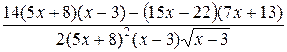 =
= 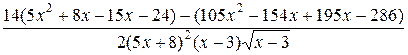 =
= 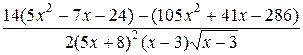 =
= 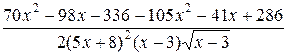 =
= 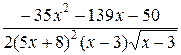
б) 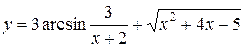
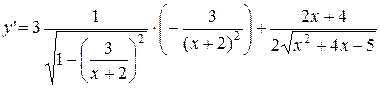 =
= 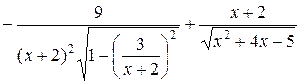 =
= 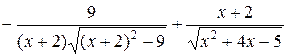 =
= 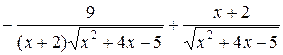 =
= 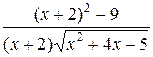 =
= 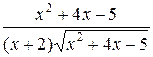 =
= 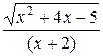
в) 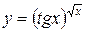
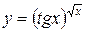 =
= 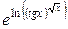 =
= 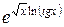
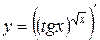 =
= 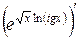 =
= 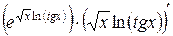 =
= 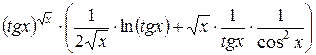 =
= 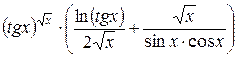
г) 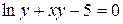
Решение.
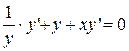
д) 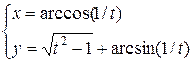
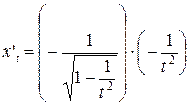 =
= 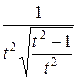 =
= 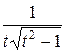
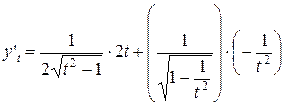 =
= 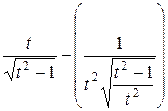 =
= 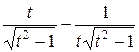 =
= 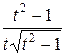 =
= 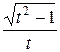
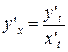 =
= 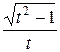 :
: 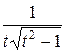 = t2–1.
= t2–1.
В задачах 141–160 найти приближенное значение указанных
величин с помощью дифференциалов соответствующих функций.
157. 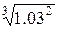
Решение.
Воспользуемся формулой дифференциала.
y(x) ≈ y(x0)+y’(x0)·∆x
В этих обозначениях получим:
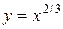
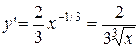
x0=1
x=1.03
∆x=x–x0=0.03
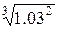 =
= 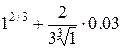 =
= 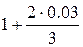 = 1.02
= 1.02
В задачах 161–180 исследовать данные функции методами
дифференциального исчисления и построить их графики. Исследование функции
рекомендуется проводить по следующей схеме: 1) найти область определения
функции; 2) исследовать функцию на непрерывность; 3) определить является ли
данная функция четной, нечетной; 4) найти интервалы возрастания, убывания
функции и ее точки экстремума; 5) найти интервалы выпуклости и вогнутости
графика функции и точки перегиба; 6) найти асимптоты графика функции.
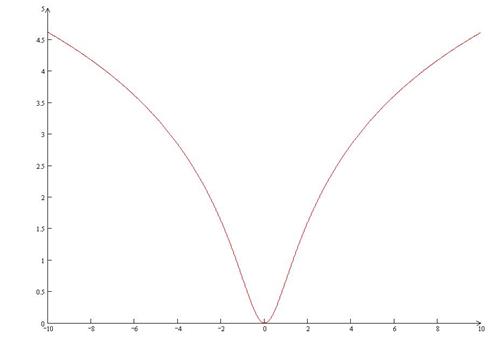
177. y=ln(x2+1)
Решение.
1) Областью определения функции является вся числовая
прямая.
2) Функция является непрерывной в области определения.
3) Четность функции.
y(–x)=ln((–x)2+1)=ln(x2+1)=y(x), т.е. функция четна.
4) Исследуем функцию на монотонность. Для этого найдем
производную.
y’=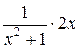 =
= 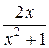
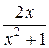 = 0
= 0
x=0
y(0)=0
|
x
|
(–∞;0)
|
0
|
(0;+∞)
|
|
y'
|
–
|
0
|
+
|
|
y
|
↓
|
мин
|
↑
|
5) Исследуем функцию по второй производной.
y"=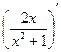 =
= 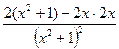 =
= 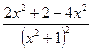 =
= 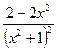
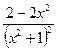 = 0
= 0
2x2=2
x2=1
x=–1;1
y(1)=ln(2)=0.693
y(–1)=ln(2)=0.693
|
x
|
(–∞;–1)
|
–1
|
(–1;1)
|
1
|
(1;+∞)
|
|
y"
|
–
|
0
|
+
|
0
|
–
|
|
y
|
выпукла
|
т.
перегиба
|
вогнута
|
т.
перегиба
|
выпукла
|
6) Асимптоты.
а) т.к. функция непрерывна в области определения, то
вертикальных асимптот нет
б) Невертикальные. y=kx+b
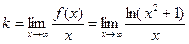 =
= 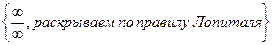 =
= 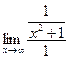 =
= 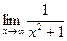 = 0
= 0
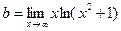 =
= 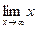 ∙
∙ 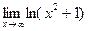 = ∞∙∞ = ∞
= ∞∙∞ = ∞
Асимптот нет.
197. Какой должен быть угол при вершине равнобедренного
треугольника заданной площади, чтобы радиус вписанного в этот треугольник круга
был наибольшим?
Решение.
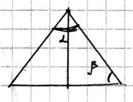
Между элементами любого треугольника имеется соотношение:
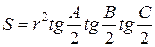
Так как наш треугольник равнобедренный, то это соотношение
можно переписать так:
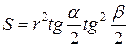 =
= 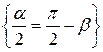 =
= 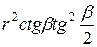 =
= 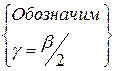 =
= 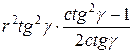 =
= 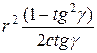 =
= 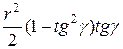 =
= 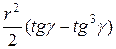
Получили соотношение:
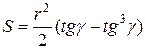
Из него следует, что r достигает минимума тогда, когда
выражение 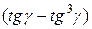 достигает максимума.
достигает максимума.
Найдем производную.
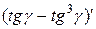 =
= 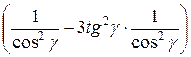 =
= 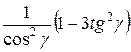
Найдем экстремумы функции.
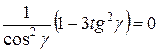
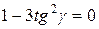
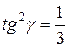
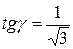
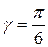
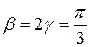
Т.к. 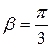 , то искомый треугольник – равносторонний.
, то искомый треугольник – равносторонний.
В задачах 201–220 найти неопределенные интегралы:
217. а) 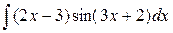 =
= 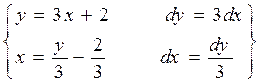 =
= 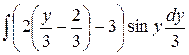 =
= 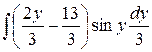 =
= 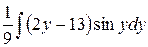 =
= 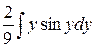 –
– 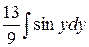 = –
= – 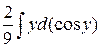 –
– 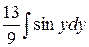 = –
= – 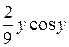 +
+ 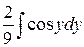 +
+ 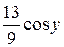 = –
= – 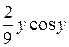 +
+ 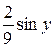 +
+ 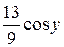 + С = –
+ С = – 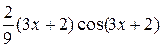 +
+ 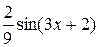 +
+ 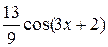 + С =
+ С = 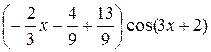 +
+ 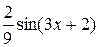 + С =
+ С = 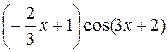 +
+ 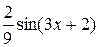 + С
+ С
б) 
Решение.
Разложим подынтегральное выражение на простые дроби.
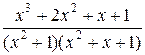 =
= 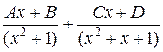 =
= 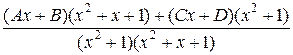 =
= 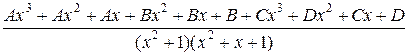
Приравнивая коэффициенты при соответствующих степенях,
получим:
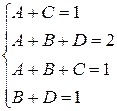
Решив систему, получим:
A=1
C=0
B=0
D=1
Таким образом получаем следующее разложение:
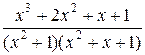 =
= 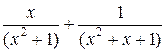
Вернемся к интегралу
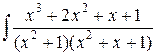 =
= 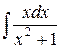 +
+ 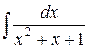
Возьмем полученные интегралы по отдельности.
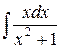 =
= 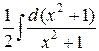 =
= 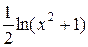 + C
+ C
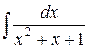 =
= 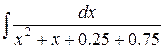 =
= 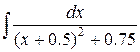 =
= 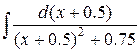 =
= 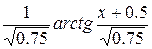 + C =
+ C = 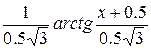 + С =
+ С = 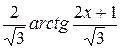 + С
+ С
В итоге получим:
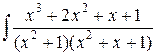 =
= 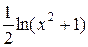 +
+ 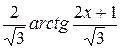 + С
+ С
в) 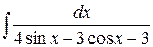 =
= 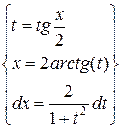 =
= 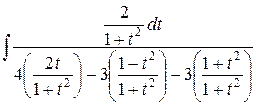 =
= 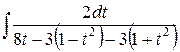 =
= 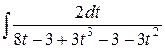 =
= 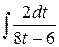 =
= 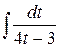 =
= 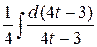 =
= 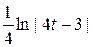 + C =
+ C = 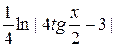 + C
+ C
В задачах 221–240 вычислить несобственный интеграл или
доказать его расходимость:
237. 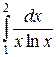 =
= 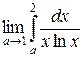 =
= 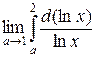 =
= 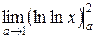 =
= 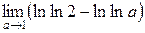 =
= 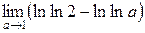 = ln(ln2) – (–∞) = ∞.
= ln(ln2) – (–∞) = ∞.
Следовательно, интеграл расходится.
257. y=x2–2x+1;
y=0; x=2.
Решение.
Объем тела, образованного вращением кривой x=x(y)
вокруг оси Oy равен:
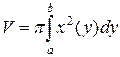
Преобразуем уравнение кривой, в вид x=x(y).
y=x2–2x+1
y=(x–1)2
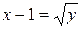
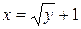
Получаем:
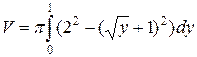 =
= 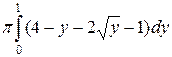 =
= 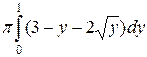 =
= 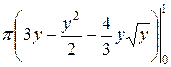 =
= 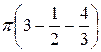 =
= 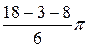 =
= 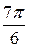 .
.