Задание 1
Имеются следующие
выборочные данные по предприятиям одной
из отраслей промышленности в отчетном году (выборка 20%-ная механическая), млн.
руб.:
Таблица 1
Исходные данные
|
№
органи-зации
п/п
|
Выпуск
про-дукции, млн. руб.
|
Средне-списочная
числен-ность
работ-ников,
чел.
|
Средняя
стоимость основных производ-ственных фондов, млн. руб.
|
№
органи-зации
п/п
|
Выпуск
про-дукции, млн. руб.
|
Средне-списочная
числен-ность
работ-
ников,
чел.
|
Средняя
стоимость основных производ-ственных фондов, млн. руб.
|
|
1
|
36,450
|
162
|
34,714
|
16
|
36,936
|
162
|
34,845
|
|
2
|
23,400
|
156
|
24,375
|
17
|
53,392
|
188
|
46,428
|
|
3
|
46,540
|
179
|
41,554
|
18
|
41,000
|
164
|
38,318
|
|
4
|
59,752
|
194
|
50,212
|
19
|
55,680
|
192
|
47,590
|
|
5
|
41,415
|
165
|
38,347
|
20
|
18,200
|
130
|
19,362
|
|
6
|
26,860
|
158
|
27,408
|
21
|
31,800
|
159
|
31,176
|
|
7
|
79,200
|
220
|
60,923
|
22
|
39,204
|
162
|
36,985
|
|
8
|
54,720
|
190
|
47,172
|
23
|
57,128
|
193
|
48,414
|
|
9
|
40,424
|
163
|
37,957
|
24
|
28,440
|
158
|
28,727
|
|
10
|
30,210
|
159
|
30,210
|
25
|
43,344
|
168
|
39,404
|
|
11
|
42,418
|
167
|
38,562
|
26
|
70,720
|
208
|
55,250
|
|
12
|
64,575
|
205
|
52,500
|
27
|
41,832
|
166
|
38,378
|
|
13
|
51,612
|
187
|
45,674
|
28
|
69,345
|
207
|
55,476
|
|
14
|
35,420
|
161
|
34,388
|
29
|
35,903
|
161
|
34,522
|
|
15
|
14,400
|
120
|
16,000
|
30
|
50,220
|
186
|
44,839
|
Цель статистического исследования - анализ
совокупности организаций по признакам Уровень производительности труда и
Среднегодовая стоимость основных производственных фондов, включая:
·
изучение структуры совокупности по признаку Уровень
производительности труда;
·
выявление наличия корреляционной связи между
признаками Среднегодовая стоимость
основных производственных фондов и Уровень производительности труда
организаций, установление направления связи и оценка её тесноты;
·
применение выборочного метода для определения
статистических характеристик генеральной совокупности организаций.
Задание 1
По исходным данным (табл. 1)
необходимо выполнить следующее:
1.
Построить статистический ряд распределения организаций
по уровню производительности труда, образовав пять
групп с равными интервалами.
2.
Графическим методом и путем расчетов определить
значения моды и медианы полученного ряда распределения.
3.
Рассчитать характеристики ряда распределения: среднюю арифметическую, среднее
квадратическое отклонение, коэффициент вариации.
4.
Вычислить среднюю
арифметическую по исходным данным (табл. 1), сравнить её с аналогичным
показателем, рассчитанным в п. 3 для интервального ряда распределения.
Объяснить причину их расхождения.
Сделать
выводы по результатам выполнения Задания 1.
Выполнение
Задания 1
Целью выполнения
данного Задания
является изучение состава и структуры выборочной совокупности организаций путем
построения и анализа статистического ряда распределения организаций по признаку
Уровень производительности труда.
Таблица 2
|
№
органи-зации
п/п
|
Уровень
производитель-ности
труда,
тыс.руб.
|
Средняя
стоимость основных производст-венных фондов, тыс. руб.
|
№
органи-зации
п/п
|
Уровень производитель-ности труда,
тыс.руб.
|
Средняя
стоимость основных производст-венных фондов, тыс. руб.
|
|
1
|
225
|
34714
|
16
|
228
|
34845
|
|
2
|
150
|
24375
|
17
|
284
|
46428
|
|
3
|
260
|
41554
|
18
|
250
|
38318
|
|
4
|
308
|
50212
|
19
|
290
|
47590
|
|
5
|
251
|
38347
|
20
|
140
|
19362
|
|
6
|
170
|
27408
|
21
|
200
|
31176
|
|
7
|
360
|
60923
|
22
|
242
|
36985
|
|
8
|
288
|
47172
|
23
|
296
|
48414
|
|
9
|
248
|
37957
|
24
|
180
|
28727
|
|
10
|
190
|
30210
|
25
|
258
|
39404
|
|
11
|
254
|
38562
|
26
|
340
|
55250
|
|
12
|
315
|
52500
|
27
|
252
|
38378
|
|
13
|
276
|
45674
|
28
|
335
|
55476
|
|
14
|
220
|
34388
|
29
|
223
|
34522
|
|
15
|
120
|
16000
|
30
|
270
|
44839
|
1. Построение интервального ряда распределения
организаций по уровню производительности труда
Для построения
интервального ряда распределения определяем величину интервала h по формуле:
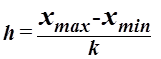 ,
,
где 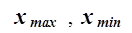 –
наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.
–
наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.
При заданных k = 5,
xmax = 360 и xmin = 120
h = 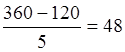 тыс.руб/чел.
тыс.руб/чел.
При
h = 48
границы интервалов ряда распределения имеют следующий вид (табл. 3):
Таблица 3
|
Номер группы
|
Нижняя граница, млн.руб./чел.
|
Верхняя граница, млн.руб./чел.
|
|
1
|
120
|
168
|
|
2
|
168
|
216
|
|
3
|
216
|
264
|
|
4
|
264
|
312
|
|
5
|
312
|
360
|
Определяем
число организаций, входящих в каждую группу, используя принцип полуоткрытого интервала [ ), согласно которому организации со значениями
признаков, которые служат одновременно верхними и нижними границами смежных
интервалов (168, 216, 264 и 312 млн.руб./чел.), будем относить ко второму из
смежных интервалов.
Для определения числа
организаций в каждой группе строим разработочную таблицу 4 (данные графы 4 потребуются при
выполнении Задания 2).
Таблица 4
Разработочная таблица для построения интервального
ряда распределения и аналитической группировки
|
Группы организаций по уровню производитель-ности труда,
тыс.руб.
|
Номер
органи-
зации
|
Уровень производительности труда,
тыс.руб.
|
Средняя стоимость
основных производственных фондов,
тыс.руб.
|
|
1
|
2
|
3
|
4
|
|
120 –168
|
15
|
120
|
16000
|
|
20
|
140
|
19362
|
|
2
|
150
|
24375
|
|
Всего
|
3
|
410
|
59737
|
|
168 –216
|
6
|
170
|
27408
|
|
24
|
180
|
28727
|
|
10
|
190
|
30210
|
|
21
|
200
|
31176
|
|
Всего
|
4
|
740
|
117521
|
|
216 –264
|
14
|
220
|
34388
|
|
29
|
223
|
34522
|
|
1
|
225
|
34714
|
|
16
|
228
|
34845
|
|
22
|
242
|
36985
|
|
9
|
248
|
37957
|
|
18
|
250
|
38318
|
|
5
|
251
|
38347
|
|
27
|
252
|
38378
|
|
11
|
254
|
38562
|
|
25
|
258
|
39404
|
|
3
|
260
|
41554
|
|
Всего
|
12
|
2911
|
447974
|
|
264 - 312
|
30
|
270
|
44839
|
|
13
|
276
|
45674
|
|
17
|
284
|
46428
|
|
8
|
288
|
47172
|
|
19
|
290
|
47590
|
|
23
|
296
|
48414
|
|
4
|
308
|
50212
|
|
Всего
|
7
|
2012
|
330329
|
|
312 – 360
|
12
|
315
|
52500
|
|
28
|
335
|
55476
|
|
26
|
340
|
55250
|
|
7
|
360
|
60923
|
|
Всего
|
4
|
1350
|
224149
|
|
Итого
|
30
|
7423
|
1179710
|
На основе
групповых итоговых строк «Всего» табл. 4 формируем итоговую таблицу 5,
представляющую интервальный ряд распределения фирм по уровню производительности труда.
Таблица 5
Распределение фирм по среднесписочной
численности менеджеров
|
Номер
группы
|
Группы организаций
по уровню производительности труда, тыс.руб.,
x
|
Число фирм,
fj
|
|
1
|
120 – 168
|
3
|
|
2
|
168 – 216
|
4
|
|
3
|
216 – 264
|
12
|
|
4
|
264 - 312
|
7
|
|
5
|
312 – 360
|
4
|
|
ИТОГО
|
30
|
Приведем еще
три характеристики полученного ряда распределения - частоты групп в относительном выражении, накопленные (кумулятивные)
частоты Sj, получаемые путем последовательного суммирования частот всех
предшествующих (j-1) интервалов, и накопленные
частости, рассчитываемые по формуле 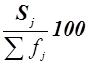 .
.
Таблица 6
Структура организаций по
среднесписочной численности работников
|
Номер
группы
|
Группы организаций
по уровню производитель-ности труда, тыс.руб.,
x
|
Число организаций,
f
|
Накопленная частота
Sj
|
Накопленная
частость, %
|
|
в абсолютном
выражении
|
в % к итогу
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
120 – 168
|
3
|
10
|
3
|
10
|
|
2
|
168 – 216
|
4
|
13
|
7
|
23
|
|
3
|
216 – 264
|
12
|
40
|
19
|
63
|
|
4
|
264 - 312
|
7
|
24
|
26
|
87
|
|
5
|
312 – 360
|
4
|
13
|
30
|
100
|
|
ИТОГО
|
30
|
100
|
|
|
Вывод. Анализ интервального ряда
распределения изучаемой совокупности организаций показывает, что распределение
организаций по уровню производительности труда не является равномерным:
преобладают организации с уровнем производительности труда от 216 до 264
тыс.руб. (это 12 организаций, доля которых составляет 40%); самая малочисленная
группа организаций имеет уровень производительности труда 120 –168 тыс.руб.,
которая включает 3 фирмы, что составляет 10% от общего числа организаций.
2.
Нахождение моды и медианы полученного интервального ряда распределения
графическим методом и путем расчетов
Для определения моды графическим методом строим по данным табл. 6
(графы 2 и 3) гистограмму распределения организаций по изучаемому признаку.
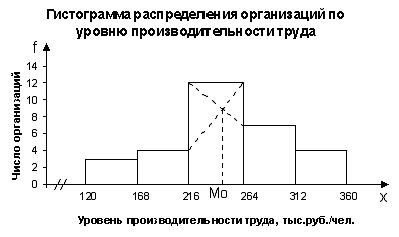
 Рис. 1. Определение моды
графическим методом
Рис. 1. Определение моды
графическим методом
Расчет конкретного значения моды для
интервального ряда распределения производится по формуле:
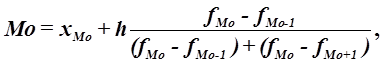
где
хМo – нижняя граница модального
интервала,
h – величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 –
частота интервала, следующего за модальным.
Согласно табл. 4
модальным интервалом построенного ряда является интервал 216 – 264 тыс.руб., т.к. он имеет наибольшую частоту (f3=12). Расчет моды:
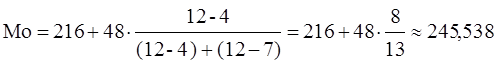 тыс.руб.
тыс.руб.
Вывод. Для рассматриваемой совокупности
организаций наиболее распространенный уровень производительности труда
характеризуется средней величиной
245,538 тыс. руб.
Для определения медианы графическим методом строим по данным табл.
6 (графы 2 и 5) кумуляту распределения организаций по изучаемому признаку.
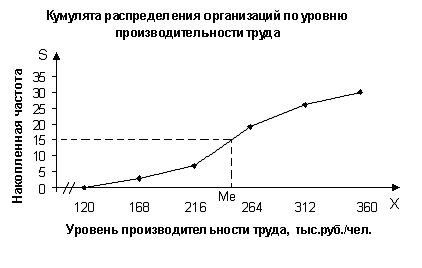
Рис. 2. Определение медианы
графическим методом
Расчет конкретного значения медианы для интервального ряда
распределения производится по формуле
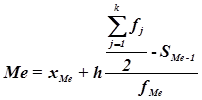 ,
,
где
хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
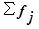 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота
интервала, предшествующего медианному.
Определяем медианный
интервал, используя графу 5 табл. 6. Медианным интервалом является интервал 216 –264 тыс.руб., т.к. именно в этом интервале
накопленная частота Sj=19 впервые превышает
полусумму всех частот (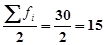 ).
).
Расчет медианы:
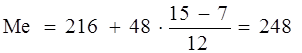 тыс. руб.
тыс. руб.
Вывод. В рассматриваемой совокупности
организаций половина организаций имеют уровень производительности труда не
более 248 тыс.руб., а другая половина – не менее 248 тыс.руб.
3. Расчет
характеристик ряда распределения
Для расчета характеристик ряда распределения 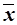 , σ, σ2, Vσ на основе табл. 6 строим
вспомогательную таблицу 6 (
, σ, σ2, Vσ на основе табл. 6 строим
вспомогательную таблицу 6 (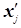 – середина интервала).
– середина интервала).
Таблица 7
Расчетная таблица для
нахождения характеристик ряда распределения
|
Группы организаций
по уровню производитель-ности труда, тыс.руб.,
X
|
Середина интервала,
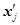
|
Число органи-заций,
fj
|
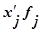
|

|
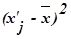
|
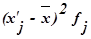
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
120 – 168
|
144
|
3
|
432
|
-104
|
10816
|
32448
|
|
168 – 216
|
192
|
4
|
768
|
-56
|
3136
|
12544
|
|
216 – 264
|
240
|
12
|
2880
|
-8
|
64
|
768
|
|
264 - 312
|
288
|
7
|
2016
|
40
|
1600
|
11200
|
|
312 – 360
|
336
|
4
|
1344
|
88
|
7744
|
30976
|
|
ИТОГО
|
|
30
|
7440
|
|
|
87936
|
Рассчитаем среднюю арифметическую
взвешенную:
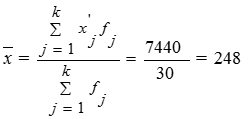 тыс.руб.
тыс.руб.
Рассчитаем среднее квадратическое
отклонение:
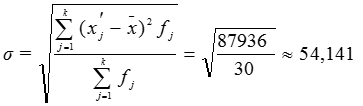 тыс.руб.
тыс.руб.
Рассчитаем дисперсию:
σ2 = 54,1412 = 2931,2
Рассчитаем коэффициент вариации:
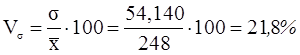
Вывод. Анализ полученных значений
показателей 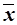 и σ говорит о том, что
средняя величина уровня производительности труда составляет 248 тыс.руб.,
отклонение от этой величины в ту или иную сторону составляет в среднем 54,141
тыс.руб. (или 21,8%), наиболее характерная среднесписочная численность
работников находится в пределах от 193,859 до 302,141 тыс.руб. (диапазон
и σ говорит о том, что
средняя величина уровня производительности труда составляет 248 тыс.руб.,
отклонение от этой величины в ту или иную сторону составляет в среднем 54,141
тыс.руб. (или 21,8%), наиболее характерная среднесписочная численность
работников находится в пределах от 193,859 до 302,141 тыс.руб. (диапазон 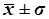 ).
).
Значение Vσ = 21,8% не превышает 33%,
следовательно, вариация уровня производительности труда в исследуемой
совокупности организаций незначительна и совокупность по данному признаку
однородна. Расхождение между значениями 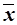 , Мо и Ме незначительно (
, Мо и Ме незначительно (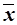 =248 тыс.руб., Мо=245,538
тыс.руб., Ме=248 тыс.руб.), что
подтверждает вывод об однородности совокупности организаций. Таким образом,
найденное среднее значение уровня производительности труда (248 тыс.руб.)
является типичной, надежной характеристикой исследуемой совокупности
организаций.
=248 тыс.руб., Мо=245,538
тыс.руб., Ме=248 тыс.руб.), что
подтверждает вывод об однородности совокупности организаций. Таким образом,
найденное среднее значение уровня производительности труда (248 тыс.руб.)
является типичной, надежной характеристикой исследуемой совокупности
организаций.
4. Вычисление средней арифметической по
исходным данным об уровне
производительности труда
Для расчета применяется формула средней арифметической
простой:
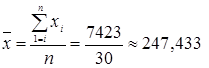 тыс.руб.
тыс.руб.
Причина расхождения
средних величин, рассчитанных по исходным данным (247,433 тыс.руб.) и по
интервальному ряду распределения (248 чел.), заключается в том, что в первом
случае средняя определяется по фактическим значениям исследуемого
признака для всех 30-ти организаций, а во втором случае в качестве значений
признака берутся середины интервалов 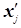 и, следовательно, значение средней будет менее
точным.
и, следовательно, значение средней будет менее
точным.
Задание 2
По исходным
данным (табл. 1) с использованием
результатов выполнения Задания 1 необходимо выполнить следующее:
1.
Установить наличие и характер корреляционной связи
между признаками Среднегодовая стоимость основных производственных фондов и
Уровень производительности труда, образовав пять групп с равными
интервалами по каждому из признаков, используя методы:
а) аналитической
группировки;
б) корреляционной
таблицы.
2. Измерить
тесноту корреляционной связи, используя коэффициент
детерминации и эмпирическое корреляционное отношение.
Сделать
выводы по результатам выполнения задания 2.
Выполнение задания 2
Целью
выполнения данного задания
является выявление наличия корреляционной связи между факторным и
результативным признаками, а также установление направления связи и оценка ее
тесноты.
По условию
Задания 2 факторным является признак Уровень производительности труда,
результативным – признак Среднегодовая стоимость основных производственных
фондов.
1.
Установление наличия и характера корреляционной связи между признаками Уровень
производительности труда и Среднегодовая стоимость основных производственных фондов методами
аналитической группировки и корреляционных таблиц
1а. Применение метода аналитической группировки
Аналитическая группировка строится
по факторному признаку Х и для
каждой j-ой группы ряда
определяется среднегрупповое значение 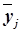 результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения
результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения 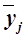 систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
Используя разработочную таблицу 4, строим аналитическую группировку,
характеризующую зависимость между факторным признаком Х- Уровень
производительности труда и результативным признаком Y - Среднегодовая
стоимость основных производственных фондов. Макет аналитической
таблицы имеет следующий вид (табл. 8):
Таблица 8
Зависимость среднегодовой
стоимости основных производственных фондов
от уровня производительности труда
|
Номер группы
|
Группы организаций
по уровню производительности труда, тыс.руб.,
X
|
Число организаций,
fj
|
Уровень
производительности труда, тыс. руб.
|
|
всего
|
в среднем на одну
организацию,
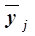
|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИТОГО
|
|
|
|
Групповые средние значения 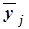 получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 9:
получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 9:
Таблица 9
Зависимость объема продаж от
среднесписочной численности менеджеров
|
Номер группы
|
Группы организаций
по уровню производительности труда, млн.руб.,
x
|
Число фирм,
fj
|
Средняя стоимость основных производственных
фондов, млн. руб.
|
|
всего
|
в среднем на одну
организацию,
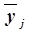
|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
1
|
0,120 – 0,168
|
3
|
59,737
|
19,9123
|
|
2
|
0,168 – 0,216
|
4
|
117,521
|
29,3803
|
|
3
|
0,216 – 0,264
|
12
|
447,974
|
37,3312
|
|
4
|
0,264 – 0,312
|
7
|
330,329
|
47,1899
|
|
5
|
0,312 – 0,360
|
4
|
224,149
|
56,0373
|
|
|
ИТОГО
|
30
|
1179,710
|
|
Вывод. Анализ данных табл. 9 показывает, что с увеличением
уровня производительности труда от группы к группе систематически возрастает и
среднегодовая стоимость основных производственных фондов по каждой группе
организаций, что свидетельствует о наличии прямой корреляционной связи между
исследуемыми признаками.
1б.
Применение метода корреляционных таблиц
Корреляционная
таблица строится как комбинация двух рядов распределения по факторному признаку
Х и результативному признаку Y. На
пересечении j-ой строки
и k-ой графы
таблицы указывается число единиц совокупности, входящих в j-ый интервал по признаку X и в k-ый
интервал по признаку Y.
Концентрация частот около диагонали построенной таблицы свидетельствует о наличии
корреляционной связи между признаками - прямой или обратной. Связь прямая, если
частоты располагаются по диагонали, идущей от левого верхнего угла к правому
нижнему, обратная - по диагонали от правого верхнего угла к левому нижнему.
Для
построения корреляционной таблицы необходимо знать величины и границы
интервалов по двум признакам X и Y. Для
факторного признака Х – Уровень производительности труда эти величины известны из
табл. 4 Определяем величину интервала для результативного признака Y – Среднегодовая стоимость основных производственных фондов при k = 5, уmax = 60,923млн. руб., уmin = 16,000млн. руб.:
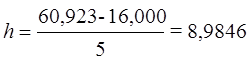 млн.руб.
млн.руб.
Границы интервалов ряда распределения
результативного признака Y имеют вид:
Таблица 10
|
Номер группы
|
Нижняя граница,
млн. руб.
|
Верхняя граница,
млн. руб.
|
|
1
|
16,0000
|
24,9846
|
|
2
|
24,9846
|
33,9692
|
|
3
|
33,9692
|
42,9538
|
|
4
|
42,9538
|
51,9384
|
|
5
|
51,9384
|
60,9230
|
Подсчитывая для каждой группы число входящих в нее
организаций с использованием принципа полуоткрытого интервала [ ),
получаем интервальный ряд распределения результативного признака (табл. 11).
Таблица 11
Интервальный ряд распределения организаций по среднегодовой стоимости
основных производственных фондов
|
Группы организаций по среднегодовой
стоимости основных производственных фондов млн. руб.,
У
|
Число организаций,
fj
|
|
16,000-24,9846
|
3
|
|
24,9846-33,9692
|
4
|
|
33,9692-42,9538
|
12
|
|
42,9538-51,9384
|
7
|
|
51,9384-60,9230
|
4
|
|
ИТОГО
|
30
|
Используя группировки по факторному и результативному
признакам, строим корреляционную таблицу (табл. 12).
Таблица
12
Корреляционная таблица зависимости среднегодовой стоимости основных
производственных фондов
от уровня производительности
труда
|
Группы организаций
по уровню производительности труда, млн.руб.,
|
Группы организаций по среднегодовой
стоимости основных производственных фондов млн. руб.,
|
ИТОГО
|
|
16,000-24,9846
|
24,9846-33,9692
|
33,9692-42,9538
|
42,9538-51,9384
|
51,9384-60,9230
|
|
0,120 – 0,168
|
3
|
|
|
|
|
3
|
|
0,168 – 0,216
|
|
4
|
|
|
|
4
|
|
0,216 – 0,264
|
|
|
12
|
|
|
12
|
|
0,264 – 0,312
|
|
|
|
7
|
|
7
|
|
0,312 – 0,360
|
|
|
|
|
4
|
4
|
|
ИТОГО
|
3
|
4
|
12
|
7
|
4
|
30
|
Вывод. Анализ
данных табл. 12 показывает, что распределение частот групп произошло вдоль
диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это
свидетельствует о наличии прямой корреляционной связи между уровнем
производительности труда и среднегодовой стоимостью основных производственных
фондов.
2. Измерение тесноты корреляционной связи с использованием коэффициента
детерминации 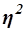 и эмпирического корреляционного отношения
и эмпирического корреляционного отношения 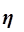
Коэффициент детерминации 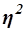 характеризует
силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля
межгрупповой дисперсии
характеризует
силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля
межгрупповой дисперсии 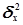 признака Y в его
общей дисперсии
признака Y в его
общей дисперсии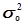 :
:
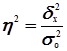
где 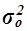 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Общая
дисперсия 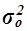 характеризует
вариацию результативного признака, сложившуюся под влиянием всех
действующих на Y факторов (систематических
и случайных) и вычисляется по формуле
характеризует
вариацию результативного признака, сложившуюся под влиянием всех
действующих на Y факторов (систематических
и случайных) и вычисляется по формуле
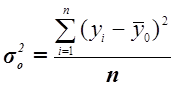 ,
(10)
,
(10)
где yi – индивидуальные значения
результативного признака;
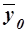 – общая средняя значений
результативного признака;
– общая средняя значений
результативного признака;
n – число единиц совокупности.
Межгрупповая дисперсия  измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
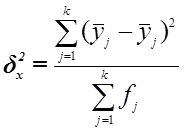 ,
(13)
,
(13)
где 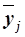 –групповые
средние,
–групповые
средние,
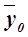 –
общая средняя,
–
общая средняя,
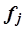 –число единиц в j-ой
группе,
–число единиц в j-ой
группе,
k – число групп.
Для расчета показателей 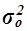 и
и  необходимо знать
величину общей средней
необходимо знать
величину общей средней 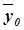 , которая
вычисляется как средняя арифметическая простая по всем единицам совокупности:
, которая
вычисляется как средняя арифметическая простая по всем единицам совокупности:
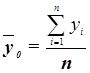
Значения числителя и знаменателя формулы имеются
в табл. 8 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую
среднюю 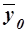 :
:
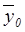 =
=
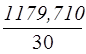 =39,3237 млн.руб.
=39,3237 млн.руб.
Для
расчета общей дисперсии 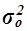 применяется вспомогательная таблица
13.
применяется вспомогательная таблица
13.
Таблица 13
Вспомогательная таблица для расчета общей дисперсии
|
Номер
фирмы
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
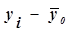
|
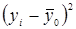
|
|
1
|
2
|
3
|
4
|
|
1
|
34,714
|
-4,610
|
21,2493
|
|
2
|
24,375
|
-14,949
|
223,4636
|
|
3
|
41,554
|
2,230
|
4,9742
|
|
4
|
50,212
|
10,888
|
118,5551
|
|
5
|
38,347
|
-0,977
|
0,9539
|
|
6
|
27,408
|
-11,916
|
141,9839
|
|
7
|
60,923
|
21,599
|
466,5298
|
|
8
|
47,172
|
7,848
|
61,5958
|
|
9
|
37,957
|
-1,367
|
1,8679
|
|
10
|
30,210
|
-9,114
|
83,0595
|
|
11
|
38,562
|
-0,762
|
0,5802
|
|
12
|
52,500
|
13,176
|
173,6149
|
|
13
|
45,674
|
6,350
|
40,3263
|
|
14
|
34,388
|
-4,936
|
24,3611
|
|
15
|
16,000
|
-23,324
|
543,9950
|
|
16
|
34,845
|
-4,479
|
20,0588
|
|
17
|
46,428
|
7,104
|
50,4711
|
|
18
|
38,318
|
-1,006
|
1,0114
|
|
19
|
47,590
|
8,266
|
68,3317
|
|
20
|
19,362
|
-19,962
|
398,4695
|
|
21
|
31,176
|
-8,148
|
66,3850
|
|
22
|
36,985
|
-2,339
|
5,4695
|
|
23
|
48,414
|
9,090
|
82,6336
|
|
24
|
28,727
|
-10,597
|
112,2901
|
|
25
|
39,404
|
0,080
|
0,0064
|
|
26
|
55,250
|
15,926
|
253,6470
|
|
27
|
38,378
|
-0,946
|
0,8943
|
|
28
|
55,476
|
16,152
|
260,8968
|
|
29
|
34,522
|
-4,802
|
23,0563
|
|
30
|
44,839
|
5,515
|
30,4185
|
|
Итого
|
1179,710
|
|
3281,1507
|
Рассчитаем общую
дисперсию:
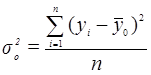 =
=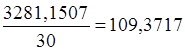
Для расчета межгрупповой дисперсии  строится вспомогательная таблица 14 При этом используются групповые средние значения
строится вспомогательная таблица 14 При этом используются групповые средние значения 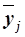 из табл. 9 (графа 5).
из табл. 9 (графа 5).
Таблица 14
Вспомогательная таблица для расчета межгрупповой дисперсии
|
Группы организаций
по уровню производительности труда, млн.руб.,
x
|
Число
органи-заций,
fj
|
Среднее значение в
группе, млн. руб.
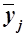
|
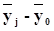
|
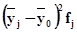
|
|
1
|
2
|
3
|
4
|
5
|
|
0,120 – 0,168
|
3
|
19,9123
|
-19,4114
|
1130,4073
|
|
0,168 – 0,216
|
4
|
29,3803
|
-9,9434
|
395,4848
|
|
0,216 – 0,264
|
12
|
37,3312
|
-1,9925
|
47,6407
|
|
0,264 – 0,312
|
7
|
47,1899
|
7,8662
|
433,1397
|
|
0,312 – 0,360
|
4
|
56,0373
|
16,7136
|
1117,3777
|
|
ИТОГО
|
30
|
|
|
3124,0503
|
Рассчитаем межгрупповую дисперсию:
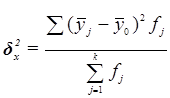
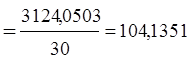
Определяем
коэффициент детерминации:
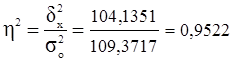 или
95,2%
или
95,2%
Эмпирическое корреляционное отношение 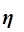 оценивает тесноту
связи между факторным и результативным признаками и вычисляется по
формуле
оценивает тесноту
связи между факторным и результативным признаками и вычисляется по
формуле
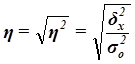
Рассчитаем
показатель 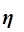 :
:
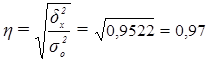
Вывод: согласно
шкале Чэддока связь между уровнем производительности труда и среднегодовой
стоимостью основных производственных фондов организаций является весьма тесной.
Задание 3
По
результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:
1)ошибку выборки среднего уровня производительности труда, и границы, в которых будет находиться
производительность труда в генеральной совокупности.
2)ошибку выборки доли
организаций с уровнем производительности труда 264 тыс.руб. и более и границы,
в которых будет находиться генеральная доля.
Выполнение Задания 3
Целью выполнения
данного Задания
является определение для генеральной совокупности организаций региона границ, в
которых будут находиться средняя величина уровня
производительности труда,
и доля организаций с уровнем производительности
труда не менее
264 тыс.руб.
1.
Определение ошибки выборки для величины
среднесписочной численности менеджеров, а также границ, в которых будет
находиться генеральная средняя
Применяя
выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки
репрезентативности), т.к. генеральные и выборочные характеристики, как правило,
не совпадают, а отклоняются на некоторую величину ε.
Принято вычислять два вида
ошибок выборки - среднюю 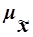 и предельную
и предельную 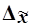 .
.
Для расчета средней ошибки выборки 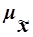 применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
Для собственно-случайной
и механической выборки с бесповторным способом отбора средняя ошибка 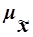 для выборочной средней
для выборочной средней 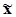 определяется по
формуле
определяется по
формуле
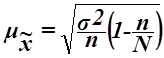 ,
,
где 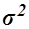 – общая дисперсия изучаемого признака,
– общая дисперсия изучаемого признака,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной совокупности.
Предельная ошибка выборки 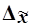 определяет границы, в пределах
которых будет находиться генеральная средняя:
определяет границы, в пределах
которых будет находиться генеральная средняя:
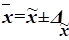 ,
,
 ,
,
где 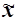 – выборочная средняя,
– выборочная средняя,
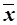 – генеральная средняя.
– генеральная средняя.
Предельная
ошибка выборки 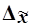 кратна средней ошибке
кратна средней ошибке 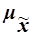 с коэффициентом кратности t (называемым также коэффициентом доверия):
с коэффициентом кратности t (называемым также коэффициентом доверия):
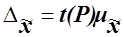
Коэффициент
кратности t зависит от
значения доверительной вероятности
Р, гарантирующей вхождение генеральной средней в интервал 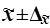 , называемый доверительным интервалом.
, называемый доверительным интервалом.
Наиболее
часто используемые доверительные вероятности Р и соответствующие им
значения t задаются следующим образом (табл. 15):
Таблица 15
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию Задания 2 выборочная совокупность насчитывает 30
фирм, выборка 20% механическая, следовательно, генеральная совокупность включает
150 фирм. Выборочная средняя 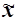 , дисперсия
, дисперсия 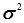 определены
в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 16:
определены
в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 16:
Таблица 16
|
Р
|
t
|
n
|
N
|
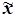
|
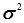
|
|
0,954
|
2
|
30
|
150
|
248
|
2931,2
|
Рассчитаем среднюю ошибку выборки:
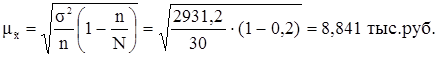
Рассчитаем
предельную ошибку выборки:
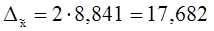 тыс.руб.
тыс.руб.
Определим
доверительный интервал для генеральной средней:
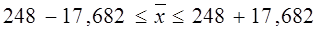
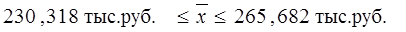
Вывод. На основании проведенного
выборочного обследования с вероятностью 0,954 можно утверждать, что для
генеральной совокупности организаций средняя величина уровня производительности
труда находится в пределах от 230,318 до 265,682 тыс.руб.
2. Определение
ошибки выборки для доли организаций с уровнем производительности труда 264
тыс.руб и более и границы, в которых будет находиться генеральная доля
Доля
единиц выборочной совокупности, обладающих тем или иным заданным свойством,
выражается формулой
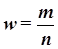 ,
,
где m – число
единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для собственно-случайной
и механической выборки с бесповторным способом отбора предельная
ошибка выборки 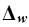 доли единиц,
обладающих заданным свойством, рассчитывается по формуле
доли единиц,
обладающих заданным свойством, рассчитывается по формуле
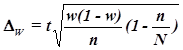 ,
,
где
w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не обладающих заданным свойством,
N – число единиц в генеральной
совокупности,
n– число единиц в выборочной
совокупности.
Предельная ошибка выборки 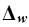 определяет границы, в пределах
которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
определяет границы, в пределах
которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
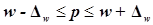
По
условию Задания 3 исследуемым свойством фирм является равенство или превышение уровня
производительности труда величины 264 тыс.руб.
Число
организаций с данным свойством определяется из табл. 4 (графа 3):
m=11
Рассчитаем
выборочную долю:
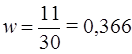
Рассчитаем
предельную ошибку выборки для доли:
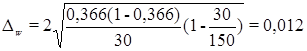
Определим
доверительный интервал генеральной доли:
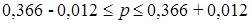
0,354 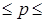 0,378
0,378
или
35,4% 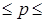 37,8%
37,8%
Вывод. С вероятностью
0,954 можно утверждать, что в генеральной совокупности организаций региона доля
организаций с уровнем производительности труда 264 тыс.руб. и более будет находиться в
пределах от 35,4% до 37,8%.