Задание 1.

Задача 1.1. На кондитерской фабрике.

            Маленькая кондитерская фабрика должна закрыться на реконструкцию, поэтому надо реализовывать оставшиеся запасы сырья, получив максимальную прибыль. Запасы и расход сырья для производства единицы продукции каждого вида, а также получаемая при этом прибыль представлены в таблице.

Ресурсы	Кондитерские изделия	Ограничения
Ореховый звон	Райский вкус	Батончик	Белка	Ромашка
Темный шоколад	0,8	0,5	1	2	1,1	1411
Светлый шоколад	0,2	0,1	0,1	0,1	0,2	149
Сахар	0,3	0,4	0,6	1,3	0,05	815,5
Карамель	0,2	0,3	0,3	0,7	0,5	466
Орехи	0,7	0,1	0,9	1,5	0	1080
Прибыль	1	0,7	1,1	2	0,6

1. Мастер, используя свой 20-летний опыт, предлагает «на глазок» выпустить по 200 пакетиков каждого продукта, утверждая, что ресурсов «должно хватить», а прибыль получится 1080 у.е. Сын владельца фабрики, только что прошедший курсы по математическому моделированию, утверждает, что такие проблемы надо решать с помощью линейного программирования. Отец обещает сыну всю прибыль сверх 1080 у.е., если он предложит лучший план, чем опытный мастер.

Требуется:

1)      определить оптимальный план выпуска продукции. Какую прибыль планирует получить сын?

2)      проанализировать использование ресурсов в оптимальном плане.

1.      Экономико-математическая модель задачи.

 

Обозначим через x₁, x₂, x₃, x₄, x₅ – количество производства кондитерских изделий.

Целевая функция – это выражение, которое необходимо максимизировать:

                                   f(x) = x₁ + 0,7x₂ + 1,1x₃ + 2x₄ + 0,6x₅ → max

Ограничения задачи имеет вид:

                                   0,8x₁ + 0,5x₂ +      x₃ +    2x₄ +  1,1x₅ £ 1411

                                   0,2x₁ + 0,1x₂ + 0,1x₃ + 0,1x₄ +  0,2x₅ £ 149

                                   0,3x₁ + 0,4x₂ + 0,6x₃ + 1,3x₄ + 0,05x₅ £ 815,5

                                   0,2x₁ + 0,3x₂ + 0,3x₃ + 0,7x₄ +   0,5x₅ £ 466

                                   0,7x₁ + 0,1x₂ + 0,9x₃ + 1,5x₄                £ 1080

                                   x₁, x₂, x₃, x₄, x₅ ≥ 0

     

2.      Поиск оптимального плана выпуска.

 

Решение задачи выполним с помощью надстройки Excel Поиск решения.

Оптимальные значения вектора X = (X₁, X₂, X₃, X₄, X₅), будут помещены в ячейках B3:F3, а оптимальное значение целевой функции – в ячейке G4.

           

Введем исходные данные. Сначала опишем целевую функцию с помощью функции – СУММАПРОИЗВ, а потом введем данные для левых частей ограничений.

Исходный рабочий лист Excel.

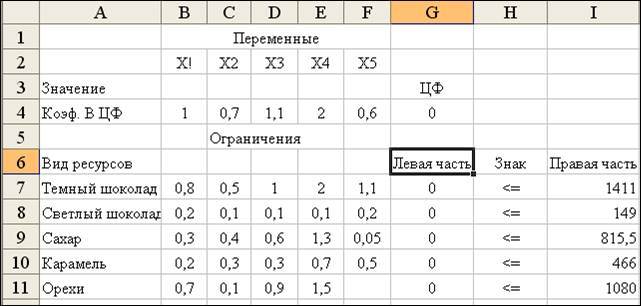
В Поиске решения введем направление целевой функции, адреса искомых переменных, добавим ограничения. Надо учитывать, что пакетиков может быть только целое количество, т.е. x₁, x₂, x₃, x₄, x₅ могут принимать только целые значения. На экране появится диалоговое окно Поиска решения с введенными условиями.

Диалоговое окно Поиск решения.

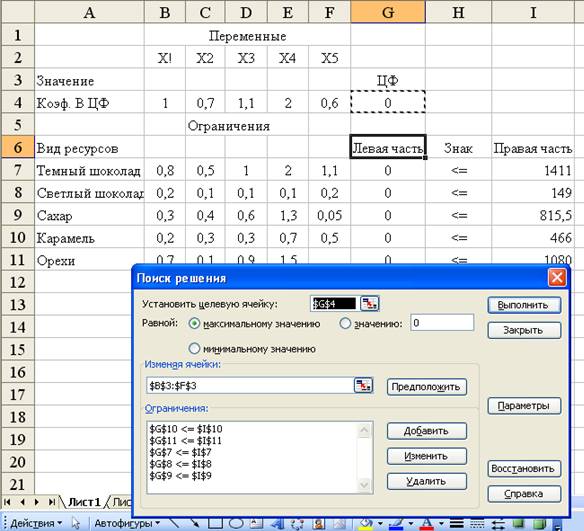
            В Параметрах поиска решения установим флажки в окнах Линейная модель и Неотрицательные значения.

Диалоговое окно Параметры поиска решения.

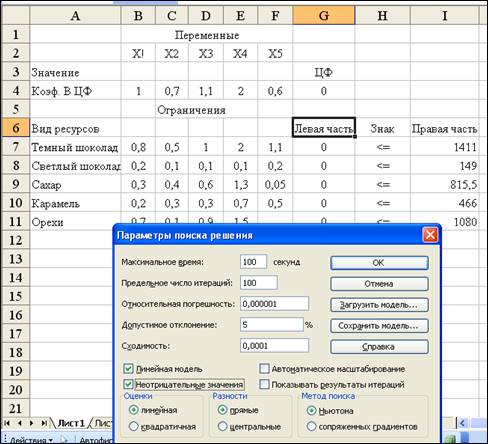
            После ввода параметров для решения следует нажать кнопку Выполнить. На экране появится сообщение, что решение найдено.

Диалоговое окно Результаты поиска решения.

 

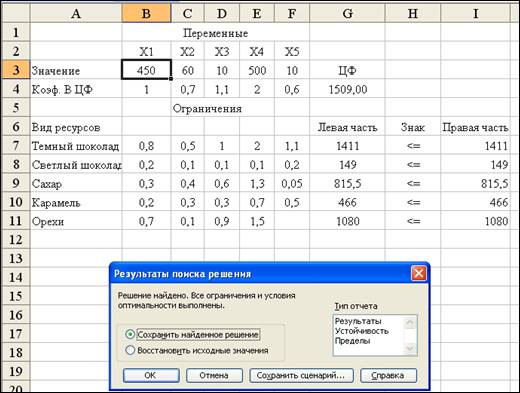
            Полученное решение означает, что максимальный доход 1509 у.е. фабрика может получить при выпуске 450 пакетиков орехового звона, 60 пакетиков райского вкуса, 10 батончиков, 500 пакетиков белки и 10 пакетиков ромашки. При этом ресурсы будут полностью использованы. Прибыль составит 1509 у.е.

Задание 2.

Задача 2.1. Задача коммивояжера.

            Коммивояжеру, находящему в Париже, необходимо посетить три города. Он получил информацию о стоимости перелета в каждый из выбранных городов из Парижа и стоимости перелета из одного города в другой. На основании полученных данных он составил матрицу стоимостей (см. таблицу) перелета в выбранные города и обратно. И теперь ему надо так составить маршрут поездки, чтобы затраты на дорогу были минимальными и чтобы каждый пункт посещался только один раз.

Пункты	Париж	Берлин	Рим	Лондон
Париж	0	270	430	160
Берлин	70	0	160	10
Рим	200	130	0	350
Лондон	210	160	250	0

1.      Экономико-математическая модель задачи.

 

Исходные параметры задачи коммивояжера:

n – количество вылетов;

m – количество прилетов;

a_i – количество вылетов из данного города;

b_j – количество прилетов в данный город; c_ij – стоимость проезда.

Искомые величины:

            x_ij – факт перелета из города A_i в город B_i:

                                ì 0, если из города A_i не перелетали в город B_i,

                        x_ij = î 1, если из города A_i перелетали в город B_i.

                        f(X) – общая стоимость поездок.

             n  m

f(X) =  ∑ ∑ c_ij ∙ x_ij → min,

i=1 j=1

               n

é ∑ x_ij = 1,  i = 1, …, n,

ê  j=1

                  ê   n

          í  ∑ x_ij = 1,  j = 1, …, m,

ê  i=1

ê         ì 0

ë x_ij = î 1, i = 1, …, n, j = 1, …, m.

2.      Поиск оптимального расписания поездок.

 

Решение задачи выполним с помощью надстройки Excel Поиск решения.

Оптимальные значения вектора x_ij, будут помещены в ячейках B3:E6, а оптимальное значение целевой функции – в ячейке B16.

Введем исходные данные. Для того, чтобы компьютер не рассматривал перелет из какого-либо города в этот же город, введем в эти ячейки стоимость билетов гораздо выше основных. Сначала опишем целевую функцию с помощью функции – СУММАПРОИЗВ, а потом введем данные для левых частей ограничений.

 

Исходный рабочий лист Excel.

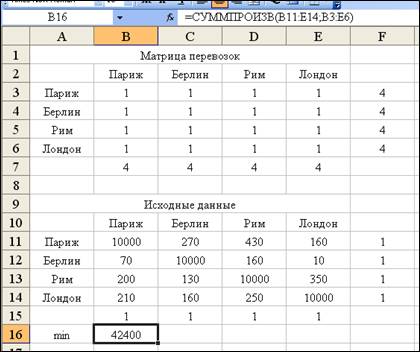
В Поиске решения введем направление целевой функции, адреса искомых переменных, добавим ограничения. Надо учитывать, что переменные x_ij являются булевыми, т.е. могут принимать только значения 1 или 0. На экране появится диалоговое окно Поиска решения с введенными условиями.

Диалоговое окно Поиск решения.

 

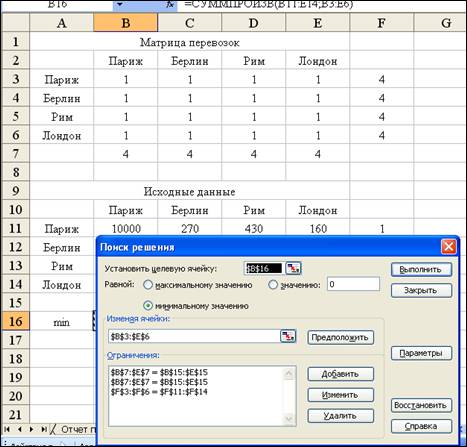
В Параметрах поиска решения установим флажки в окнах Линейная модель и Неотрицательные значения.

Диалоговое окно Параметры поиска решения.

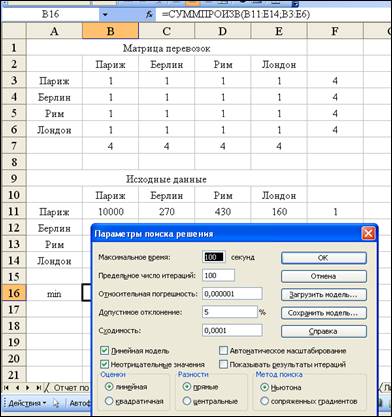
После ввода параметров для решения следует нажать кнопку Выполнить. На экране появится сообщение, что решение найдено.

Диалоговое окно Результаты поиска решения.

 

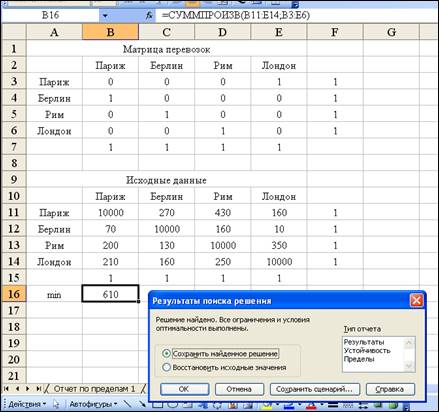
Полученное решение означает, что минимальные затраты будут на маршруте: Париж → Лондон → Рим → Берлин → Париж. Затраты на поездку составят 610.