Задача №1.

Для Вашей компании существуют 4 возможных направления инвестирования капитала:

1. Облигации госзайма, по которым гарантировано 7% дохода. Эти облигации выпускаются на 1 год, т.е. через год все они выкупаются государством.

2. Облигации газовой компании с фиксированным доходом, который будет известен в конце года.

3. Проект А, предполагающий нулевые поступления в течении года и выплаты в конце года, которые будут зависеть от состояния экономики.

4. Проект В, аналогичный проекту А, но с другим распределением выплат.

Требуется оценить ожидаемый доход и риск для всех четырех вариантов и выбрать один из них. Для оценки риска использовать как абсолютный, так и относительный показатель (коэффициент вариации).

Таблица 1.

Доходность	Номер вари-анта	Состояние экономики и их вероятности
Спад (0,10)	Застой (0,30)	Неб. Рост (0,40)	Подъем (0,15)	Бум (0,05)
Облигации госзайма		7,00	7,00	7,00	7,00	7,00
Облигации газовой компании	X4	7,5	8,5	8,0	9,5	10,0
Проект А	X4	-5,5	-4,0	6,0	12,5	24,5
Проект В	X4	-2,0	-1,5	8,0	10,5	11,5

Решение.

1.     Ожидаемый доход рассчитывается по формуле:

Е(Х)=∑Х_i∙Р_i, где

Х_i – предполагаемый доход при ситуации I (определенном состоянии экономики),

Р_i – вероятность ситуации I,

Для первого варианта (облигации госзайма) E(X)=7%.

Для второго варианта (облигации газовой компании) E(X)=7,5∙0,1+ 8,5∙0,3+ 8,0∙0,4+ 9,5∙0,15+ 10,0∙0,05 = 0,75+2,55+3,2+1,425+0,5 = 8,425%.

Для третьего варианта (проект А) E(X)=(–5,5)∙0,1+(–4,0)∙0,3+ 6,0∙0,4+ 12,5∙0,15+ 24,5∙0,05 = –0,55–1,2+2,4+1,875+1,225 = 3,75%.

Для четвертого варианта (проект В) E(X)=(–2,0)∙0,1+ (–1,5)∙0,3+ 8,0∙0,4+ 10,5∙0,15+ 11,5∙0,05 = –0,2–0,45+3,2+1,575+0,575 = 4,7%.

Для первого варианта (облигации госзайма) σ=0.

Для второго варианта (облигации газовой компании) σ=0,676.

Для третьего варианта (проект А) σ=7.85.

Для четвертого варианта (проект В) σ=5.266.

3. Для оценки степени (меры) риска на единицу ожидаемого дохода используется значение коэффициента вариации:

  , где

σ – стандартное отклонение

X – ожидаемое значение дохода (Е(х))

Для первого варианта (облигации госзайма) V=0.

Для второго варианта (облигации газовой компании) V=0.08.

Для третьего варианта (проект А) V=2.09.

Для четвертого варианта (проект А) V=1.12.

Сведем результаты вычислений в таблицу 2.

Таблица 2.

Показатель	Облигации госзайма	Обл. газовой компании	Проект А	Проект В
1. Ожидаемый  доход E(X).	7%	8.425%	3.75%	4.7%
2. Стандартное отклонение σ	0	0.676	7.85	5.26
3. Коэффициент вариации V.	0	0.08	2.09	1.12

Выводы: Человек, который любит рисковать, выбрал бы проект А, как проект, обещающий в случае удачи максимальную прибыль. Человек осторожный предпочел бы облигации газовой компании, т.к. минимальная прибыль по этому проекту наибольшая из всех.

Задача №2.

Выпускник НГАЭиУ рассматривает два варианта трудоустройства:

а) создать малое предприятие и получать доход 3 тыс. у.е. в месяц с вероятностью 60% или 2 тыс. у.е. в месяц с вероятностью 40%;

б) устроиться на работу с фиксированным доходом 2 тыс. у.е. в месяц.

Полезность в зависимости от дохода для выпускника представлена в таблице.

Доход (тыс. у.е.)	X4	1,15	1,25	1,5	2,0	2,05	2,1	3,0
Полезность (у.е.)	X4	1	2	4	5	10	14	19

Необходимо определить какую работу выберет выпускник, максимизирующий полезность?

Чему равна премия за риск?

Решение.

Найдем значения полезности для двух данных видов заработка.

Для варианта а) полезность равна 19∙0.6+5∙0.4=13.4.

Для варианта б) полезность равна 5 (из таблицы).

Отсюда очевидно, что более полезным будет первый вариант (т.к. его полезность больше).

Рассчитаем премию за риск.

Рисковый доход равен 3∙0.6+2∙0.4=2.6 тыс. у.е.

Гарантированный доход равен 2 тыс. у.е.

Следовательно, премия за риск равна 2.6 тыс.  у.е. – 2 тыс. у.е. = 600 у.е.

Задача №3.

Добавочные вложения в расширение производства в размере 50 тыс. у.е. могут увеличить прибыль от реализации продукции со 100 тыс. у.е. до 200 тыс. у.е., при условии, что спрос на нее возрастает.

Эти вложения окажутся напрасными, если спрос не увеличится. Вероятность увеличения спроса, по мнению экспертов предприятия, равна 0,7.

Можно заказать прогноз спроса специализированной фирме, занимающейся изучением рыночной конъюнктуры за 4 тыс. у.е. Как положительный, так и отрицательный прогноз сбываются с вероятностью 0,9.

Необходимо принять решение о целесообразности дополнительных вложений и целесообразности заказа прогноза с целью снижения риска из-за неопределенности (построить «дерево решений» с использованием формулы Байеса).

Решение.

Введем следующие обозначения событий:

Н₁ – событие роста спроса.

Н₂ – событие отсутствия роста спроса.

А – Получение положительного прогноза от фирмы.

А^* – Получение отрицательного прогноза от фирмы.

Запишем исходные данные в принятых обозначениях.

P(H₁)=0.7

P(H₂)=0.3

P(A/H₁)=P(A^*/H₂)=0.9

P(A/H₂)=P(A^*/H₁)=0.1

Найдем вероятность, с которой может быть получен положительный прогноз от фирмы.

P(A)=P(A/H₁)∙P(H₁)+P(A/H₂)∙P(H₂)=0.9∙0.7+0.3∙0.1=0.63+0.03=0.66.

Вероятность получения отрицательного прогноза

P(A^*)=1–P(A)=1–0.66=0.34.

Определим вероятность повышения спроса при положительном прогнозе.

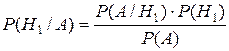 =  = = 0.955

Вероятность отсутствия роста спроса при положительном прогнозе

1–0.955=0.045

Вероятность роста спроса при отрицательном прогнозе

 =  =  = 0.206

Вероятность отсутствия роста спроса при отрицательном прогнозе.

1–0.206=0.794

Сведем воедино все данные для построения дерева решений.

Д₁ – Событие, заключающееся в том, что при положительном прогнозе будет рост спроса. Ожидаемый доход при этом составит 46000 у.е.

Д₂ – Событие, заключающееся в том, что несмотря на положительный прогноз роста спроса не будет. Ожидаемый доход при этом составит  ‑54000 у.е.

E(Д₁,Д₂) – Ожидаемый доход с учетом вероятностей.

E(Д₁,Д₂)= 46000∙0.955+(–54000)∙0.045=43930–2430=41500 у.е.

Д₈ – Событие, заключающееся в том, что будет получен отрицательный прогноз. Ожидаемый доход в этом случае составит  -4000 у.е.

Д₃ - Ожидаемый доход в случае заказа прогноза.

Д₃ = 41500∙0.66+(–4000)∙0.34=27390–1360=26030 у.е.

Д₅ – Событие, заключающееся в том, что при инвестициях без заказа прогноза будет рост спроса. Доход в этом случае составит 50000 у.е.

Д₆ – Событие, заключающееся в том, что при инвестициях без заказа прогноза не будет роста спроса без заказа прогноза. Доход в этом случае составит –50000 у.е.

E(Д₅,Д₆) – Ожидаемый доход с учетом вероятностей.

E(Д₅,Д₆)= 50000∙0.7+(–50000)∙0.3=20000 у.е.

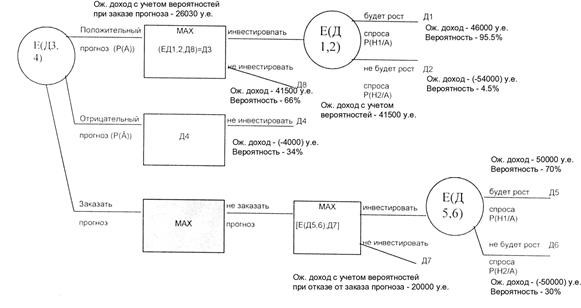
На основании приведенных расчетов можно сделать вывод, что ожидаемый доход в случае заказа прогноза больше, следовательно надо заказывать прогноз в фирме и поступать в соответствии с этим прогнозом.

Задача № 4.

В первых графах таблицы приведены статистические данные о финансовых инструментах А, Б и В. Проанализировать риск этих инструментов (оценить стандартное отклонение и коэффициент вариации), а так же возможных портфелей, когда предприниматель может выбрать одну из двух стратегий:

а) выбрать один из финансовых инструментов;

б) составить портфель, в котором 50% будет составлять один актив, 50% – другой.

Количественные характеристики (годовые %) возможных инвестиций.

Таблица 1.

Год	Вариант	Виды активов	Портфели
А	Б	В	А+Б	Б+В	А+В
1–й	X3	9	13	21	11	17	15
2–й	X3	16	12	23	14	17.5	19.5
3–й	X3	15	12	20	18.5	17.5	16

Исходные характеристики по портфельным инвестициям находятся по формуле средней арифметической взвешенной по данным об инструментах А, Б и В.

Решение.

1.     Среднее значение дохода определяется по формуле.

, где

X_i – текущий доход;

n – число анализируемых периодов.

Найдем среднее значение дохода для всех видов инвестиций.

Активы

А – (9+16+15)/3=13.333.

Б – (13+12+12)/3=12.333

В – (21+23+20)/3=21.333

Портфели

А+Б – (11+14+18.5)/3=14.5

Б+В – (17+17.5+17.5)/3=17.333

А+В – (15+19.5+16)/4=16.833

2. Стандартное отклонение рассчитывается следующим образом:

Активы

A – 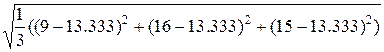=3.091, аналогично

Б – 0.471

В – 1.247

Портфели

А+Б – 3.082

Б+В – 0.236

А+В – 1.929

3. Коэффициент вариации.

Активы

А – 3.091/13.333=0.232

Б – 0.471/12.333=0.038

В – 1.247/21.333=0.058

Портфели

А+Б – 3.082/14.5=0.213

Б+В – 0.2356/17.333=0.014

А+В – 1.929/16.833=0.115

Представим результат в виде таблицы.

Таблица 2.

	Виды активов	Портфели
А	Б	В	А+Б	Б+В	А+В
1. Среднее, %	13.333	12.333	21.333	14.5	17.333	16.833
2. Стандартное отклонение, %	3.091	0.471	1.247	3.082	0.236	1.929
3. Коэффициент вариации.	0.232	0.038	0.058	0.213	0.014	0.115

4. При таком выборе явно более предпочтительным является вариант В, т.к. доход по нему и при благоприятных и при неблагоприятных условиях максимальный.

Задача № 5.

В портфеле предприятия «Сибин» находится 2 вида акций с разными среднегодовыми нормами доходности ­– акции «А» и акции «Б» с соответствующими характеристиками абсолютного размера риска в виде дисперсий D(А) и D(Б). Линейный коэффициент корреляции текущих норм доходности акций «А» и «Б» равен –1. (R=–1).

Вариант	Среднегодовая норма доходности	Абсолютный размер риска
акции А	акции Б	σ2А	σ(А)	σ2Б	σ(Б)
X4	13,5	17,0	21,5	4,64	192,3	13,86

Найти пропорцию распределения денежных средств, инвестируемых в акции, соответствующих минимуму риска (нулевой дисперсии).

Решение.

1. Величина доли инвестиций в акции задается произвольно (в данном случае с шагом 0,2).

2. Средняя норма доходности акций в портфеле (доходность портфеля) рассчитывается как

E(x,n)=∑h_iX_i , где

h_i – доля i-ой бумаги в портфеле.

X_i – норма доходности i-ой бумаги.

3. Величина портфельного риска определяется по формуле:

σ²=h²_А∙ σ²_А+ h²_Б∙ σ²_Б+2∙R∙h_А∙σ_А∙h_Б∙σ_Б, где

σ²_А,Б – дисперсия доходности акций А, Б.

R=–1 – значение коэффициента корреляции текущих норм доходности акций А, Б;

σ_А,Б – стандартное отклонение норм доходности акций А,Б.

Решение представим в виде таблицы:

Принимаемая в расчет доля инвестиций в акции	Средняя норма доходности акций в портфеле	Величина портфельного риска
nА	nБ	E(x,n)	σ2(n)
1	0	13.5	21.5
0,8	0,2	14.2	0.872
0,6	0,4	14.9	7.639
0,4	0,6	15.6	41.799
0,2	0,8	16.3	103.353
0	1	17	192.3

Минимальная величина портфельного риска (0.872) будет при следующем распределении инвестиций 80% акций А и 20% акций Б.