1. В урне 14 билетов. Из них
5 выигрышных. Какова вероятность того, что первый вынутый билет окажется
выигрышным.
Решение:
Искомая вероятность равна отношению
исходов, благоприятных событию «Вынутый билет выигрышный» к числу всех
возможных событий, т.е. 5/14=0.357
или 35,7%.
2. Биатлонист стреляет в
мишень. Мишень – круг радиуса 9 см. Биатлонист попадает в мишень с вероятностью
1. Попадание в любую точку мишени равновероятно. Необходимо попасть в круг
радиуса 5 см.
Решение:
Согласно определению геометрической
вероятность попадания в круг радиуса 5 см равна 5/9=0,556, или 55,6%.
3. Имеется собрание
сочинений из 7 томов некоторого автора. Все 7 томов расставляются на книжной
полке случайным образом. Какова вероятность того, что тома расположатся в
порядке 1, 2, 3, 4, 5, 6, 7 или 7, 6, 5, 4, 3, 2, 1.
Решение:
В том и в другом случае ответ будет
одинаков, поэтому рассмотрим только случай расположения в порядке 1, 2, 3, 4,
5, 6, 7. Том №1 на первом месте оказывается с вероятностью 1/7; при условии, что первый том занял
место №1, второй том занимает место №2 с вероятностью 1/6; аналогично при условии, что тома №1
и №2 заняли соответственно места №1 и №2, третий том занимает место №3 с
вероятностью 1/5 и т.д.
Тогда, по теореме о произведении вероятностей независимых событий, тома
располагаются в порядке 1, 2, 3, 4, 5, 6, 7 с вероятностью
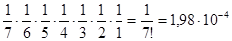 .
.
4. Имеется собрание
сочинений из 9 томов некоего автора. На верхней полке умещается только 6 томов.
Это тома берут из 9 томов случайным образом и расставляют на верхней полке
случайным порядком. Какова вероятность того, что тома расположатся в порядке 1,
2, …, 7 или 7, 6, …, 1?
Решение:
Найдем вероятность того, что тома
расположатся в порядке 1, 2, …, 7.
Первой поставленной книгой должен
быть только первый том, т.е. общее число исходов – 9, а число благоприятных
исходов – 1. Следовательно вероятность того, что первый том окажется на первом
месте равна 1/9.
Аналогично получим, что вероятность
того, что второй том будет стоять на втором месте равна 1/8, что третий том
будет стоять на третьем месте – 1/7 и т.д.
Вероятность того, что тома
расположатся в порядке 1, 2, …, 7 будет равна
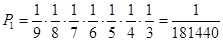 .
.
Аналогично найдем вероятность того,
что тома расположатся в порядке 7, 6, …, 1.
Проведя аналогичные рассуждения
получим, что P2=P1.
Искомая вероятность равна 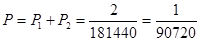 .
.
5. Имеется собрание
сочинений из 9 томов некоего автора. На верхней полке умещается только 7 томов.
Это тома берут из 9 томов случайным образом и расставляют на верхней полке случайным
порядком. Какова вероятность, что для размещения на полке будут выбраны тома 1,
2, …, 7?
Решение:
Вероятность того, что первый наугад
выбраны том попадет в число нужных равна 7/9. Для второго тома эта вероятность
равна 6/8, для третьего 5/7 и т.д. В итоге получим:
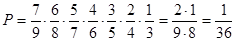 .
.
6. Три стрелка стреляют по мишени.
Предполагается, что события попадания в мишень для стрелков независимы и
вероятности попадания стрелков в мишень равны 0,4; 0,3; 0,2. Какова вероятность
того, что:
а) все три выстрела окажутся
успешными;
б) хотя бы один из трех выстрелов
окажется успешным;
в) точно один выстрел окажется
успешным?
Решение:
а) По теореме о произведении
вероятностей независимых событий искомая вероятность 0,4·0,3·0,2=0,024.
б) Заметим, что если первый выстрел
оказывается успешным с вероятностью 0,4, то этот выстрел оказывается неуспешным
с вероятностью (1–0,4). Событий «хотя бы один из трех выстрелов окажется
успешным» предполагает, что точно какой-нибудь один из трех выстрелов успешен
(два остальных неуспешны), либо только каких-нибудь два из трех выстрелов
успешны (один неуспешен), либо все три успешны. Тогда, по теореме о сумме
независимых событий искомая вероятность равна
[0,4·(1-0,3)·(1-0,2)+ (1-0,4)·0,3·(1-0,2)+ (1-0,4)·(1-0,3)·0,2] + [0,4·0,3·(1-0,2)+ (1-0,4)·0,3·0,2+ +0,4·(1-0,3)·0,2] + [0,4·0,3·0,2] = 0,452 + 0,188 + 0,024 = 0,664.
в) 0,4·(1-0,3)·(1-0,2)+ (1-0,4)·0,3·(1-0,2)+ (1-0,4)·(1-0,3)·0,2 = 0,452.
7. Идет охота на волка. В охоте
участвуют 4 охотника. Вероятность выхода волка на первого охотника – 0,3; на
второго – 0,2; на третьего – 0,1; на четвертого – 0,4. Вероятность убийства
волка первым охотником, если волк вышел на него – 0,8. Вероятность убийства
волка вторым охотником, если волк вышел на него – 0,7. Вероятность убийства
волка третьим охотником, если волк вышел на него – 0,6. Вероятность убийства
волка четвертым охотником, если волк вышел на него – 0,9. Какова вероятность
убийства волка?
Решение:
По формуле полной вероятности
искомая вероятность
Р = 0,3·0,8 + 0,2·0,7 + 0,1·0,6 +
0,4·0,9 = 0,8.
8. 14% всех мужчин и 5% всех
женщин – дальтоники. Наугад выбранное лицо оказалось дальтоником. Какова
вероятность того, что это мужчина. Число мужчин и женщин считается одинаковым.
Решение:
Введем следующие обозначения
событий:
A1 – выбранный человек – мужчина.
A2 – выбранный человек – женщина.
B – выбранный человек – дальтоник.
Во введенных обозначениях получим: P(A1)=0,5; P(A2)=0,5; P(B/A1)=0,14; P(B/A2)=0,05.
По формуле полной вероятности
получим, что вероятность того, что выбранный человек окажется дальтоником,
равна:
P(B)=P(A1)∙P(B/A1)+ P(A2)∙P(B/A2)=0,5∙0,14+0,5∙0,05=0,07+0,025=0,095.
Искомую вероятность найдем по
формуле Байеса.
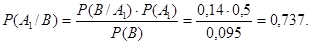
9. Случайная величина X
задана рядом распределения.
|
X
|
–3
|
0
|
1
|
4
|
|
P
|
0.4
|
0.3
|
0.2
|
0.1
|
Найти математическое ожидание MX, дисперсию DX, σx,
вероятности P(X<0), P(X>0), P(–1<X<3).
Y=2X+b. Найти математическое
ожидание MY, дисперсию DY.
Решение:
MX=(–3)∙0.4+0∙0.3+1∙0.2+4∙0.1=–0.12+0.2+0.4=0.48.
DX=(–3-0.48)2∙0.4+(0-0.48)2∙0.3+(1-0.48)2∙0.2+(4-0.48)2∙0.1 = 6.21
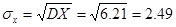
P(X<0)=P(X=–3)=0.4
P(X>0)=P(X=1)+P(X=4)=0.2+0.1=0.3
P(–1<X<3)=P(X=0)+P(X=1)=0.3+0.2=0.3
Y=2X+b. Составим для величины Y ряд распределения.
|
Y
|
–6+b
|
b
|
2+b
|
8+b
|
|
P
|
0.4
|
0.3
|
0.2
|
0.1
|
MY=M(2X+b)=2MX+b=2∙0.48+b=0.96+b
DY=D(2X+b)=D(2X)+D(b)=D(2X)=4DX=4∙6.21=24.83.
10. Футболист бьет 5 раз
пенальти. Вероятность забить при одном ударе – 0.5. Какова вероятность того,
что будет забито 3 мяча? Более 2? Найти математическое ожидание MX, дисперсию DX.
Решение:
Найдем вероятность того, что будет
забито 3 мяча.
P(X=3) = C35∙0.53∙(1-0.5)5-3
= 10∙0.125∙0.25 = 0.3125.
Найдем вероятность того, что будет
забито более двух мячей.
Дополнительным событием к искомому
будет событие, что забито 0,1 или 2 мяча. Найдем вероятность каждого из этих событий.
P(X=0) = C05∙0.50∙0.55
= 0.55 = 0.03125.
P(X=1) = C15∙0.51∙0.54
= 6∙0.2∙0.32768 = 0.15625.
P(X=2) = C25∙0.52∙0.53
= 10∙0.03125 = 0.3125.
Получаем, вероятность того что
будет забито 2 мяча или меньше равна 0.03125+0.15625+0.3125 = 0.5.
Искомая вероятность (вероятность
того, что будет забито более двух мячей) равна
1–0.5 = 0.5.
MX=np=5∙0.5
= 2.5.
DX=np(1–p)= 5∙0.5∙0.5 = 1.25.
11. Количество X принимаемых
за час звонков по домашнему телефону имеет распределение Пуассона. Среднее
количество принимаемых за час звонков – 5. Какова вероятность того, что будет
принято 3 звонка? Более 2? Найти математическое ожидание MX, дисперсию DX.
Решение:
Найдем вероятность того, что будет
принято 3 звонка.
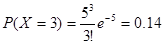
Найдем вероятность того, что будет
принято более двух звонков.
Дополнительным событием к искомому
будет событие, что принято 0,1 или 2 звонка. Найдем вероятность каждого из этих
событий.
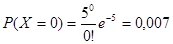
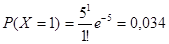
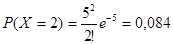
Получаем, вероятность того что будет
принято 2 звонка или меньше равна 0.007+0.034+0.084 = 0.125.
Искомая вероятность (вероятность
того, что будет принято более двух звонков) равна 1–0.125 = 0.875.
12. Функция плотности
случайной величины X имеет вид:
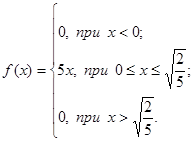
Найти математическое ожидание MX, дисперсию DX, P(0<X<0.1)
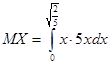 =
= 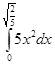 =
= 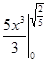 =
= 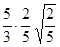 =
= 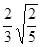 .
.
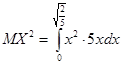 =
= 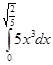 =
=  =
= 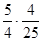 =
= 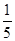 .
.
DX=MX2–(MX)2 = 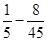 = 0,022.
= 0,022.
P(0<X<0.1)= 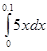 =
= 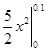 =
2,5∙0.01 = 0.025.
=
2,5∙0.01 = 0.025.
13. Случайная величина X – время ожидания дождя в
сутках – имеет равномерное распределение на отрезке [0;5]. Найти математическое
ожидание MX, дисперсию DX, вероятности P(X<5),
P(X>3).
Решение:
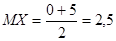
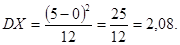
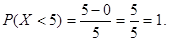
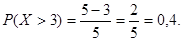
14. Вероятность безотказной
работы прибора в течении x
часов равна e–0.005x. Найти математическое ожидание MX – среднюю наработку на отказ и
вероятность безотказной работы прибора в течение 100 часов.
Решение:
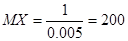
Вероятность безотказной работы
прибора в течении 100 часов равна
P(X>100) = e-0.005∙100 = e-0.5 = 0.61.
15. Случайная величина x
имеет нормальное распределение N(5;5). Математическое ожидание MX = 5, среднеквадратическое отклонение – 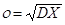 = 5.
Найти P(X<1), P(–1<X<1), P(–5<x<5),
P(–8<X–26<8) , P(–16<X–26<16) , P(–24<X–26<24).
= 5.
Найти P(X<1), P(–1<X<1), P(–5<x<5),
P(–8<X–26<8) , P(–16<X–26<16) , P(–24<X–26<24).
Решение:
P(X<1)
= 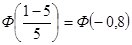 = 0.2119.
= 0.2119.
P(–1<X<1)
= 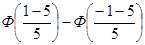 =
= 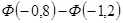 = 0.2119 – 0.1151 =
0.0968.
= 0.2119 – 0.1151 =
0.0968.
P(–5<X<5)
= 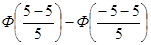 =
= 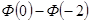 = 0.5 – 0.0228 = 0.4772.
= 0.5 – 0.0228 = 0.4772.
P(–5<X–5<5
= 2Ф(1) = 0.6826.
P(–10<X–5<10)
= 2Ф(2) = 0.9544.
P(–15<X–26<15)
= 2Ф(3) = 0.9973.
16. Вес мужчины – случайная
величина со средним 80 кг и дисперсией 30. Оценить с помощью неравенства
Чебышева вероятность того, что вес случайно встреченного мужчины отличается от
среднего на величину, большую 14.
Решение:
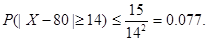
17. Вероятность детали быть
бракованной равна 0.005. Произведено 1000 деталей. Какова вероятность того, что
в этой партии точно 2 бракованных детали? Более 2?
Решение:
λ = np = 1000∙0.005 = 5.
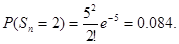
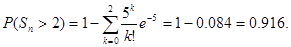
18. Игральную кость бросают
600 раз. Какова вероятность того, что число выпадений шестерки будет между 84 и
116.
Решение.
Искомая вероятность будет равна
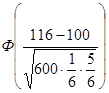 –
– 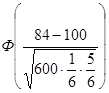 =
= 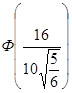 –
– 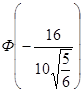 = Ф(1.75) – Ф(–1.75) =
= 0.9599 – 0.0401 = 0.9198.
= Ф(1.75) – Ф(–1.75) =
= 0.9599 – 0.0401 = 0.9198.