1. Если множество 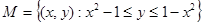 , то: а)
, то: а) 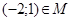 ; б)
; б) 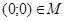 ; в)
; в) 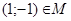 ; г)
; г) 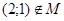 . Какие из вышеперечисленных высказываний истинны, а какие
ложны?
. Какие из вышеперечисленных высказываний истинны, а какие
ложны?
Решение:
а) 4–1£1£1–4
– неверно, т.е. утверждение ложно.
б) 0–1£1£1–0
– верно, утверждение истинно.
в) 1–1£1£1–1 – неверно, т.е. утверждение
ложно.
г) 4–1£1£1–4
– неверно, т.е.
утверждение ложно.
2. Истины ли высказывания:
а) (A \ B) È (B \ A) = (A È B) \ (A Ç B);
б) A \ (A \ B) = A Ç B.
Решение:
а) Пусть хÎ(A \ B) È (B \ A). Докажем, что хÎ(A È B) \ (A Ç B).
Т.к. хÎ(A \ B) È (B \ A), то хÎ(A \ B) и хÎ (B \ A); т.к. хÎ(A \ B), то хÎA и хÏВ; т.к. хÎ (B \ A), то хÎВ
и хÏА.
Утверждения (хÎA и хÏВ) и (хÎВ
и хÏА)
могут быть верны тогда и только тогда, когда (хÎА и хÎВ)
и (хÏА
и хÏВ),
т.е. хÎ(A È B)
и хÏ(A Ç B). Таким образом доказали,
что если хÎ(A \ B) È (B \ A), то хÎ(A È B) \ (A Ç B). Это означает, что (A \ B) È (B \ A) Í
(A \ B) È (B \ A).
Аналогичным образом можно доказать,
что (A \ B) È (B \ A) Í
(A \ B) È (B \ A).
Значит, можно доказать, что (A \ B) È (B \ A) = (A \ B) È (B \ A), т.о. первое
утверждение верно.
б) Пусть хÎ A \ (A \ B). Это значит, что хÎА
и (хÏA \ B); т.е. хÎА и хÎВ;
последнее означает, что хÎA
и хÎВ,
т.е. хÎA Ç B. Это, в свою очередь,
означает, что доказали включение A \ (A \ B) Í A Ç B.
Аналогично можно доказать, что A Ç B Í
A \ (A \ B).
Значит, можно доказать, что A Ç B = A \ (A \ B), т.е. второе утверждение
верно.
3. Найти область определения
функции 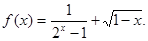
Решение:
Область определения функции – это
множество множество точек на числовой прямой, в которых имеет смысл каждое
действие, указанное в формуле, задающей функцию.
Т.к. в формулу входит радикал, то
значение под ним не может быть отрицательным, т.е. 1–х ≥0 или 1≥х.
Т.к. в формулу входит дробь, то ее
знаменатель не должен обращаться в 0. Найдем точки, в которых знаменатель дроби
обращается в 0.
2х–1=0
2х =1
x=0.
С учетом всего вышеизложенного
получим область определения функции.
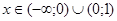 .
.
4. Проведенное среди
школьников анкетирование показало, что в шахматы умеют играть 35 человек, в
шашки – 40 человек, причем в обе игры умеют играть 21 человек. Сколько человек
не умеют играть ни в шахматы, ни в шашки.
Решение:
В задаче не хватает данных, т.к. не
указано, сколько человек учится в школе. Пусть в школе 100 учеников (задаем
произвольно, иначе задачу решить нельзя). Тогда 35 – 21 = 14 человек умеют
играть только в шахматы; 40 – 21 = 19 человек умеют играть только в шашки.
Окончательно не умеют играть ни в шахматы, ни в шашки 100 – 14 – 19 – 21 = 46
человек не умеют играть ни в шашки, ни в шахматы.
5. Обозначим через А –
множество всех квадратов, площадь которых равна 1; через В – множество всех
равносторонних треугольников единичной площади. Каждому квадрату из А ставят в
соответствие треугольник из В. Является ли это соответствие взаимнооднозначным?
Решение:
Множество А состоит только из
одного квадрата, а именно, квадрата со стороной 1.
Пусть равносторонний треугольник
имеет сторону длиной х. Тогда его площадь равна 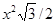 . Но уравнение
. Но уравнение 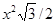 =1 имеет единственный корень, имеющий физический смысл;
значит, существует только один равносторонний треугольник площади 1, а именно
треугольник сто стороной
=1 имеет единственный корень, имеющий физический смысл;
значит, существует только один равносторонний треугольник площади 1, а именно
треугольник сто стороной 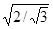 , т.е. множество В также состоит из одного элемента.
, т.е. множество В также состоит из одного элемента.
Между двумя множествами, состоящими
из одного элемента, можно установить взаимнооднозначное соответствие, т.е.
соответствие, при котором квадрату из А ставят в соответствие треугольник из В,
является взаимнооднозначным.
6. Правильно ли рассуждение,
имеющее форму: «Все x являются y и некоторые у являются z; значит, все z не
являются х»?
Решение:
Это рассуждение неверно, т.к.
существует некоторое множество элементов, которые являются и х, и у, и z; значит, некоторые я
являются х.
7. Рассмотрим пары
действительных чисел вида (a;b).
Пары (a;b) и (c;d) будем считать равными в
том и только в том случае, если а=с и b=d. Определим сложение пар с помощью тождества (a;b)+(c;d)=(а+с;b+d). Проверить, что множество пар (a;b) с операцией сложения
является коммутативной группой.
Решение:
Проверим является ли это множество
группой. Для этого необходимо проверить три условия:
1) ассоциативность.
(((a1;b1)+(a2;b2))+(a3;b3))=((a1;b1)+((a2;b2)+(a3;b3)))
Это условие выполняется. Обе части
равенства равны (a1+a2+a3;b1+b2+b3).
2) Единичным элементом будет пара
(0;0).
(a;b)+(0;0)=(0;0)+(a;b)=(a;b).
3) Обратным элементом для элемента
(aжb) будет элемент (–a;–b)
(a;b)+(–a;–b)=(–a;b)+(a;b)=(0;0).
Для того, чтобы данное множество
являлось коммутативной группой, необходимо выполнение условия коммутативности,
т.е.
(a1;b1)+(a2;b2)=(a2;b2)+(a1;b1)
Это условие выполняется в силу коммутативности сложения
действительных чмсел..