ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КОНТРОЛЬНАЯ РАБОТА № 1
по дисциплине «Математический анализ и линейная
алгебра»
7 вариант
Исполнитель:
специальность Ф и К
группа
№ зачетной книжки
Руководитель:
Борисова Вера Ионовна
Серпухов - 2006
Задание 1. Решить уравнение методом Гаусса.
|
5
|
3
|
-1
|
1
|
2
|
|
2
|
-1
|
1
|
2
|
14
|
|
4
|
-1
|
2
|
-1
|
0
|
|
3
|
-1
|
3
|
3
|
12
|
|
|
|
|
|
|
5
|
3
|
-1
|
1
|
2
|
|
0
|
-2,2
|
1,4
|
1,6
|
13,2
|
|
0
|
-3,4
|
2,8
|
-1,8
|
-1,6
|
|
0
|
-2,8
|
3,6
|
2,4
|
10,8
|
|
|
|
|
|
|
5
|
3
|
-1
|
1
|
2
|
|
0
|
-2,2
|
1,4
|
1,6
|
13,2
|
|
0
|
0
|
0,636364
|
-4,27273
|
-22
|
|
0
|
0
|
1,818182
|
0,363636
|
-6
|
|
|
|
|
|
|
5
|
3
|
-1
|
1
|
2
|
|
0
|
-2,2
|
1,4
|
1,6
|
13,2
|
|
0
|
0
|
0,636364
|
-4,27273
|
-22
|
|
0
|
0
|
0
|
12,57143
|
56,85714
|
|
|
|
|
|
|
|
|
X4 =
|
4,522727
|
|
|
|
X3 =
|
-4,20455
|
|
|
|
X2 =
|
-5,38636
|
|
|
|
X1 =
|
1,886364
|
Преобразуем в матрицу, и
далее сокращая получаем значение х1,х2,х3,х4.
Задание 2.
Limx->0(g(y)/f(x)) = Limx->0(g’(y)/f’(x))
Limx->0((e2x-e-x-3x)/x2)
= Limx->0((2e2x+e-x-3)/2x)
= Limx->0((4e2x-e-x)/2)
= 3/2
Задание 3.
Y’ = (((log2(X2+3))/(1+x3))1/3)’ =
1/3(((log2(X2+3))/(1+x3))-2/3)(((log2(X2+3))/(1+x3))’)
=
1/3(((log2(X2+3))/(1+x3))-2/3)(((log2(X2+3))’(1+x3)-((log2(X2+3))(1+x3)’)/(1+x3)2
=
1/3(((log2(X2+3))/(1+x3))-2/3)((((2X)/((X2+3)ln2))(1+x3)-((log2(X2+3))(3x2))/(1+x3)2
Задание 4.
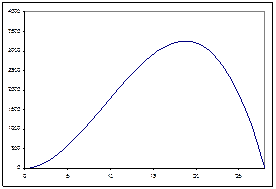
X+Y=28
X2Y=max
ð
X2(28-X)=max (или Z= Xmax2(28- Xmax), в диапазоне X от 0 до 28)
ð
Максимум этой
функции ищем по производной
ð
56Xmax-3Xmax2=0
ð
Xmax=56/3
Задание 5.
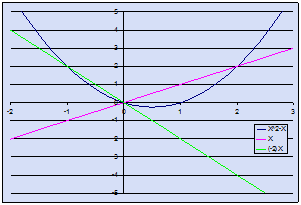
Y=X2-X
Y=2 => X2-X-2=0;
X1,2=2;-1.
Уравнения прямых проходящих
через начало координат
Y=aX
Отсуда находим a1,2=1;-2.
Или Y=X; Y=-2X.
Задание 6
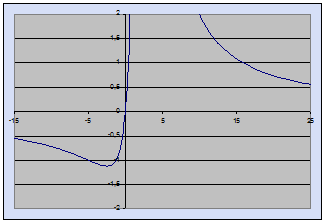
Lim(x->+∞)=(45/(2(5-2X)(-2))=0(+)
Lim(x->-∞)=(45/(2(5-2X)(-2))=0(-)
Lim(x->+5/2)=(45/(2(5-2X)(-2))=∞(+)
Lim(x->-5/2)=(45/(2(5-2X)(-2))=∞(+)
X=0 -> Y=0
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КОНТРОЛЬНАЯ РАБОТА № 2
по дисциплине «Математический анализ и линейная
алгебра»
7 вариант
Исполнитель:
специальность Ф и К
группа
№ зачетной книжки
Руководитель:
Борисова Вера
Ионовна
Серпухов - 2006
Задание 1.
Int((X(1-X1/2))-1/2dX) = Int((Y-1(1-Y))-1/2dY2) = Int(((Y-1(1-Y))-1/2)2YdY) =
Int(((1-Y)-1/2)2dY) = -2Int(((1-Y)-1/2)d(1-Y))
= -4(1-Y)1/2 = -4(1-X1/2)1/2
Задание 2.
ln40Int((2X+5)eX/2dX) = ½ Int((2X+5)deX/2) = ½ ((2X+5)eX/2)
- ½ Int(eX/2d(2X+5)) =
½ ((2X+5)eX/2) - ½ Int(eX/2dX/2)
= ½ ((2X+5)eX/2) - ½ eX/2
Определённый интеграл от ln4 до 0 равен:
ln4 | ½ ((2X+5)eX/2) -
½ eX/2 = ½ ((2ln4+5)eln4/2) -
½ eln4/2 =
½ ((2ln4+5)√4)
- ½ √4 = 2ln(4)+4
0
| ½ ((2X+5)eX/2) - ½ eX/2
=½ (5) - ½ = 4
ln40Int = 2ln(4) = 2,772589
Задание 3.
641Int(2(X1/2+1)2(X-1/3))dX = (заменяем X = t6)
= Int(2(t3+1)2(t-2))dt6
= 12Int( t3+1)2(t-2)(t5)dt = 12Int( t3+1)2(t3)dt = 12Int( t9+2t6+t3)dt = 12( t10/10+2t7/7+t4/4)
Если X=64 –> t =2, X=1 –> t =1
ð 641Int(2(X1/2+1)2(X-1/3))dX = 12( 210/10+28/7+24/4)
- 12( 1/10+2/7+1/4) =
12(1023/10+254/7+15/4) = 1708,029
Задание 4.
X2Y’ + 2XY – 1 = 0;
Уравнение имеет множество
частных решений.
Преобразуем:
Y’+2Y/X-1/X2=0;
заменим Y=UV => Y’=U’V+UV’
U’V+UV’ + 2UV/X – 1/X2=0;
U’V + U(V’+2V/X) – 1/X2=0;
Найдём одно из частных
решений, допустим V’+2V/X=0
dV/dX=-2V/X
тогда dV/V=-2dX/X, проинтегировав и приняв С=0 получаем lnV=lnX-2 => V=X-2
Подставляя в уравнение (U’V + U(V’+2V/X) – 1/X2=0;)
получаем
U’/X2 – 1/X2=0;
U’ = X;
=> U= X + C;
=> Y=UV= (X+C)/X2 = 1/X + C/X2
Задание 5.
Вычислить площадь фигуры
ограниченной линиями Y2=1-X, X=-3.
Преобразуем Y=±√(1-X), X=-3
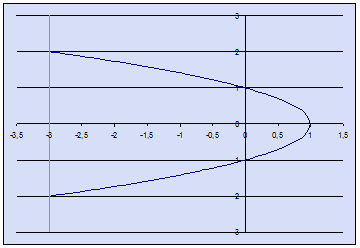
S = 2(-31Int√(1-X)dX)
= -2(-31Int(1-X)1/2d(1-X))= -31|-(4/3)(1-X)3/2=32/3
= 10,66667
Задание 6.
|
Xi
|
Yi
|
Y=(X+2)1/4
|
|
14
|
2,1
|
2
|
|
18
|
2,2
|
2,114743
|
|
22
|
2,5
|
2,213364
|
|
26
|
2,8
|
2,300327
|
|
32
|
2,9
|
2,414736
|
|
A
|
0,04918033
|
0,022912
|
|
B
|
1,39836066
|
1,695404
|
|
Yi(МНК)
|
Y=(X+2)1/4(МНК)
|
|
14
|
2,086885
|
2,016173
|
|
18
|
2,283607
|
2,107821
|
|
22
|
2,480328
|
2,199469
|
|
26
|
2,677049
|
2,291117
|
|
32
|
2,972131
|
2,42859
|
|
Точки пересечения перпендикуляров к линейным
зависимостям для одной и другой функции
|
|
A
|
B
|
|
|
|
Xi
|
Yi
|
Xi
|
Y=(X+2)1/4
|
Растояние
A
|
Растояние
B
|
|
14,13333
|
2,093443
|
13,64707
|
2,008086
|
0,133494
|
0,353021
|
|
17,15
|
2,241803
|
18,15105
|
2,111282
|
0,851027
|
0,151088
|
|
22,2
|
2,490164
|
22,30322
|
2,206416
|
0,200242
|
0,303299
|
|
27,25
|
2,738525
|
26,20097
|
2,295722
|
1,251511
|
0,201025
|
|
31,26667
|
2,936066
|
31,69769
|
2,421663
|
0,73422
|
0,302391
|
|
Сумма квадратов расстояний
от точек до линейных приближений
|
2,887523
|
0,371294
|
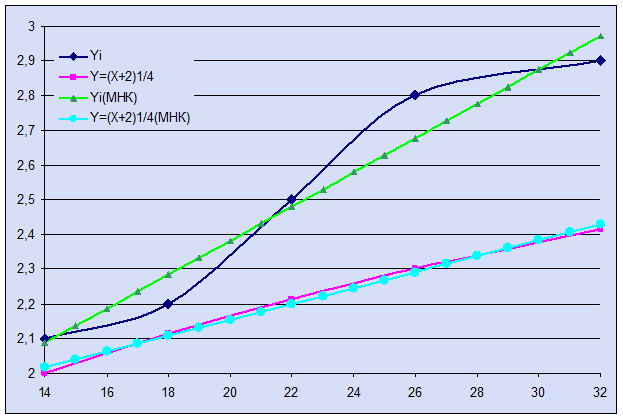
Задание 7.
0,20Int(ln(1+X2)dX)
Разложение функции в ряд Маклорена
ln(1+X2) = ln(1+Y)
= Y – Y2/2 + Y3/3 - … + (-1)nY(n+1)/(n+1)
+ …=
X2 – X4/2 + X5/3 - … + (-1)nX(n+3)/(n+1) + …
После интегрирования получаем
X3/3 – X5/10 + X6/18 - … + (-1)nX(n+4)/((n+1)(n+4)) + …
0,20Int(ln(1+X2)dX) = 0,23/3 – 0,25/10 + 0,26/18
- … + (-1)n0,2 (n+4)/((n+1)(n+4)) + …
Суммируя 2 члена, так чтобы
они были положительны
(-1)n0,2 (n+4)/ ((n+1)(n+4))-(-1)n0,2 (n+5)/((n+2)(n+5))
Пренебрегая некоторыми
константами, получаем:
0,2(n+4) /kn2, где k-константа,
Если учесть, что при
увеличении n каждый последующий член
уменьшается на порядок, то число n=1, даёт
точность ниже 0,001
Получаем
0,20Int(ln(1+X2)dX) = 0,2 3/3 – 0,2 5/10 + 0,2 6/18
- 0,2 (3+4)/((3+1)(3+4)) + 0,2 (4+4)/((4+1)(4+4)) -0,2
(5+4)/((5+1)(5+4)) + 0,2 (6+4)/((6+1)(6+4))
При n=1: 0,00266667
При n=2: 0,002634667
При n=3: 0,002638222
При n=4: 0,002637765