4. Имеется собрание сочинений из 10 томов некоего автора. На
верхней полке умещается только 6 томов. Это тома берут из 10 томов случайным
образом и расставляют на верхней полке случайным порядком. Какова вероятность
того, что тома расположатся в порядке 1, 2, …, 6 или 6, 5, …, 1?
Решение.
Найдем вероятность того, что тома расположатся в порядке 1,
2, …, 6.
Первой поставленной книгой должен быть только первый том,
т.е. общее число исходов – 10, а число благоприятных исходов – 1. Следовательно
вероятность того, что первый том окажется на первом месте равна 1/10.
Аналогично получим, что вероятность того, что второй том
будет стоять на втором месте равна 1/9, что третий том будет стоять на третьем
месте – 1/8 и т.д.
Вероятность того, что тома расположатся в порядке 1, 2, …, 6
будет равна
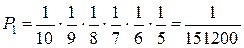
Аналогично найдем вероятность того, что тома расположатся в
порядке 6, 5, …, 1.
Проведя аналогичные рассуждения получим, что P2=P1.
Искомая вероятность равна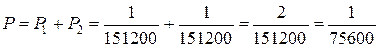 
5. Имеется собрание сочинений из 10 томов некоего автора. На
верхней полке умещается только 6 томов. Это тома берут из 10 томов случайным
образом и расставляют на верхней полке случайным порядком. Какова вероятность,
что для размещения на полке будут выбраны тома 1, 2, …, 6?
Решение.
Вероятность того, что первый наугад выбраны том попадет в
число нужных равна 6/10. Для второго тома эта вероятность равна 5/9, для
третьего 4/8 и т.д. В итоге получим:
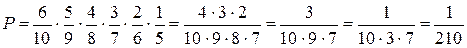
8. 6% всех мужчин и 35% всех женщин – дальтоники. Наугад
выбранное лицо оказалось дальтоником. Какова вероятность того, что это мужчина.
Число мужчин и женщин считается одинаковым.
Решение.
Введем следующие обозначения событий:
A1
– выбранный человек – мужчина.
A2
– выбранный человек – женщина.
B – выбранный
человек – дальтоник.
Во введенных обозначениях получим.
P(A1)=0.5
P(A2)=0.5
P(B/A1)=0.06
P(B/A2)=0.35
По формуле полной вероятности получим:
P(B)=P(A1)∙P(B/A1)+
P(A2)∙P(B/A2)=0.5∙0.06+0.5∙0.35=0.03+0.175=0.205
Искомую вероятность найдем по формуле Байеса.
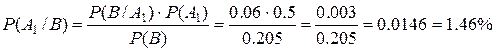
9. Случайная величина X задана рядом распределения.
|
X
|
–3
|
0
|
1
|
4
|
|
P
|
0.3
|
0.2
|
0.1
|
0.4
|
Найти математическое ожидание MX, дисперсию DX, σx, вероятности
P(X<0), P(X>0), P(–1<X<3).
Y=2X+b. Найти математическое ожидание MY, дисперсию DY.
Решение.
MX=(–3)∙0.3+0∙0.2+1∙0.1+4∙0.4=–0.9+0.1+1.6=0.8
DX=(–3-0.8)2∙0.3+ (0-0.8)2∙0.2+ (1-0.8)2∙0.1+ (4-0.8)2∙0.4 = 14.44∙0.3+ 0.64∙0.2+ 0.04∙0.1+ 10.24∙0.4 = 4.332+ 0.128+ 0.004+ 4.096 =
8.56
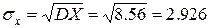
P(X<0)=P(X=–3)=0.3
P(X>0)=P(X=1)+P(X=4)=0.1+0.4=0.5
P(–1<X<3)=P(X=0)+P(X=1)=0.2+0.1=0.3
Y=2X+b. Составим для величины Y ряд распределения.
|
Y
|
–6+b
|
b
|
2+b
|
8+b
|
|
P
|
0.3
|
0.2
|
0.1
|
0.4
|
MY=M(2X+b)=2MX+b=2∙0.8+b=1.6+b
DY=D(2X+b)=D(2X)+D(b)=D(2X)=4DX=4∙8.56=34.24
10. Футболист бьет 6 раз пенальти. Вероятность забить при
одном ударе – 0.2. Какова вероятность того, что будет забито 3 мяча? Более 2?
Найти математическое ожидание MX,
дисперсию DX.
Решение.
Найдем вероятность того, что будет забито 3 мяча.
P(X=3) = C36∙0.23∙0.83
= 20∙0.008∙0.512 = 0.08192 = 8.192%
Найдем вероятность того, что будет забито более двух мячей.
Дополнительным событием к искомому будет событие, что забито
0,1 или 2 мяча. Найдем вероятность каждого из этих событий.
P(X=0) = C06∙0.20∙0.86
= 0.86 = 0.262144
P(X=1) = C16∙0.21∙0.85
= 6∙0.2∙0.32768 = 0.393216
P(X=2) = C26∙0.22∙0.84
= 15∙0.04∙0.4096 = 0.24576
Получаем, вероятность того что будет забито 2 мяча или
меньше равна 0.262144+0.393216+0.24576 = 0.90112
Искомая вероятность (вероятность того, что будет забито
более двух мячей) равна 1–0.90112 = 0.09888 = 9.888%.
MX=np=6∙0.2 = 1.2
DX=np(1–p)= 6∙0.2∙0.8 = 0.96
11. Количество X принимаемых за час звонков по домашнему
телефону имеет распределение Пуассона. Среднее количество принимаемых за час
звонков – 6. Какова вероятность того, что будет принято 3 звонка? Более 2? Найти
математическое ожидание MX,
дисперсию DX.
Решение.
Найдем вероятность того, что будет принято 3 звонка.
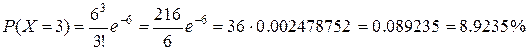
Найдем вероятность того, что будет принято более двух
звонков.
Дополнительным событием к искомому будет событие, что
принято 0,1 или 2 звонка. Найдем вероятность каждого из этих событий.
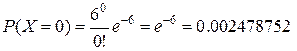
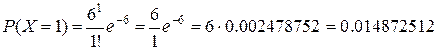
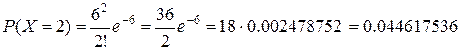
Получаем, вероятность того что будет принято 2 звонка или
меньше равна 0.002478752+0.014872512+0.044617536 = 0.0619688
Искомая вероятность (вероятность того, что будет принято
более двух звонков) равна 1–0.0619688 = 0.9380312 = 93.80312%.
12. Функция плотности случайной величины X имеет вид:
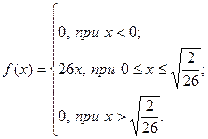
Найти математическое ожидание MX, дисперсию DX, P(0<X<0.1)
= 
= 
= 
= 
= 
= 
= 
= 
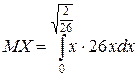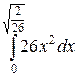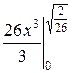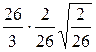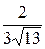
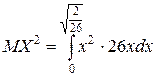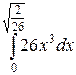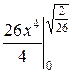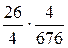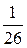
DX=MX2–(MX)2
= 
= 
= 
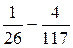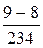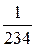
P(0<X<0.1)=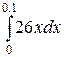 
= 
=
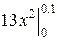13∙0.01 = 0.13
13. Случайная величина X – время ожидания дождя в сутках – имеет равномерное
распределение на отрезке [0,26]. Найти математическое ожидание MX, дисперсию DX, вероятности P(X<5),
P(X>3).
Решение.
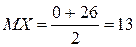
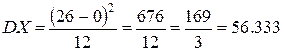
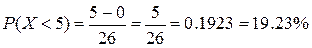
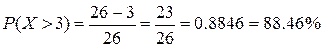
14. Вероятность безотказной работы прибора в течении x часов равна e–0.026x. Найти математическое
ожидание MX – среднюю
наработку на отказ и вероятность безотказной работы прибора в течение 100
часов.
Решение.
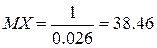
Вероятность безотказной работы прибора в течении 100 часов
равна
P(X>100)
= e-0.026∙100 = e-2.6 = 0.7427 = 74.27%
15. Случайная величина x имеет нормальное распределение
N(26;8). MX (математическое
ожидание X) = 26, среднеквадратическое
отклонение –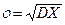 
= 8. Найти P(X<1),
P(–1<X<1), P(–5<x<5), P(–8<X–26<8) , P(–16<X–26<16) , P(–24<X–26<24).
Решение.
P(X<1) =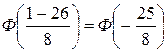 
= Ф(–3.125) = 0.0009
= 0.09%
P(–1<X<1) =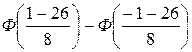 
= 
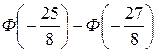= Ф(–3.125) – Ф(–3.175)
= 0.0009 – 0.00076 = 0.00014 = 0.014%
P(–5<X<5) = 
= 
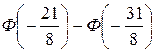= Ф(–2.625) – Ф(–3.875)
= 0.004335 – 0.000055 = 0.00428 = 0.428%
P(–8<X–26<8) = 2Ф(1) = 0.6826 =
68.26%
P(–16<X–26<16) = 2Ф(2) = 0.9544
= 95.44%
P(–24<X–26<24) = 2Ф(3) = 0.9973
= 99.73%
16. Вес мужчины – случайная величина со средним 80 кг и
дисперсией 15. Оценить с помощью неравенства Чебышева вероятность того, что вес
случайно встреченного мужчины отличается от среднего на величину, большую 11.
Решение.
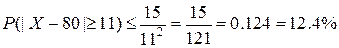
17. Вероятность детали быть бракованной равна 0.008.
Произведено 1000 деталей. Какова вероятность того, что в этой партии точно 2
бракованных детали? Более 2?
Решение.
λ = np
= 1000∙0.008 = 8
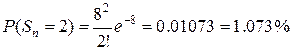
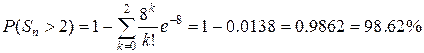
18. Игральную кость бросают 600 раз. Какова вероятность
того, что число выпадений шестерки будет между 86 и 111.
Решение.
Искомая вероятность будет равна
– 
= 
– 
= 
– 
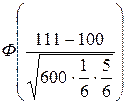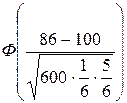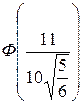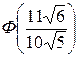= Ф(1.2) – Ф(–1.53) = 0.8849 – 0.063 = 0.8219 =
82.19%