1. Если множество 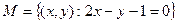 , то: а)
, то: а) 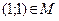 ; б)
; б) 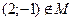 ; в)
; в) 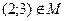 ; г)
; г) 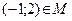 . Какие из вышеперечисленных высказываний истинны, а какие
ложны?
. Какие из вышеперечисленных высказываний истинны, а какие
ложны?
Решение.
а) 2∙1–1–1=0, следовательно, точка принадлежит
множеству и утверждение истинно.
б) 2∙2–(–1)–1≠0, следовательно, точка не
принадлежит множеству и утверждение истинно.
в) 2∙2–3–1=0, следовательно, точка принадлежит
множеству и утверждение ложно.
г) 2∙(–1)–2–1≠0, следовательно, точка не
принадлежит множеству и утверждение ложно.
2. Если N = {натуральные числа}, M = {положительные числа}, P = {простые
числа}, Q = {положительные
нечетные числа}, то истинны ли высказывания: а) 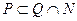 ; б)
; б) 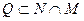 ; в)
; в) 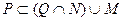 ; г)
; г) 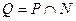 ?
?
Решение.
а) утверждение ложно, т.к. число 2 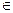 P и
P и 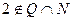 ;
;
б) утверждение истинно;
в) утверждение истинно;
г) утверждение ложно, т.к. нечетные составные числа принадлежат
Q и не принадлежат множеству в правой части равенства.
3. Найти область определения функции 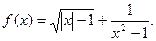
Решение.
Область определения функции – это множество множество точек
на числовой прямой, в которых имеет смысл каждое действие, указанное в формуле,
задающей функцию.
Т.к. в формулу входит радикал, то значение под ним не может
быть отрицательным, т.е. |x|–1≥0
или |x|≥1.
Т.к. в формулу входит дробь, то ее знаменатель не должен
обращаться в 0. Найдем точки, в которых знаменатель дроби обращается в 0.
x2–1=0
x2=1
x=–1;1
С учетом всего вышеизложенного получим область определения
функции.
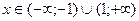
4. Из 220 школьников 163 играют в баскетболе, 175 – в
футбол, 24 не играют в эти игры. Сколько человек одновременно играют в
баскетбол и футбол?
Решение.
Найдем количество школьников, играющих или в баскетбол или в
футбол. Это количество равно 220–24=196 человек.
Число школьников, играющих одновременно в баскетбол и в
футбол равно 163+175–196=142 человека.
5. Пусть A – множество всех окружностей на плоскости и B –
множество всех точек на этой плоскости. Каждой окружности ставится в
соответствие ее центр. Является ли это соответствие взаимно однозначным?
Решение.
Это отображение не является взаимно однозначным, т.к. одна
точка является центром многих окружностей разного радиуса.
6. Правильно ли рассуждение, имеющее форму: «Все x являются
y и ни одно x не является z; значит, все y не являются z»?
Решение.
Это рассуждение неверно, т.к. в общем случае существует y,
которые не являются x и, соответственно могут быть z.
7. Проверить, что множество линейных функций вида y=ax+b,
где a и b – действительные числа, с операцией – сложением функций является
коммутативной группой.
Решение.
Проверим является ли это множество группой. Для этого
необходимо проверить три условия:
1) ассоциативность.
(((a1x+b1)+(a2x+b2))+(a3x+b3))=((a1x+b1)+((a2x+b2)+(a3x+b3)))
Это условие выполняется. Обе части равенства равны (a1+a2+a3)x+(b1+b2+b3)
2) Единичным элементом будет функция y=0.
(ax+b)+0=0+(ax+b)=ax+b
3) Обратным элементом для элемента (ax+b) будет элемент (–ax–b)
(ax+b)+(–ax–b)=(–ax–b)+(ax+b)=0.
Для того, чтобы данное множество являлось коммутативной
группой, необходимо выполнение условия коммутативности, т.е.
(a1x+b1)+(a2x+b2)=(a2x+b2)+(a1x+b1)
Это условие выполняется.