Задача 9.

На курсы иностранных языков зачислено 300 слушателей. Из них английский и немецкий изучают 60 человек, английский и французский – 70 человек. Число слушателей, изучающих только французский язык, равно числу слушателей, изучающих только немецкий язык. Только английский язык изучают 60 слушателей. Только немецкий язык изучает число слушателей на 10 меньше, чем число слушателей, изучающих только английский и немецкий языки. Занятия по французскому и немецкому языкам проводятся единовременно. Сколько слушателей не посещают занятия?

Решение.

Обозначим через

М_В – количество всех  слушателей, посещающих занятия;

М_А – количество слушателей, изучающих только английский язык;

М_Н – количество слушателей, изучающих только немецкий язык;

М_Ф – количество слушателей, изучающих только французский язык;

М_АН – количество слушателей, изучающих только английский и немецкий языки;

М_АФ – количество слушателей, изучающих только английский и французский языки;

 М_НФ – количество слушателей, изучающих только немецкий и французский языки;

 М_АНФ – количество слушателей, изучающих три языка.

Диаграмма Эйлера-Вена:

 

По условию задачи,  так как английский и немецкий языки изучают 60 человек, получаем:

М_АН + М_АНФ = 60   (условие 1).

Так как английский и французский языки изучают 70 человек, получаем:

М_АФ + М_АНФ = 70   (условие 2).

Так как число слушателей, изучающих только французский язык, равно числу слушателей, изучающих только немецкий язык, то

М_Ф = М_Н     (условие 3).

Так как только английский язык изучают 60 слушателей, то

М_А= 60        (условие 4).

Так как только немецкий язык изучает число слушателей на 10 меньше, чем число слушателей, изучающих только английский и немецкий языки, то

М_Н = М_АН – 10   (условие 5).

Так как занятия по французскому и немецкому языкам проводятся единовременно, т.е. нельзя изучать французский и немецкий язык, то

М_НФ + М_АНФ = 0    (условие 6).

Требуется   найти  300 – М_В.

Из условия 6 получаем М_НФ = М_АНФ = 0 .

Тогда из условий  1 и 2: М_АН  = 60,   М_АФ = 70   .

Следовательно, по условию 5: М_Н = 60 – 10 = 50.

Тогда по условию 3: М_Ф = М_Н = 50.

Из диаграммы Эйлера-Вена получаем: М_В = М_А + М_Н + М_Ф + М_АН + М_АФ + М_НФ + М_АНФ=60+50+50+60+70+0+0=290.

Получаем: 300 – М_В = 300-290 =10.

Ответ: 10 слушателей не посещают занятия.

Задача 19.

Галя и Борис – ровесники или Галя старше Бориса. Если Галя и Борис – ровесники, то Оля и Борис – разного возраста. Если Галя старше Бориса, то Борис старше Коли. Следовательно, Оля и Борис – разного возраста или Борис старше Коли.

Решение.

Обозначим высказывания:

А – «Галя и Борис – ровесники»;

В – «Галя старше Бориса»;

С – «Оля и Борис – разного возраста»;

D – «Борис старше Коли».

Данное рассуждение можно представить в виде формулы:

.

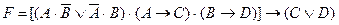Проверим формулу на тождественную истинность.

Введем обозначение: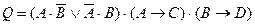

Составляем таблицу истинности:

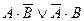
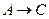
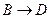
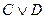
А	B	C	D				Q		F
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА
ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА
ЛОЖЬ	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА
ЛОЖЬ	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ИСТИНА
ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ИСТИНА
ЛОЖЬ	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
ИСТИНА	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА
ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА
ИСТИНА	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ИСТИНА
ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА
ИСТИНА	ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ИСТИНА
ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА

Так  как формула F   является тождественно истинной, данное рассуждение  верно. Задача 29.

По заданной функции проводимости построить СКНФ и СДНФ. Упростить полученные формулы:

.

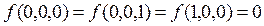Решение.

Исходя из условия, построим таблицу истинности заданной функции проводимости:

х	y	z	f(x,y,z)
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

По наборам, на которых функция равна 1, строим СДНФ:

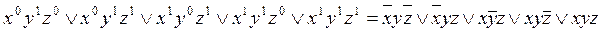
По наборам, на которых функция равна 0, строим СКНФ:

.

Упростим СДНФ:

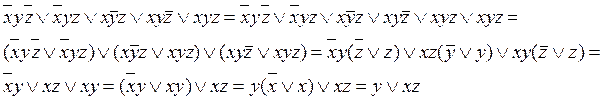
Упростим СКНФ:

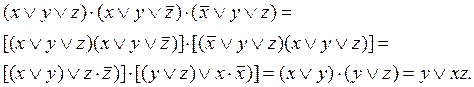
Для проверки равносильности формул составим таблицу истинности формулы :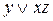

х	y	z
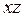
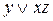
0	0	0	0	0
0	0	1	0	0
0	1	0	0	1
0	1	1	0	1
1	0	0	0	0
1	0	1	1	1
1	1	0	0	1
1	1	1	1	1

Так как таблицы истинности для f(x,y,z) и 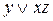 совпадают, формулы эквивалентны.

Литература.

1.                Информатика. Учебник/ Под ред. проф. Н.В.Макаровой. – М.: Финансы статистика, 1997.

2.                Информатика и математика и для юристов: Учеб. пособие  для вузов/ Под ред. проф. Х.А.Андриашина, проф. С.Я. Казанцева. – М.: ЮНИТИ-ДАНА, Закон и право, 2001.

3.                Богатов Д.Ф., Богатов Ф.Г. Основы информатики и математики для юристов: Учеб. пособие. В 2-х томах. М.: ПРИОР, 2000.