ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ




Кафедра Бухгалтерского учета, аудита и статистики



О Т Ч Е Т

о результатах выполнения

компьютерной лабораторной работы №1



«Автоматизированный априорный анализ статистической совокупности в среде MS Excel»


Вариант № 3



















Уфа, 2007 г.

Постановка задачи

При проведении статистического наблюдения за деятельностью предприятий корпорации получены выборочные данные по 32-м предприятиям, выпускающим однородную продукцию  (выборка 10%-ная, механическая), о среднегодовой стоимости основных производственных фондов и  о выпуске продукции за год.

В проводимом статистическом исследовании обследованные предприятия выступают как единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые признаки единиц.

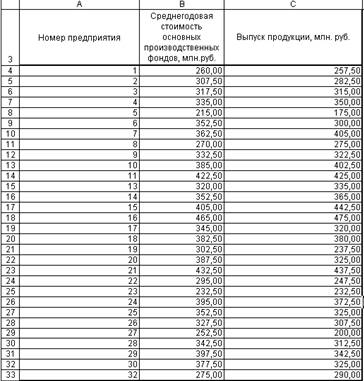
Для проведения автоматизированного статистического анализа совокупности выборочные данные представлены в формате электронных таблиц процессора Excel в диапазоне ячеек B4:C35. Для демонстрационного примера (ДП) выборочные данные приведены в табл. 1-ДП.

Таблица 1-ДП

Исходные данные примера

В процессе исследования совокупности необходимо решить ряд статистических задач для выборочной и генеральной совокупностей.

 

Статистический анализ выборочной совокупности

1.     Выявить наличие среди исходных данных резко выделяющихся значений признаков («выбросов» данных) с целью исключения из выборки аномальных единиц наблюдения.

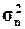2.     Рассчитать обобщающие статистические показатели совокупности по изучаемым признакам: среднюю арифметическую (), моду (Мо), медиану (Ме), размах вариации (R), дисперсию(), средние отклонения – линейное (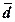) и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент асимметрии  К.Пирсона (Asп).

3.     На основе рассчитанных показателей в предположении, что распределения единиц по обоим признакам близки к нормальному, оценить:

а) степень колеблемости значений признаков в совокупности;

б) степень однородности совокупности по изучаемым признакам;

в) устойчивость индивидуальных значений признаков;

г) количество попаданий индивидуальных значений признаков в диапазоны (), (), ().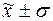

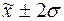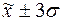4.     Дать сравнительную характеристику распределений единиц совокупности по двум изучаемым признакам на основе анализа:

а) вариации признаков;

б) количественной однородности единиц;

в) надежности (типичности) средних значений признаков;

г) симметричности распределений в центральной части ряда.

5.     Построить интервальный вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и установить характер (тип) этого распределения. Рассчитать моду Мо полученного интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.


Статистический анализ  генеральной совокупности

1.                Рассчитать генеральную дисперсию 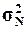, генеральное среднее квадратическое отклонение 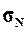 и ожидаемый размах вариации признаков RN. Сопоставить значения этих показателей для генеральной и выборочной дисперсий.

2.                Для изучаемых признаков рассчитать:

а) среднюю ошибку выборки;

б) предельные ошибки выборки для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут находиться средние значения признака генеральной совокупности при заданных уровнях надежности.

3.                Рассчитать коэффициенты асимметрии As и эксцесса Ek. На основе полученных оценок  сделать вывод о степени близости распределения единиц генеральной совокупности к нормальному распределению.


1.               Подготовительный этап


На данном этапе  необходимо проделать следующие обязательные действия, связанные с организацией индивидуальной рабочей среды:

·              запустить Excel и подготовить персональную папку с рабочим и отчетным файлами;

·              сформировать индивидуальный вариант исходных данных и записать его в отчетный файл;

·              проверить наличие в Excel  надстройки Пакет анализа;

·              проверить установку форматов чисел на компьютере.


1.                Запуск Excel и подготовка персональной папки студента  с рабочим и отчетным файлами


Для выполнения расчетов обобщающих показателей и подготовки отчета по лабораторной работе нужно сформировать персональную папку с именем ФИО, содержащую два файла: расчетный с именем Лаб1. хls и отчетный с именем Отчет1.doc.

Для создания рабочего файла проделать следующие действия:

1.           Загрузить файл с исходными данными и макетами таблиц по следующему алгоритму:

·                   На рабочем столе активизировать Мой компьютер;

·                   В диалоговом окне выбрать файл Datadisk на “primary” (E:)\Преподаватели\Кафедра статистики\Априорный анализ\ stat_lab.xls.

2.           Сохранить файл с исходными данными в качестве рабочего файла по алгоритму:

·                   Файл=>Сохранить как…;

·                   В диалоговом окне Сохранение документа выбрать путь: Datadisk на “primary” (Е:)\Статистика\ Работы студентов\<Специальности>\ <Номер группы>\<Ф.И.О.>;

·                   Сохранить файл в указанной папке под именем Лаб1. хls.

Для создания отчетного файла проделать следующие действия:

1.           Загрузить файл Формат отчета.doc из директории Datadisk на “primary” (E:)\Преподаватели\Кафедра статистики \Априорный анализ.

2.           Сохранить файл по алгоритму:

·                   Файл=>Сохранить как…;

·                   В диалоговом окне Сохранение документа выбрать путь: Datadisk на “primary” (Е:)\Статистика\ Работы студентов\<Специальности>\ <Номер группы>\<Ф.И.О.>;

·                   Сохранить файл в указанной папке под именем Отчет1.doc.

2.                Формирование индивидуальных исходных данных и запись их в отчетный файл


Для того, чтобы сформировать индивидуальные исходные данные, необходимо ввести номер варианта в ячейку E2 созданного рабочего файла Лаб1. хls, в результате чего Excel сформирует исходные данные варианта.

Для записи исходных данных варианта в отчетный файл Отчет1.doc необходимо скопировать сформированную табл. 1 из рабочего файла в файл Отчет1.doc в выделенное для этой цели место.


3.                Проверка наличия в Excel надстройки ПАКЕТ АНАЛИЗА


Для выполнения лабораторной работы необходимо наличие в Excel программной настройки Пакет анализа.

В случае если Пакет анализа установлен, то меню Сервис будет содержать пункт подменю Анализ данных. Если же этот пункт в меню Сервис отсутствует, необходимо активизировать инструмент Пакет анализа действиями:

1.                Сервис=>Надстройки;

2.                В диалоговом окне Надстройки отметить пункт Пакет анализа;

3.                ОК.

4.                Установка форматов чисел на компьютере

Перед началом работы следует убедиться, что компьютер настроен на формат дробных чисел и разделителей, применяемый в алгоритмах лабораторной работы, а именно:

·              дробная часть числа должна отделяться от целой части знаком «запятая» (,);

·              аргументы функций (разделители списков) должны отделяться знаком «точка с запятой» (;).

Иная настройка форматов чисел на компьютере (например, дробная часть отделяется от целой знаком  «точка» (.) или же аргументы функции (разделители списков) перечисляются через запятую) будет приводить к ошибкам при вводе в электронные таблицы Excel формул, указанных в алгоритмах Задания 2.

Установить в компьютере совместимый с текстами алгоритмов формат чисел можно следующим образом:

1.                Пуск=>Настройка=>Панель управления=>Язык и стандарты;

2.                Язык и стандарты=>Числа;

3.                В поле Разделитель целой и дробной части ввести символ «,»;

4.                В поле Разделитель элементов списка ввести символ «;».

2. Этап выполнения статистических расчетов

 

Задание 1 Выявление и удаление из выборки аномальных единиц наблюдения

Первичные данные выборочной совокупности могут содержать аномальные значения изучаемых признаков. Задание 1 заключается в их выявлении и исключении из дальнейшего рассмотрения с целью обеспечения устойчивости данных статистического анализа.


Алгоритм выполнения Задания 1


Этап 1. Построение диаграммы рассеяния изучаемых признаков


1.                Выделить мышью оба столбца исходных данных в диапазоне B4:C35.

2.                Вставка=>Диаграмма=>Точечная=>Готово.

В результате выполнения этих действий на рабочем листе Excel появится диаграмма рассеяния (рис. 1).


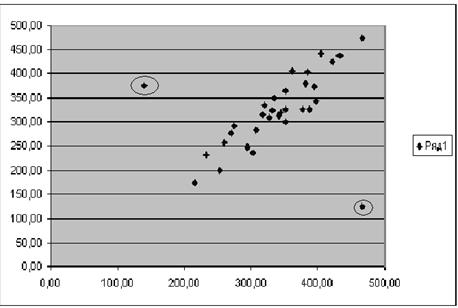
Рис. 1. Аномальные значения признаков на диаграмме рассеяния.

Этап 2. Визуальный анализ диаграммы рассеяния, выявление и фиксация аномальных значений признаков, их удаление из первичных данных

1.                Найти на графике точку, соответствующую аномальному наблюдению. Если таких точек нет, то перейти к действию 7, если есть - к действиям 2 - 6.

2.                Подвести курсор к точке на диаграмме рассеяния, соответствующей аномальному наблюдению. После непродолжительного времени возле точки автоматически появится надпись, содержащая значения признаков этого наблюдения в формате (X,Y).

Для исходного примера такая надпись выглядит следующим образом:


Рис. 2


3.                В исходных данных визуально (либо с помощью поисковых средств Excel) найти в табл.1 строку, соответствующую выявленной  аномальной единице наблюдения (предприятию). Скопировать эту строку в табл.2.

4.                Выделить мышью всю адресную строку с данными, подлежащими удалению.

Для удаления из исходных данных табл. 1 строк с аномальными данными необходимо выделить мышью соответствующую адресную строку вместе с ее номером!

         Для исходного примера это предприятия с номером 12 и 31.

5.                Правка => Удалить.

6.                Выполнять действия 1-5 до полного удаления всех аномальных наблюдений.

7.                Переместить диаграмму рассеяния в область ячеек, начиная с ячейки F4.

Для исходного примера табл.2 имеет следующий вид.

Таблица 2-ДП

Аномальные единицы наблюдения

Номер предприятия

Среднегодовая стоимость основных производственных фондов, млн.руб.

Выпуск продукции, млн. руб.

12

50,00

150,00

31

30,00

53,00

Задание 2 Оценка описательных статистических параметров совокупности

Обобщающие статистические показатели совокупности исчисляются на основе анализа вариационных рядов распределения. Однако пакет Excel позволяет рассчитать многие из этих показателей непосредственно по первичным данным наблюдения, используя инструмент Описательная статистика надстройки Пакет анализа,  а также статистические функции инструмента Мастер функций.

Выполнение Задания 2 заключается в автоматизированном решении двух статистических задач:

1.           Расчет описательных показателей выборочной и генеральной совокупностей по несгруппированным выборочным данным с использованием инструментов Описательная статистика и Мастер функций.

2.           Оценка средней и предельной ошибок выборки для средней величины признака, а также границ, в которых эта средняя будет находиться в генеральной совокупности при заданных уровнях надежности.

Алгоритмы выполнения Задания 2


Выполнение задания включает три этапа:

1.           Расчет описательных параметров выборочной и генеральной совокупностей с использованием инструмента Описательная статистика.

2.           Оценка предельных ошибок выборки для различных уровней надежности в режиме Описательная статистика.

3.           Расчет описательных параметров выборочной совокупности с использованием инструмента Мастер функций.

Этап 1. Расчет описательных параметров выборочной и генеральной совокупностей с использованием инструмента ОПИСАТЕЛЬНАЯ СТАТИСТИКА

Алгоритм 1.1. Расчет описательных статистик

1.           Сервис =>Анализ данных =>Описательная статистика =>OK;

2.           Входной интервал<= диапазон ячеек таблицы, выделенный согласно табл. 3-М для значений признаков Стоимость основных фондов и Выпуск продукции;

3.           Группирование =>по столбцам;

4.           Итоговая статистика - Активизировать;

5.           Уровень надежности - Активизировать;

6.           Уровень надежности <= 95,4;

7.           Выходной интервал <= адрес  ячейки  заголовка  первого  столбца  табл.3;

8.           OK;

9.           При появлении окна с сообщением "Выходной интервал накладывается на имеющиеся данные" =>ОК.

В результате указанных действий Excel осуществляет вывод таблицы описательных статистик в заданный диапазон рабочего файла (таб.3).


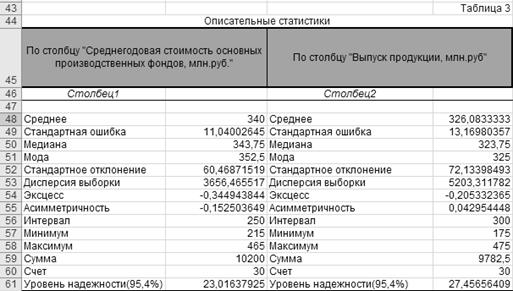
Этап 2. Оценка предельных ошибок выборки для различных уровней надежности в режиме Описательная статистика.


Алгоритм 2.1. Расчет предельной ошибки выборки при P=0,683

1.                Сервис =>Анализ данных =>Описательная статистика =>OK;

2.                Входной интервал<= диапазон ячеек таблицы, выделенный согласно табл. 3-М для значений признаков Стоимость основных фондов и Выпуск продукции;

3.                Итоговая статистика – Снять флажок;

4.                Уровень надежности – Активизировать;

5.                Уровень надежности<=  68,3;

6.                Выходной интервал <= адрес ячейки, выделенной согласно табл. 3-М для предельной ошибки выборки при P=0,683;

7.                OK;

8.                При появлении окна с сообщением "Выходной интервал накладывается на имеющиеся данные" =>ОК.

Алгоритм 2.2. Расчет предельной ошибки выборки при P=0,997

1.                Сервис=>Анализ данных=>Описательная статистика=>OK;

2.                Входной интервал<= диапазон ячеек таблицы, выделенный согласно табл. 3-М для значений признаков Стоимость основных фондов и Выпуск продукции после удаления аномальных значений;

3.                Итоговая статистика –  Снять флажок;

4.                Уровень надежности – Активизировать;

5.                Уровень надежности <= 99,7;

6.                Выходной интервал <= адрес ячейки, выделенный согласно табл.3-М для предельной ошибки выборки при P=0,997;

7.                OK;

8.                При появлении окна с сообщением "Выходной интервал накладывается на имеющиеся данные" =>ОК.

В результате работы алгоритмов 2.1 и 2.2 Excel выводит в соответствующие ячейки табл.4 рабочего файла значения предельных ошибок выборки при P=0,683 и P=0,997 (табл.4а и табл.4б).



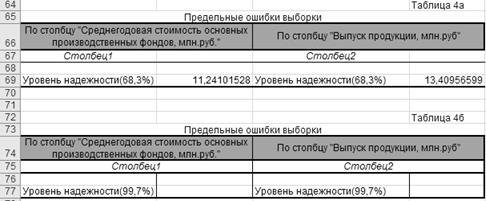
Этап 3. Расчет описательных параметров выборочной совокупности с использованием инструмента Мастер функций


Алгоритм 3.1. Расчет выборочного стандартного отклонения σn для признака Среднегодовая стоимость основных производственных фондов

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для среднего квадратического отклонения первого признака;

2.                Вставка=>Функция;

3.                Статистические=>СТАНДОТКЛОНП=>ОК;

4.                Число 1<=диапазон ячеек табл.1, содержащих значения первого признака.


Алгоритм 3.2. Расчет выборочного стандартного отклонения σn для признака Выпуск продукции

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для среднего квадратического отклонения второго признака;

2.                Вставка=>Функция;

3.                Статистические=>СТАНДОТКЛОНП=>ОК;

4.                Число 1<=диапазон ячеек табл.1, содержащих значения второго признака.


Алгоритм 3.3. Расчет выборочной дисперсии σ2n для признака Среднегодовая стоимость основных производственных фондов

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для выборочной дисперсии первого признака;

2.                Вставка=>Функция;

3.                Статистические=>ДИСПР=>ОК;

4.                Число1<= диапазон ячеек табл.1, содержащий значения первого признака.


Алгоритм 3.4. Расчет выборочной дисперсии σ2n по признаку Выпуск продукции

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для выборочной дисперсии второго признака;

2.                Вставка=>Функция;

3.                Статистические=> ДИСПР=>ОК;

4.                Число1<= диапазон ячеек табл.1, содержащих значения второго признака.

Алгоритм 3.5. Расчет выборочного среднего линейного отклонения 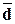 по признаку Среднегодовая стоимость основных производственных фондов

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для среднего линейного отклонения первого признака;

2.                Вставка=>Функция;

3.                Статистические=>СРОТКЛ=>ОК;

4.                Число1<= диапазон ячеек табл.1, содержащих значения первого признака.


Алгоритм 3.6. Расчет выборочного среднего линейного отклонения 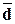 по признаку Выпуск продукции

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для среднего линейного отклонения второго признака;

2.                Вставка=>Функция;

3.                Статистические=> СРОТКЛ =>ОК;

4.                Число1<= диапазон ячеек табл.1, содержащих значения второго признака.


Алгоритм 3.7. Расчет коэффициента вариации 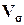 по признаку Среднегодовая стоимость основных производственных фондов

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для коэффициента вариации первого признака;

2.                В активизированную ячейку ввести формулу =B83/B48*100.


Алгоритм 3.8. Расчет коэффициента вариации 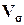 по признаку Выпуск продукции

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для коэффициента вариации второго признака;

2.                В активизированную ячейку ввести формулу =D83/D48*100.


Алгоритм 3.9. Расчет выборочного коэффициента асимметрии Пирсона Asп по признаку Среднегодовая стоимость основных производственных фондов

1.                Установить курсор в ячейку, выделенную согласно табл.3-М для коэффициента асимметрии первого признака;

2.                В активизированную ячейку ввести формулу =(B48-B51)/B83.

Алгоритм 3.10. Расчет выборочного коэффициента асимметрии Пирсона Asп по признаку Выпуск продукции

1.                Установить курсор в ячейку, выделенную согласно табл.3 для коэффициента асимметрии второго признака;

2.                В активизированную ячейку ввести формулу =(D48-D51)/D83.

В результате работы алгоритмов 3.1 - 3.10 Excel осуществляет вывод значений выборочных параметров σn, σ2n, 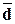,  и Аsn в соответствующие ячейки рабочего листа (табл.5).





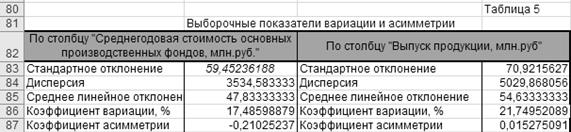
Задание 3 Построение и графическое изображение интервального вариационного ряда распределения единиц совокупности по признаку  Среднегодовая стоимость основных производственных фондов

Для того, чтобы выявить структуру совокупности и тип закономерности распределения ее единиц по варьирующему признаку, строят и анализируют интервальный  вариационный  ряд  распределения  и его гистограмму (см. п. 3 раздела II – Теоретические основы лабораторной работы).

Выполнение Задания 3 заключается в решении двух статистических задач:

1.           Построение интервального ряда распределения единиц выборочной совокупности по признаку Среднегодовая стоимость основных производственных фондов.

2.           Построение гистограммы и кумуляты сформированного интервального ряда.


Алгоритмы выполнения Задания 3


Выполнение задания осуществляется в три этапа:

1.                Построение промежуточной таблицы.

2.                Генерация выходной таблицы и графиков.

3.                Приведение выходной таблицы и диаграммы к виду, принятому в статистике.


Этап 1. Построение промежуточной таблицы.

Алгоритм 1.1. Расчет нижних границ интервалов

1.                Сервис=>Анализ данных=>Гистограмма=>ОК;

2.                Входной интервал<= диапазон ячеек, выделенный согласно табл. 5-М для столбца значений первого признака;

3.                Интервал карманов оставить незаполненным;

4.                Выходной интервал <= адрес заголовка первого столбца первичной промежуточной табл.6 (см. табл.5-М).

5.                OK.


Алгоритм 1.2.  Переход от нижних границ к верхним

1.                Выделить курсором верхнюю левую ячейку табл.6 и нажать клавишу [Delete];

2.                Ввести в ячейку с именем "Еще" значение хmax первого признака из табл.3-Описательные статистики.

Для исходного примера построение промежуточной таблицы (алгоритмы 1.1 – 1.2) приведено на рис.11:


                                          

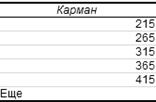
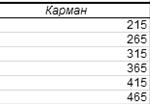
Рис.4. Схема перехода от нижних границ интервалов к верхним


Этап 2. Генерация выходной таблицы и графиков

Алгоритм 2.1. Построение выходной таблицы, столбиковой диаграммы и кумуляты.

1.                Сервис=>Анализ данных=>Гистограмма=>ОК;

2.                Входной интервал<= диапазон ячеек, выделенный согласно табл. 5-М для столбца значений первого признака;

3.                Интервал карманов <= диапазон карманов итоговой промежуточной табл.6 с верхними границами (см. табл.5-М);

4.                Выходной интервал <= адрес заголовка первого столбца выходной  табл.7 (см. табл.5-М);

5.                Интегральный процент - Активизировать;

6.                Вывод графика  - Активизировать;

7.                ОК;

8.                При появлении сообщения о наложении данных  - ОК.

Для исходного примера выходная таблица имеет следующий вид:



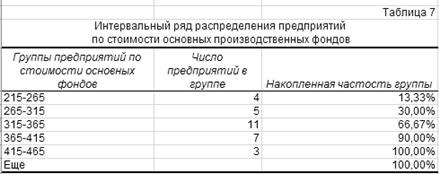
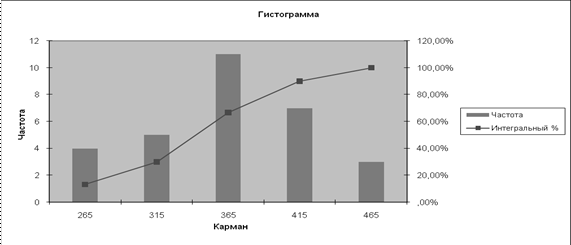
Столбиковая диаграмма и кумулята приведены ниже:




Этап 3. Приведение выходной таблицы и диаграммы к виду, принятому в статистике.

Алгоритм 3.1. Преобразование выходной таблицы в результативную.

1.           Заменить названия столбцов выходной табл.7 в соответствии с табл.6-М;

2.           Строки первого столбца привести к виду «нижняя граница интервала  -  верхняя граница интервала», учитывая совпадение верхних границ предыдущего интервала с нижней границей последующего интервала;

3.           Строку с именем «Еще» выделить мышью и очистить, нажав  клавишу [Delete];

4.           Добавить и заполнить строку с именем «Итого».


Таблица 6-М

Название столбца в выходной таблице

Название столбца в результативной таблице

Карман

Группы предприятий по стоимости основных фондов

Частота

Число предприятий в группе

Интегральный %

Накопленная частость группы

Для нашего примера Excel-формат результативной таблицы выглядит следующим образом.



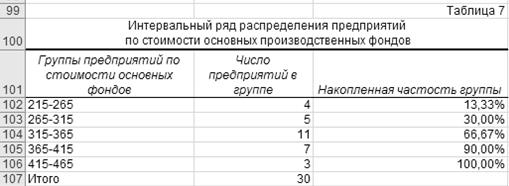
Алгоритм 3.2. Преобразование столбиковой диаграммы в гистограмму.

1.                Осуществив «захват мышью», переместить график, расположив его вслед за табл.7 согласно адресации, указанной в табл.5-М;

2.                Исключить зазоры, выполнив следующие  действия:

2.1. Нажать правую кнопку мыши на одном из столбиков диаграммы.;

2.2. Формат рядов данных=>Параметры;

2.3. Ширина зазора<= 0;

2.4. ОК;

3.                Используя "захват мышью" за угол поля графика, установить соотношение  ширины  и  высоты фигуры гистограммы в пропорции 1 : 0,62.

Для исходного примера гистограмма и кумулята выглядят следующим образом


 



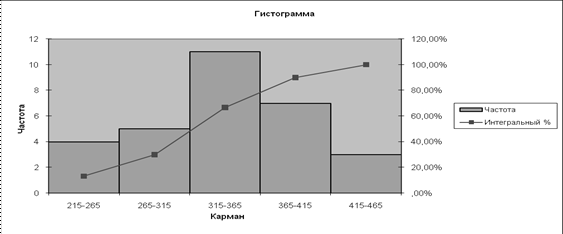
Вывод: сделав данную лабораторную работу, я научилась с помощью пакета анализа данных анализировать статистические данные, рассчитывать показатели и строить на основании полученных данных график ряда распределения (гистограмму и кумуляту).