Содержание


Введение.. 3

1. Функциональные зависимости для временных рядов (рядов динамики) 5

2. Статистические (корреляционные) зависимости в общем случае   8

3. Линейная корреляция в общем случае.. 9

3.1 Парный линейный коэффициент корреляции. 9

3.2 Понятие о коэффициенте детерминации. 10

4. Линейная регрессия в общем случае.. 10

4.1 Суть метода наименьших квадратов. 10

4.2 Интерпретация коэффициента регрессии. 12

4.3 Коэффициент детерминации. 12

5. Нелинейная регрессия и нелинейная корреляция в общем случае   14

5.1 Построение уравнений нелинейной регрессии. 14

5.2 Измерение тесноты связи при криволинейной зависимости. 16

6. Аналитическое выравнивание ряда динамики.. 18

Заключение.. 19

Литература.. 23

 

Введение

Анализ взаимосвязей, присущих изучаемым процессам и явлениям, является важнейшей задачей статистических исследований. В тех случаях, когда речь идет о явлениях и процессах, обладающих сложной структурой и многообразием свойственных им связей, такой анализ представляет собой сложную задачу. Прежде всего необходимо установить наличие взаимосвязей и их характер. Вслед за этим возникает вопрос о тесноте взаимосвязей и степени воздействия различных факторов (причин) на интересующий исследователя результат. Если черты и свойства изучаемых объектов могут быть измерены и выражены количественно, то анализ взаимосвязей может вестись на основе применения математических методов. Использование этих методов позволяет проверить гипотезу о наличии или отсутствии взаимосвязей между теми или иными признаками, выдвигаемую на основе содержательного анализа. Далее, лишь посредством математических методов можно установить тесноту и характер взаимосвязей или выявить силу (степень) воздействия различных факторов на результат.

Наиболее разработанными в математической статистике методами анализа взаимосвязей являются корреляционный и регрессионный анализ.

Анализ статистической, или корреляционной, связи предполагает выявление формы связи, а также оценку тесноты связи. Первая задача решается методами регрессионного анализа, вторая — методами корреляционного анализа. Регрессионный анализ сводится к описанию статистической связи с помощью подходящей функциональной зависимости. Корреляционный анализ позволяет оценивать тесноту связи посредством специальных показателей, причем выбор их зависит от вида функциональной зависимости, пригодной для адекватного описания рассматриваемой статистической взаимосвязи. [1]

Тенденцию ряда динамики представляют в виде гладкой кривой (траектории), которая аналитически выражается некоторой функцией времени, называемой трендом.

Тренд характеризует основную закономерность движения во времени, свободную в основном (но не полностью) от случайных воздействий.

Уровни временного ряда описывают следующим уравнением тренда:

где  — систематическая составляющая, характеризующая основную тенденцию;

 — случайная составляющая.

1. Функциональные зависимости для временных рядов (рядов динамики)

Функциональная зависимость двух количественных признаков или переменных состоит в том, что каждому значению одной переменной всегда соответствует одно определенное значение другой переменной. Если исследуемый признак зависит от времени, то имеем дело с рядом динамики как с частным случаем функциональной зависимости.

Отметим наиболее употребительные формы функциональной зависимости, применяемые при исследовании рядов динамики.

Линейная:

,

где  — уровни, освобожденные от колебаний, выровненные по прямой;

b — начальный уровень тренда в момент или период, принятый за начало отсчета времени;

а — среднегодовой абсолютный прирост (среднее изменение за единицу времени t).

Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям. Равнодействующая этих факторов при взаимном погашении особенностей отдельных факторов (ускорение, замедление, не-линейность) часто выражается в примерно постоянной абсолютной скорости изменения, т.е. в прямолинейном тренде.

Графическим изображением линейной зависимости служит прямая линия.

Линейная зависимость является наиболее простой и в определенном смысле универсальной формой связи многих явлений. Ее универсальность состоит в том, что более сложные зависимости часто можно рассматривать «в первом приближении» как линейные.


Параболическая форма тренда:

где с — квадратический параметр, равный половине ускорения.

 Параболическая форма тренда выражает ускоренное или замедленное изменение уровней ряда с постоянным ускорением. Такой характер развития можно ожидать при наличии важных факторов прогрессивного (регрессивного) развития.

 Экспоненциальная форма тренда:

,

где k — темп изменения в разах; константа тренда.

Если k >1, экспоненциальный тренд выражает тенденцию ускоренного и все более ускоряющегося возрастания уровней.

При росте по экспоненте абсолютный прирост пропорционален достигнутому уровню. Так росло население Земли в эпоху «демографического взрыва» в XX столетии.

При k <1 экспоненциальный тренд означает тенденцию постоянно все более замедляющегося роста уровней динамического ряда.

 

Логарифмическая форма тренда:

Логарифмический тренд пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельного возможного значения.

Непосредственно функциональные зависимости в чистом виде редко встречаются в общественных явлениях. Связи обычно носят гораздо более сложный характер. Однако их описание во всей сложности часто затруднительно, да и нецелесообразно. Поэтому их рассматривают как соответствующие тем или иным видам функциональной зависимости. Простейшей формой функциональной связи является линейная зависимость, которая широко используется в регрессионном и особенно в корреляционном анализе. Гипотеза о линейной связи между исследуемыми признаками получила широкое распространение в анализе взаимосвязей. Лишь в том случае, если результаты применения гипотезы о линейной зависимости оказываются неудачными или имеются веские основания против линейной связи, используют более сложные функциональные зависимости.

Подбор подходящей функциональной зависимости на основе графического и логического анализа является важным этапом исследования взаимосвязей, особенно в тех случаях, когда линейная связь оказалась неприемлемой.

2. Статистические (корреляционные) зависимости в общем случае

Функциональная зависимость между признаками предполагает их изолированность, она действует, так сказать, «при прочих равных условиях». В общественной жизни такие ситуации бывают крайне редко. Как правило, воздействие одной переменной (причины) на другую не изолировано от остальных факторов, а происходит, таким образом, что на изучаемую связь прямо или косвенно влияют многие другие факторы. Здесь налицо зависимость особого вида. Для описания и изучения такого рода зависимостей в науке используется понятие статистический, или корреляционной, связи.[2]

В отличие от функциональной зависимости, когда каждому значению одного признака всегда соответствует определенное значение другого, при статистической зависимости одному и тому же значению одного признака могут соответствовать различные значения другого. Это происходит в силу того, что при статистической зависимости связь устанавливается между признаками (двумя, тремя и т. д.), которые изменяются не только в силу взаимодействия между собой, но и под воздействием множества различных неучтенных факторов. В результате множественного воздействия взаимно переплетающихся факторов связь между признаками существует и проявляется не в каждом отдельном случае, как при функциональной связи, а только в тенденции, «в среднем». Поэтому здесь установить наличие взаимосвязи и определить ее количественную меру можно не на основе единичных наблюдений, а лишь применительно к определенной совокупности объектов, т. е. в среднем по отношению к тем или иным массовым объектам или явлениям. Характеризующие эти объекты количественные показатели в источниковедении и в статистике называются массовыми данными.

3. Линейная корреляция в общем случае

Одной из основных мер связи в корреляционном анализе является линейный коэффициент корреляции.

3.1 Парный линейный коэффициент корреляции

С помощью парного линейного коэффициента корреляции измеряется теснота связи между двумя признаками. Линейный коэффициент корреляции чаще всего рассчитывается по формуле:

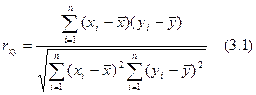
где xi и yi — значения признаков х и у соответственно для i-ro объекта, i=1, .., n; n — число объектов;  и — средние арифметические значения признаков х и у соответственно.[3]

Линейный коэффициент корреляции изменяется в пределах от —1 до +1. Равенство коэффициента нулю свидетельствует об отсутствии линейной связи. Равенство коэффициента —1 или +1 показывает наличие функциональной связи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «–» — на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).

Линейный коэффициент корреляции является показателем взаимной связи между признаками и не дает представления о том, какой из признаков является факторным, а какой — результативным (в формуле (3.1) признаки х и у совершенно равноправны).

3.2 Понятие о коэффициенте детерминации

Линейный коэффициент корреляции оценивает тесноту взаимосвязи между признаками и показывает, является ли связь прямой или обратной. Но понятие тесноты взаимосвязи часто может быть недостаточным при содержательном анализе взаимосвязей. В частности, коэффициент корреляции не показывает степень воздействия факторного признака на результативный. Таким показателем является коэффициент детерминации (обозначим его D), для случая линейной связи представляющий собой квадрат парного линейного коэффициента корреляции (D=r2) или квадрат множественного коэффициента корреляции. Его значение определяет долю (в процентах) изменений, обусловленных влиянием факторного признака, в общей изменчивости результативного признака.

4. Линейная регрессия в общем случае

Регрессионный анализ позволяет приближенно определить форму связи между результативным и факторными признаками, а также решить вопрос о том, значима ли эта связь. Вид функции, с помощью которой приближенно выражается форма связи, выбирают заранее, исходя из содержательных соображений или визуального анализа данных. Математическое решение задачи основано на методе наименьших квадратов.

4.1 Суть метода наименьших квадратов

Пусть имеются данные о значениях результативного признака у, соответствующие некоторым значениям  факторного признака х. Попытаемся представить интересующую нас зависимость с помощью прямой линии. Разумеется, такая линия может дать только приближенное представление о форме реальной статистической связи. Постараемся сделать это приближение наилучшим. Оно будет тем лучше, чем меньше исходные данные будут отличаться от соответствующих точек, лежащих на линии. Степень близости может быть выражена величиной суммы квадратов отклонении, реальных значений от расположенных на прямой. Использование квадратов отклонений позволяет суммировать отклонения различных знаков без их взаимного погашения и дополнительно обеспечивает сравнительно большее внимание, уделяемое большим отклонениям. Именно этот критерий (минимизация суммы квадратов отклонений) положен в основу метода наименьших квадратов.

В вычислительном аспекте метод наименьших квадратов сводится к составлению и решению системы так называемых нормальных уравнений. Исходным этапом для этого является подбор вида функции, отображающей статистическую связь.

Тип функции в каждом конкретном случае можно подобрать путем прикидки на графике исходных данных подходящей, т. е. достаточно хорошо приближающей эти данные, линии. В нашем случае связь может быть изображена с помощью прямой линии  и записана в виде:

у=а0 + а1 х,

где ao и a1 — параметры уравнения, которые могут быть найдены методом наименьших квадратов.

Для нахождения искомых параметров нужно составить систему уравнений, которая в данном случае будет иметь вид:

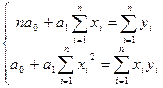
Полученная система может быть решена известным из школьного курса методом Гаусса. Искомые параметры системы из двух нормальных уравнений можно вычислить и непосредственно с помощью последовательного использования нижеприведенных формул:

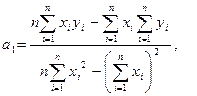
где yi — i-e значение результативного признака; xi — i-e значение факторного признака;  и — средние арифметические результативного и факторного признаков соответственно; n— число значений признака yi, или, что то же самое, число значений признака xi.


4.2 Интерпретация коэффициента регрессии

Уравнение регрессии не только определяет форму анализируемой связи, но и показывает, в какой степени изменение одного признака сопровождается изменением другого признака.

Коэффициент а1  при х, называемый коэффициентом регрессии, показывает, на какую величину в среднем изменяется результативный признак у при изменении факторного признака х на единицу.

4.3 Коэффициент детерминации

Когда уравнение регрессии уместно поставить уточняющий вопрос — какая часть вариации результативного признака может быть объяснена влиянием факторного признака.

Рассмотрим отношение:

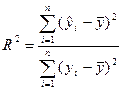
Оно показывает долю разброса, учитываемого регрессией, в общем разбросе результативного признака и носит название коэффициента детерминации. Этот показатель, равный отношению факторной вариации к полной вариации признака, позволяет судить о том, насколько «удачно» выбран вид функции (Отметим, что по смыслу коэффициент детерминации в регрессионном анализе соответствует квадрату корреляционного отношения для корреляционной таблицы). Проведя расчеты, основанные на одних и тех же исходных данных, для нескольких типов функций, мы можем из них выбрать такую, которая дает наибольшее значение R2 и, следовательно, в большей степени, чем другие функции, объясняет вариацию результативного признака. Действительно, при расчете R2 для одних и тех же данных, но разных функций знаменатель выражения для R2 остается неизменным, а числитель показывает ту часть вариации результативного признака, которая учитывается выбранной функцией. Чем больше R2, т. е. чем больше числитель, тем больше изменение факторного признака объясняет изменение результативного признака и тем, следовательно, лучше уравнение регрессии, лучше выбор функции.

Наконец, отметим, что введенный ранее, при изложении методов корреляционного анализа, коэффициент детерминации совпадает с определенным здесь показателем, если выравнивание производится по прямой линии. Но последний показатель (R2) имеет более широкий спектр применения и может использоваться в случае связи, отличной от линейной.

5. Нелинейная регрессия и нелинейная корреляция в общем случае

5.1 Построение уравнений нелинейной регрессии

Не всегда связь между признаками может быть достаточно хорошо представлена линейной функцией. Иногда для описания существующей связи более пригодными, а порой и единственно возможными являются более сложные нелинейные функции.

Одним из простейших видов нелинейной зависимости является парабола, которая в общем виде может быть представлена функцией:

у = а0+а1х+а2х2

Неизвестные параметры а0, а1, а2 находятся в результате решения следующей системы уравнений:

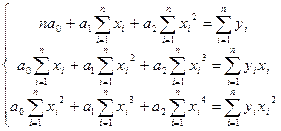
На практике для изучения связей используются полиномы более высоких порядков (3-го и 4-го порядков). Составление системы, ее решение, а также решение вопроса о полезности повышения порядка функции для этих случаев аналогичны описанным. При этом никаких принципиально новых моментов не возникает, но существенно увеличивается объем расчетов.

Кроме класса парабол для анализа нелинейных связей можно применять и другие виды функций. Для расчета неизвестных параметров этих функций рекомендуется использовать метод наименьших квадратов, как наиболее мощный и широко применяемый.

Однако метод наименьших квадратов не универсален, поскольку он может использоваться только при условии, что выбранные для выравнивания функции линейны по отношению к своим параметрам. Не все функции удовлетворяют этому условию, но большинство применяемых на практике с помощью специальных преобразований могут быть приведены к стандартной форме функции с линейными параметрами.

Рассмотрим некоторые простейшие способы приведения функций с нелинейными параметрами к виду, который позволяет применять к ним метод наименьших квадратов.

Функция

не является линейной относительно своих параметров.

Прологарифмировав обе части приведенного равенства, получаем:

и, переобозначив

получим функцию, линейную относительно своих новых параметров:

Кроме логарифмирования для приведения функций к нужному виду используют обратные величины.

Например, функция

с помощью следующих переобозначений:

y’=1/y, x’=1/x, 1/a0=a’0, a1/a0=a’1

может быть приведена к виду

Подобные преобразования расширяют возможности использования метода наименьших квадратов, увеличивая число функций, к которым этот метод применим.[4]

5.2 Измерение тесноты связи при криволинейной зависимости

Рассмотренные ранее линейные коэффициенты корреляции оценивают тесноту взаимосвязи при линейной связи между признаками. При наличии криволинейной связи указанные меры связи не всегда приемлемы.

Для измерения тесноты связи при криволинейной зависимости используется индекс корреляции, вычисляемый по формуле:

где уi—i-e значение результативного признака; ŷi—i-e выравненное значение этого признака; – среднее арифметическое значение результативного признака.

Числитель формулы индекса корреляции характеризует разброс выравненных значений результативного признака. Поскольку изменения выравненных, т. е. вычисленных по уравнению регрессии, значений признака происходят только в результате изменения факторного признака х, то числитель измеряет разброс результативного признака, обусловленный влиянием на него факторного признака. Знаменатель же измеряет разброс признака-результата, который определен влиянием на него всех факторов, в том числе и учтенного. Таким образом, индекс корреляции оценивает участие данного факторного признака в общем действии всего комплекса факторов, вызывающих колеблемость результативного признака, тем самым определяя тесноту зависимости признака у от признака х. При этом, если признак х не вызывает никаких изменений признака у, то числитель и, следовательно, индекс корреляции равны 0. Если же линия регрессии полностью совпадает с фактическими данными, т. е. признаки связаны функционально, то индекс корреляции равен 1. В случае линейной зависимости между х и у индекс корреляции численно равен линейному коэффициенту корреляции г. Квадрат индекса корреляции совпадает с введенным ранее  коэффициентом детерминации. Если же вопрос о форме связи не ставится, то роль коэффициента детерминации играет квадрат корреляционного отношения.

6. Аналитическое выравнивание ряда динамики

Наиболее эффективным способом выявления тенденции развития является аналитическое выравнивание.

Аналитическое выравнивание в каждом отдельном случае может быть осуществлено с помощью той или иной математической функции.

Наиболее простой функцией является прямая:

Параметры функции в данном случае определяются решением следующей системы уравнений:

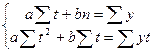
где п — число членов ряда;  у — текущее значение показателя.

Для упрощения расчетов принимают:

При этом текущие значения времени условно обозначают следующим образом. Если ряд нечетный, то срединное значение года принимают за нуль, до средины нумерация по порядку идет с минусом, далее с плюсом. Если ряд четный, то два срединных года принимаются вверх с минусом по нечету, вниз — с плюсом по нечету. Тогда нахождение параметров упрощается:

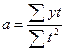  - (тренд, тенденция);

 -  (средний уровень ряда).


При аналитическом выравнивании по параболе второго порядка

система уравнений для определения ее параметров при  примет вид:

Для оценки аналитических уравнений рассчитывают показатели вариации, по которым судят о колеблемости аналитических рядов вокруг средней, корреляционное отношение и коэффициент детерминации, по которым судят о близости аналитических рядов к эмпирическому (фактическому):

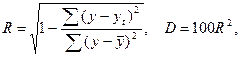
где R — корреляционное отношение; D — коэффициент детерминации.[5]

Заключение

Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания так или иначе определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики.

Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции.

Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.

По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно  положительными и отрицательными.

Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.

По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.

В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнения при интерпретации результатов и др.

Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак.

Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.

Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей.

Следует заметить, что традиционные методы корреляции и регрессии широко представлены в разного рода статистических пакетах программ для ЭВМ. Исследователю остается только правильно подготовить информацию, выбрать удовлетворяющий требованиям анализа пакет программ и быть готовым к интерпретации полученных результатов. Алгоритмов вычисления параметров связи существует множество, и в настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов интерпретации результатов является обязательным условием исследования.

Таковы основные принципы и условия, методика и техника применения корреляционного и регрессионного анализа. Их подробное рассмотрение обусловлено тем, что они являются высокоэффективными и потому очень широко применяемыми методами анализа взаимосвязей в объективном мире природы и общества.

Литература

1.          Гришин А.Ф. Статистика: Учеб. Пособие. – М.: Финансы и статистика, 2003.

2.          Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник.-М.:ИНФРА – М., 1996.

3.          Ефремова М.Р. «Общая теория статистики»; М.: «Инфра-М», 1996.

4.          Переяслова И.Г., Колбачев Е.Б., Переяслова О.Г. Статистика. Серия «Высшее образование». – Ростов н/Д: «Феникс», 2003.

5.          Экономическая статистика (под. ред. Ю.Н. Иванова) М.:ИНФРА-М, 1998.


[1] Гришин А.Ф. Статистика: Учеб. Пособие. – М.: Финансы и статистика, 2003, стр.134.


[2] Гришин А.Ф. Статистика: Учеб. Пособие. – М.: Финансы и статистика, 2003, стр.148.


[3] Переяслова И.Г., Колбачев Е.Б., Переяслова О.Г. Статистика. Серия «Высшее образование». – Ростов н/Д: «Феникс», 2003, стр.74.


[4] Переяслова И.Г., Колбачев Е.Б., Переяслова О.Г. Статистика. Серия «Высшее образование». – Ростов н/Д: «Феникс», 2003, стр.96.


[5] Гришин А.Ф. Статистика: Учеб. Пособие. – М.: Финансы и статистика, 2003, с.108.