Министерство образования Российской
Федерации
НОВОСИБИРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ
ЭКОНОМИКИ И
УПРАВЛЕНИЯ
Кафедра экономической информатики
Контрольная работа по информатике и
математике
Вариант №11
Выполнил:
Федоров Роман
Александрович
Проверил:
Новосибирск 2004
Задача 1.
Среди 150 школьников марки собирают только мальчики.
67 человек собирают марки России, 48 – марки Африки, 34 – марки Америки, 11 –
только марки России, 7 – только Африки и 2 – только Америки. Один Петя Галкин
собирает марки России, Америки и Африки. Какое максимальное число девочек может
быть среди 150 школьников?
Решение.
 Диаграмма
Эйлера-Вена:
Диаграмма
Эйлера-Вена:
Обозначим через
МВ
– минимальное количество всех мальчиков;
МР – количество мальчиков, собирающих марки только России;
МА
– количество мальчиков, собирающих марки только Америки;
МФ
– количество мальчиков, собирающих марки только Африки;
МРА
– количество мальчиков, собирающих марки только России и Америки;
МРФ
– количество мальчиков, собирающих марки только России и Африки;
МАФ – количество мальчиков, собирающих
марки только Америки и Африки;
МРАФ
– количество мальчиков, собирающих марки России, Америки и Африки.
По условию
задачи, так как 67 человек собирают
марки России, получаем:
МР +
МРА + МРФ + МРАФ = 67 (условие 1).
Так как 48 человек собирают марки Африки, получаем:
МФ +
МРФ+ МАФ + МРАФ = 48 (условие 2).
Так как 34 человека собирают марки Америки, то
МА + МРА+ МАФ +
МРАФ = 34 (условие 3).
Так как 11 человек собирают только
марки России, то
МР=
11 (условие 4).
Так как 7 человек собирают только марки Африки, то
МФ =7 (условие 5).
Так как 2 человека собирают марки только Америки, то
МА
= 2 (условие 6).
Так как один Петя Галкин собирает марки России,
Америки и Африки, то
МРАФ
= 1 (условие 7).
Требуется найти
150 – МВ.
Отметим
известные значения на диаграмме Эйлера-Вена:
Пусть МРА
= х. Тогда из условия 1 получаем: 11+х+МРФ+1 = 67. Следовательно, МРФ
= 55 - х.
Из условия
2: 2+(55-х)+МАФ+1
= 48, МАФ =
х-10 .
По условию 3: 7+х+(х-10)+1 = 34, х=18.
Получаем: МРА=18, МРФ=37, МАФ
=8.
Тогда МВ=МР + МА +
МФ + МРА+МРФ +МАФ + МРАФ=11+7+2+18+37+8+1=84
Таким образом, 84 мальчика собирают марки. Число
девочек будет максимальным, если нет
мальчиков, которые не собирают марки.
Получаем:
150 – МВ = 150-84 =66.
Ответ:
Среди 150 школьников максимальное число девочек
может быть 66.
Задача 11.
Если
понятые не приглашены, то процессуальный порядок следственного действия не
соблюден. Понятые не приглашены. Следовательно, процессуальный порядок
следственного действия не соблюден.
Решение.
Обозначим
высказывания:
А – «понятые не приглашены»;
В – «процессуальный порядок следственного действия не
соблюден»
Данное
рассуждение можно представить в виде формулы:
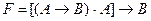 .
.
Проверим
формулу на тождественную истинность.
Составляем таблицу истинности:
|
А
|
В
|
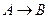
|
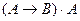
|
F
|
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
Так как формула F
является тождественно истинной, данное рассуждение верно.
Задача 21.
По
заданной функции проводимости построить СКНФ и СДНФ. Упростить полученные
формулы:
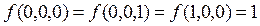 .
.
Решение.
Исходя из условия, построим таблицу истинности
заданной функции проводимости:
|
х
|
y
|
z
|
f(x,y,z)
|
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
0
|
По
наборам, на которых функция равна 1, строим СДНФ:
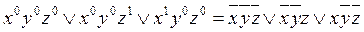
По
наборам, на которых функция равна 0, строим СКНФ:
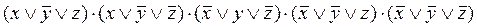 .
.
Упростим
СДНФ:
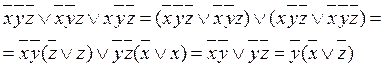
Для проверки равносильности формул составим таблицу истинности формулы 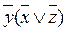 :
:
|
х
|
y
|
z
|
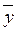
|
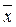
|
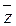
|
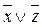
|
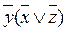
|
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
Так как таблицы истинности для f(x,y,z) и
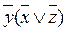 совпадают, формулы эквивалентны.
совпадают, формулы эквивалентны.
Литература.
1.
Информатика. Учебник/ Под ред. проф. Н.В.Макаровой.
– М.: Финансы статистика, 1997.
2.
Информатика и математика и для юристов: Учеб.
пособие для вузов/ Под ред. проф.
Х.А.Андриашина, проф. С.Я. Казанцева. – М.: ЮНИТИ-ДАНА, Закон и право, 2001.
3.
Богатов Д.Ф., Богатов Ф.Г. Основы
информатики и математики для юристов: Учеб. пособие. В 2-х томах. М.: ПРИОР,
2000.