Министерство образования Российской
Федерации
НОВОСИБИРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ
ЭКОНОМИКИ И
УПРАВЛЕНИЯ
Кафедра экономической информатики
Контрольная работа по информатике и
математике
Вариант №8
Выполнил:
Покорский Игорь Олегович
Проверил:
Новосибирск 2004
Задача 8.
На кафедре иностранных языков работают 37
преподавателей, из них французский преподают 23 преподавателя, английский – 16.
Число преподавателей, ведущих занятия только по
английскому языку равно числу преподавателей, ведущих занятия только по
немецкому. Число преподавателей, ведущих занятия только по английскому и немецкому языкам равно числу
преподавателей, ведущих занятия только по немецкому и французскому языкам.
Преподавателей, ведущих только французский и английский, на кафедре нет. Все
три языка ведут 3 преподавателя. Сколько преподавателей преподают один
английский язык?
Решение.
Обозначим через
МА – количество преподавателей, преподающих только английский
язык;
МН – количество преподавателей, преподающих только немецкий язык;
МФ – количество преподавателей,
преподающих только французский язык;
МАН – количество преподавателей,
преподающих только английский и немецкий языки;
МАФ – количество преподавателей,
преподающих только английский и французский языки;
МНФ
– количество преподавателей, преподающих только немецкий и французский языки;
МАНФ
– количество преподавателей, преподающих три языка.
По условию задачи,
так как французский преподают 23 преподавателя, получаем:
МФ
+ МАФ + МНФ + МАНФ = 23 (условие 1).
Так как английский
преподают 16 преподавателя, получаем:
МА
+ МАН + МАФ + МАНФ = 16 (условие 2).
Так как число преподавателей, ведущих занятия только
по английскому языку равно числу
преподавателей, ведущих занятия только по немецкому, то
МА
= МН (условие 3).
Так как число
преподавателей, ведущих занятия только по
английскому и немецкому языкам равно числу преподавателей, ведущих
занятия только по немецкому и французскому языкам, то
МАН
= МНФ (условие 4).
Так как преподавателей, ведущих только французский и
английский, на кафедре нет, то
МАФ = 0
(условие 5).
Так как все три языка ведут 3 преподавателя, то
МАНФ
= 3 (условие 6).
Так как на кафедре иностранных языков работают 37
преподавателей, то
МА + МН + МФ + МАН
+ МАФ + МНФ + МАНФ=37 (условие 7).
Требуется найти МА.
Диаграмма Эйлера-Вена:
Обозначим МА
= х. Тогда из условия 3 получаем: МН = МА = х .
Из условий
2, 5 и 6: х+МАН +0+3 = 16, МАН = 13 – х. .
Следовательно, по условию 4: МНФ = МАН
= 13 – х.
Из условий 1,5 и 6 получаем: МФ + 0
+ (13-х) + 3 = 23, МФ = 7+х.
Подставляя
найденные значения в условие 7, получаем:
х+х+(7+х)+(13-х)+0+(13-х)+3=37,
х=1.
Ответ: 1 преподаватель преподает один
английский язык.
Задача 18.
Если
сегодня вечером будет мороз, то я пойду на каток. Если завтра будет оттепель,
то я пойду в музей. Сегодня вечером будет мороз или завтра будет оттепель.
Следовательно, я пойду на каток и в музей.
Решение.
Обозначим
высказывания:
А – «сегодня вечером будет мороз»;
В – «завтра будет оттепель »;
С – «я пойду на каток»;
D – «я пойду в
музей».
Данное
рассуждение можно представить в виде формулы:
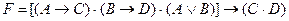 .
.
Проверим
формулу на тождественную истинность.
Введем
обозначение: 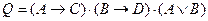
Составляем таблицу истинности:
|
А
|
B
|
C
|
D
|
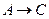
|
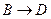
|
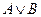
|
Q
|
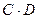
|
F
|
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
Так как формула F
не является тождественно истинной, данное рассуждение неверно.
Задача 28.
По
заданной функции проводимости построить СКНФ и СДНФ. Упростить полученные
формулы:
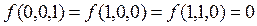 .
.
Решение.
Исходя из условия, построим таблицу истинности
заданной функции проводимости:
|
х
|
y
|
z
|
f(x,y,z)
|
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
По
наборам, на которых функция равна 1, строим СДНФ:
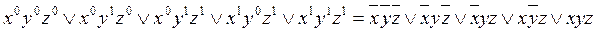
По
наборам, на которых функция равна 0, строим СКНФ:
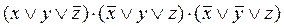 .
.
Упростим
СДНФ:
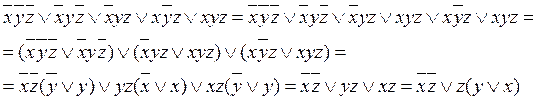
Для проверки равносильности формул составим таблицу истинности формулы  :
:
|
х
|
y
|
z
|
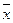
|
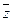
|
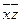
|
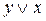
|
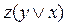
|

|
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
Так как таблицы истинности для f(x,y,z) и
 совпадают, формулы эквивалентны.
совпадают, формулы эквивалентны.
Литература.
1.
Информатика. Учебник/ Под ред. проф. Н.В.Макаровой.
– М.: Финансы статистика, 1997.
2.
Информатика и математика и для юристов: Учеб.
пособие для вузов/ Под ред. проф.
Х.А.Андриашина, проф. С.Я. Казанцева. – М.: ЮНИТИ-ДАНА, Закон и право, 2001.
3.
Богатов Д.Ф., Богатов Ф.Г. Основы
информатики и математики для юристов: Учеб. пособие. В 2-х томах. М.: ПРИОР,
2000.