ОГЛАВЛЕНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ ЭКОНОМЕТРИКИ.. 3
2. ПОСТРОЕНИЕ ПАРНОЙ РЕГРЕССИОННОЙ МОДЕЛИ.. 4
3. ПОСТРОЕНИЕ МНОЖЕСТВЕННОЙ РЕГРЕССИОННОЙ МОДЕЛИ. 6
4. ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ. РЯД ФУРЬЕ. 8
5. МАРКОВСКИЕ ЦЕПИ.. 11
ЛИТЕРАТУРА.. 13
1. ОСНОВНЫЕ
ПОНЯТИЯ ЭКОНОМЕТРИКИ
Задание.
1. Определите, на
какой диаграмме показаны временные данные, а на какой пространственные.
2. Дайте определение регрессии.
3. Определите виды регрессий:
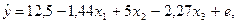
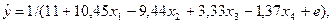
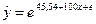 .
.
Покажите, где здесь результирующая и
объясняющие переменные. Что обозначает е в уравнениях регрессии?
Решение.
1. На рис. 1 показаны
временные данные, на рис.2 – пространственные.
2. Регрессия - односторонняя
вероятностная зависимость между случайными величинами.
3. 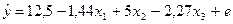 - это
множественная линейная регрессия, у - результирующая, х1,
х2, х3 - объясняющие переменные, е - ошибка
регрессии.
- это
множественная линейная регрессия, у - результирующая, х1,
х2, х3 - объясняющие переменные, е - ошибка
регрессии.
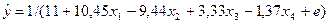 - это множественная гиперболическая регрессия, у
- результирующая, х1, х2, х3, х4
- объясняющие переменные, е - ошибка регрессии.
- это множественная гиперболическая регрессия, у
- результирующая, х1, х2, х3, х4
- объясняющие переменные, е - ошибка регрессии.
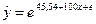 - это простая экспоненциальная регрессия, у
- результирующая, х – объясняющая переменная, е - ошибка
регрессии.
- это простая экспоненциальная регрессия, у
- результирующая, х – объясняющая переменная, е - ошибка
регрессии.
2.
ПОСТРОЕНИЕ ПАРНОЙ РЕГРЕССИОННОЙ МОДЕЛИ
Задание.
1. Дайте определение парной
регрессии.
2. По Российской Федерации за 2001
год известны значения двух признаков (см. табл. 1).
Таблица 1
|
Месяц
|
Расходы на
покупку продо- вольственных товаров в общих расходах, %, (у)
|
Средний
денежный доход на душу населения, руб., (х)
|
|
Январь
|
69
|
1964,7
|
|
Февраль
|
65,6
|
2292,0
|
|
Март
|
60,7
|
2545,8
|
|
Апрель
|
...
|
...
|
|
Май
|
...
|
...
|
|
Июнь
|
...
|
...
|
|
Июль
|
...
|
...
|
|
Август
|
...
|
...
|
|
Сентябрь
|
...
|
...
|
|
Октябрь
|
53,3
|
3042,8
|
|
Ноябрь
|
50,9
|
3107,2
|
|
Декабрь
|
47.5
|
4024,7
|
Для оценки зависимости у от х
построена парная линейная регрессионная модель с помощью метода наименьших
квадратов:
у=а+bх+е, где а = 194/4 = 48,5, b = -1/194=0,005.
Парный коэффициент корреляции rxy = -1/194 х 78 = -78/194 =
-39/97=-0,402
Средняя ошибка аппроксимации 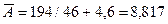 .
.
Известно, что 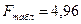 , а
, а 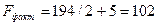 .
.
Определите коэффициент детерминации. Оцените линейную модель
через среднюю ошибку аппроксимации и F-критерий Фишера.
Решение.
1. Парная регрессия -
уравнение связи между двумя переменными у и х.
2. Так как а = 194/4 = 48,5, b = -1/194, получим уравнение
регрессии
у=48,5-0,005х+е,
Значит, с увеличением среднего денежного дохода на 1
руб. доля расходов на покупку продовольственных товаров снижается в среднем на
0,005 %.
Линейный коэффициент парной корреляции 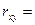 - 0,402 (связь
умеренная, обратная).
- 0,402 (связь
умеренная, обратная).
Найдем коэффициент детерминации, 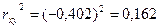 . Вариация результата на 16,2 % объясняется вариацией фактора
х.
. Вариация результата на 16,2 % объясняется вариацией фактора
х.
Средняя ошибка аппроксимации А = 8,817, что
говорит о допустимой ошибке аппроксимации. В среднем расчетные значения
отклоняются от фактических на 8,817 %.
Проверяем F-критерий Фишера. Для этого сравним 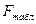 и
и 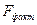 .
.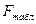 <
< 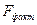 (4,96 < 102),
значит Н0 - гипотеза о случайной природе оцениваемых характеристик
отклоняется и признается их статистическая значимость и надежность с
вероятностью 0,95.
(4,96 < 102),
значит Н0 - гипотеза о случайной природе оцениваемых характеристик
отклоняется и признается их статистическая значимость и надежность с
вероятностью 0,95.
Вывод.
Линейная парная модель не очень хорошо описывает изучаемую закономерность.
3.
ПОСТРОЕНИЕ МНОЖЕСТВЕННОЙ РЕГРЕССИОННОЙ МОДЕЛИ.
Задание.
1. В табл. 2 приведены данные,
формирующие цену на строящиеся квартиры в двух различных районах.
Таблица 2
|
Район,
а/б
|
Жилая
площадь,
м2
|
Площадь
кухни, м2
|
Этаж, сред-
ние/крайние
|
Дом, кир-
пич./панел.
|
Срок сдачи,
через сколько
мес.
|
Стоимость
квартиры,
тыс.дол.
|
|
1
|
17,5
|
8
|
1
|
1
|
6
|
17,7
|
|
1
|
20
|
8,2
|
1
|
2
|
1
|
31,2
|
|
2
|
23,5
|
11,5
|
2
|
2
|
9
|
13,6
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
1
|
77
|
17
|
2
|
1
|
1
|
56,6
|
|
2
|
150,5
|
30
|
2
|
2
|
2
|
139,2
|
|
2
|
167
|
31
|
2
|
1
|
5
|
141,5
|
Имеется шесть факторов,
которые могут оказывать влияние на цену строящегося жилья:
1) район, где расположена строящаяся квартира (а или
б);
2) жилая площадь квартиры;
3) площадь кухни;
4) этаж (средний или крайний);
5) тип дома (панельный или кирпичный);
6) срок сдачи квартиры (через сколько месяцев).
Определите минимальный объем выборки Nmin.
Для оценки зависимости у от х построена
линейная множественная регрессионная модель с помощью метода наименьших
квадратов
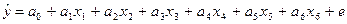 ,
,
где 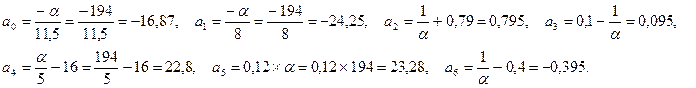
Какие фиктивные переменные были использованы в модели?
Дайте экономическую интерпретацию полученной модели.
Решение.
Найдем
минимальный объем выборки Nmin
. Число факторов, включаемых в модель, т = 6, а число свободных членов в
уравнении п = 1. Тогда
Nmin = 5(6+1)=35.
Получаем уравнение регрессии
у= -16,87 – 24,25х1 + 0,795х2 + 0,095х3
+ 22,8х4 + 23,28х5 - 0,395х6
+ е.
Фиктивными переменными являются х1, х4,
х5, так как они соответствуют качественным признакам.
Экономическая интерпретация полученной модели:
квартиры в районе а стоят на 24,25 % дешевле, чем в районе б. При
увеличении жилой площади на 1 % стоимость квартиры возрастает на 0,795%. При
увеличении площади кухни на 1 % стоимость квартиры увеличивается на 0,095%.
Квартиры на средних этажах стоят на 22,8 % дороже, чем на крайних. Квартиры в
кирпичных домах стоят на 23,28 % дороже, чем в панельных. При увеличении срока
сдачи дома на 1% стоимость квартиры уменьшается на 0,395 %.
4.
ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ. РЯД ФУРЬЕ.
Задание.
Постройте
модель сезонных колебаний дохода торгового предприятия, используя первую
гармонику ряда Фурье по данным, приведенным в табл. 3, изобразите графически.
Таблица 3
|
Месяц
|
Доход, тыс.
руб.
|
|
Январь
|
58,33+112´(1/a)
|
|
Февраль
|
52+112´(1/a)
|
|
Март
|
43,67+112´(1/a)
|
|
Апрель
|
41,02+112´(1/a)
|
|
Май
|
42,77+112´(1/a)
|
|
Июнь
|
50,01+112´(1/a)
|
|
Июль
|
56,6+112´(1/a)
|
|
Август
|
64,74+112´(1/a)
|
|
Сентябрь
|
71,04+112´(1/a)
|
|
Октябрь
|
73,54+112´(1/a)
|
|
Ноябрь
|
72,16+112´(1/a)
|
|
Декабрь
|
66,3+112´(1/a)
|
Воспользуйтесь вспомогательной табл. 4.
Таблица 4
|
t
|
cos t
|
sin t
|
|
0
|
1,00
|
0,00
|
|
0,523599
|
0,87
|
0,50
|
|
1,047198
|
0,50
|
0,87
|
|
1,570796
|
0,00
|
1,00
|
|
2,094395
|
-0,50
|
,0,87
|
|
2,617994
|
-0,87
|
0,50
|
|
3,141593
|
-1,00
|
0,00
|
|
3,665191
|
-0,87
|
-0,50
|
|
4,18879
|
-0,50
|
-0,87
|
|
4,712389
|
0,00
|
-1,00
|
|
5,235988
|
0,50
|
-0,87
|
|
5,759587
|
0,87
|
-0,50
|
Решение.
Для a
= 194 исходная таблица будет выглядеть
следующим образом:
Таблица 5
|
Месяц
|
Периоды,
|
Доход,тыс.руб.
|
|
Январь
|
0
|
58,91
|
|
Февраль
|
0,5236
|
52,58
|
|
Март
|
1,0471
|
44,25
|
|
Апрель
|
1,5707
|
41,6
|
|
Май
|
2,0943
|
43,35
|
|
Июнь
|
2,618
|
50,59
|
|
Июль
|
3,1416
|
57,18
|
|
Август
|
3,6652
|
65,32
|
|
Сентябрь
|
4,1888
|
71,62
|
|
Октябрь
|
4,7124
|
74,12
|
|
Ноябрь
|
5,236
|
72,74
|
|
Декабрь
|
5,7596
|
66,88
|
Если мы рассматриваем год как цикл,
то п =12. Параметры уравнения
могут быть найдены по формулам:
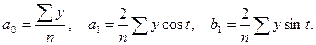
Получили а0 =
58,26. Найдем промежуточные значения 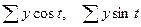 (табл. 6).
(табл. 6).
Таблица 6
|
Месяц
|
Периоды, t
|
Доход,тыс.руб.
|
у´соs t
|
у´sin t
|
|
Январь
|
0
|
58,91
|
58,91
|
0
|
|
Февраль
|
0,5236
|
52,58
|
45,7446
|
26,29
|
|
Март
|
1,0471
|
44,25
|
22,125
|
38,4975
|
|
Апрель
|
1,5707
|
41,6
|
0
|
41,6
|
|
Май
|
2,0943
|
43,35
|
-21,675
|
37,7145
|
|
Июнь
|
2,618
|
50,59
|
-44,013
|
25,295
|
|
Июль
|
3,1416
|
57,18
|
-57,18
|
0
|
|
Август
|
3,6652
|
65,32
|
-56,828
|
-32,66
|
|
Сентябрь
|
4,1888
|
71,62
|
-35,81
|
-62,309
|
|
Октябрь
|
4,7124
|
74,12
|
0
|
-74,12
|
|
Ноябрь
|
5,236
|
72,74
|
36,37
|
-63,284
|
|
Декабрь
|
5,7596
|
66,88
|
58,1856
|
-33,44
|
Получаем: 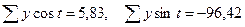 .
.
Найдем коэффициенты: 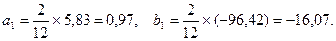
Получили yt = 58,26 + 0,97´соs t - 16,07´sin t. Подставим фактические значения t в полученную первую гармонику ряда
Фурье.
Таблица 7
|
Месяц
|
Периоды, t
|
yt
|
|
Январь
|
0
|
59,2331
|
|
Февраль
|
0,5236
|
51,0721
|
|
Март
|
1,0471
|
44,7670
|
|
Апрель
|
1,5707
|
42,1923
|
|
Май
|
2,0943
|
43,7956
|
|
Июнь
|
2,618
|
49,3819
|
|
Июль
|
3,1416
|
57,2903
|
|
Август
|
3,6652
|
65,4512
|
|
Сентябрь
|
4,1888
|
71,7563
|
|
Октябрь
|
4,7124
|
74,3310
|
|
Ноябрь
|
5,236
|
72,7277
|
|
Декабрь
|
5,7596
|
67,1415
|
Строим график исходных данных и
первой гармоники ряда Фурье 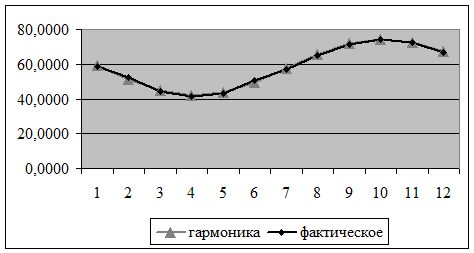
Рис. 3. Первая гармоника ряда Фурье
5. МАРКОВСКИЕ ЦЕПИ
Задание.
В торгово-розничную сеть поступило 3
вида взаимозаменяемой продукции разных производителей: А1, А2, АЗ. Предположим,
что покупатели приобретают продукцию только одного из них. Пусть в среднем они
стремятся поменять её не более одного раза в год, и вероятности таких изменений
постоянны.
Результаты маркетинговых исследований
покупательского спроса на продукцию дали следующее процентное соотношение:
X1 % покупателей продукции А1 переходит на продукцию
А2,
Х2 % покупателей продукции А2 - на продукцию АЗ,
ХЗ % покупателей продукции АЗ - на продукцию А1,
где 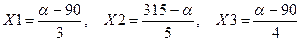 .
.
Требуется:
1. Построить граф состояний.
2. Составить матрицу переходных
вероятностей для средних годовых изменений.
3. Предположить, что общее число
покупателей постоянно, и определить, какая доля из их числа будет покупать
продукцию А1, А2 и АЗ через 2 года.
4. Определить какая продукция будет
пользоваться наибольшим спросом.
Решение.
 Для
a =194 получаем: X1 = (194 - 90):3 = 34,7; Х2
= (315 – 194):5 = 24,2; ХЗ = (194 - 90):4 = 26.
Для
a =194 получаем: X1 = (194 - 90):3 = 34,7; Х2
= (315 – 194):5 = 24,2; ХЗ = (194 - 90):4 = 26.
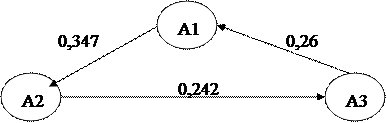
Построим граф состояний:
Составим матрицу переходных
вероятностей:
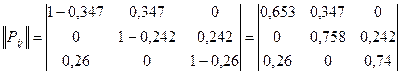
Зададим вектор начальных
вероятностей:
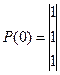 .
.
Определим вероятности состояния Рi(к) после первого шага (после первого
года):
Р1(1)
= Р1(0)Р11
+Р2(0)×Р21 +Р3(0)×Р31
=1×0,653+1×0+1×0,26 = 0,913;
Р2(1)= Р1(0)Р12
+Р2(0)×Р22 +Р3(0)×Р32 =1×0,347+1×0,758 +1×0
=1,105;
Рз(1) = Р1(0)Р13
+Р2(0)×Р23 +Р3(0)×Р33
=1×0+1×0,242+1×0,74 = 0,982.
Определим вероятности состояний после
второго шага (после второго года):
Р1(2)=Р1(1)Р11 +Р2(1)×Р21
+Р3(1)×Р31 = 0,913×0,653+1,105×0+0,982×0,26
= 0,852;
Р2(2)=Р1(1)Р12
+Р2(1)×Р22 +Р3(1)×Р32
=0,913×0,347+1,105×0,758+0,982×0
= 1,154;
Р3(2) = Р1(1)Р13
+Р2(1)×Р23 +Р3(1)×Р33
= 0,913×0+1,105×0,242+0,982×0,74
= 0,99.
Вывод. Через 2 года 85% покупателей будут приобретать продукцию
А1, 99% покупателей - АЗ, число
покупателей продукции А2 увеличится почти в 1,2 раза.
Продукция А2 будет пользоваться
наибольшим спросом.
ЛИТЕРАТУРА
1. Айвазян С. А., Мхитарян В. С.
Прикладная статистика и основы эконометрики. -М.: ЮНИТИ, 1998.
2. Бережная Е. В., Бережной В. И. Математические
методы модели-рования экономических систем. - М.: Финансы и статистика, 2001. -
368 с.
3. Елисеева И. И. и др. Практикум по эконометрике. -
М.: Финансы и статистика, 2001. - 192 с.
4. Магнус Я. Р., Катышев П. К., Пересецкий А. А.
Эконометрика. Начальный курс. - М.: Дело, 2000. - 400 с.
5. Маленво Э. Статистические методы эконометрики. -
М.: Статистика, 1975. - Т. 1; 1976. - Т. 2.