Оглавление
Введение. 2
1. Теоретическая
часть. 4
3.1 Показатели
уровня производительности труда. 4
3.2 Характеристика
динамики производительности труда. 9
Помимо уровней производительности труда,
статистика также изучает и динамику производительности труда, что решается с
помощью индексов. 9
По отдельным
видам продукции (работ, услуг) осуществляется расчет отдельных индексов
как по прямым, так и по обратным показателям производительности труда. 9
Так для прямых показателей индивидуальный индекс
производительности труда можно записать так: 9
3.3 Статистические
методы измерения влияния факторов роста производительности труда. 13
3.4 Построение
индексных моделей для изучения влияния динамики труда и отработанного времени
на изменение объема выпуска продукции. 14
2. Расчетная
часть. 15
Задание 1. 15
Задание 2. 21
Задание 3. 28
Задание 4. 30
3. Аналитическая
часть. 35
3.1 Постановка
задачи: 35
3.2 Методика
решения задачи. 36
3.3 Технология
выполнения компьютерных расчетов. 37
3.4 Анализ
результатов статистических компьютерных расчетов. 39
Заключение. 40
Список литературы.. 43
Приложение. 44
Введение
Производительность труда является одним
из важнейших качественных показателей работы предприятия, выражением
эффективности затрат труда. От уровня производительности труда зависят темпы
развития промышленного производства, увеличение заработной платы и доходов,
размеры снижения себестоимости продукции. Повышение производительности труда
путем механизации и автоматизации труда, внедрения новой техники и технологии
практически не имеет границ. Поэтому целью анализа производительности труда
является выявление возможностей дальнейшего увеличения выпуска продукции за
счет роста производительности труда, более рационального использования
работающих и их рабочего времени.
Основные задачи статистики
производительности труда связаны с расчетом уровня производительности труда,
его динамики, с выявлением влияния различных факторов на изменение
производительности труда, а также с выявлением влияния производительности труда
на объем выпускаемой продукции.
В теоретической части курсовой работы рассмотрены следующие
аспекты:
1. Показатели
уровня производительности труда.
2. Характеристика
динамики производительности труда.
3. Статистические
методы измерения влияния факторов роста производительности труда.
4. Построение индексных
моделей для изучения влияния динамики труда и отработанного времени на изменение
объема выпуска продукции.
Расчетная часть курсовой работы включает решение четырех заданий по теме из
варианта расчетного задания:
1. Исследование структуры совокупности.
2. Выявление наличия корреляционной
связи между признаками, установление направления связи и измерение ее тесноты.
3. Применение выборочного метода.
4. Использование индексного метода.
Аналитическая часть работы представляет
собой анализ временного ряда (определение абсолютного прироста; темпа роста;
темпа прироста; абсолютного значения 1% прироста; средних за период уровня
ряда, абсолютного прироста, темпа роста и прироста) с использованием программы
обработки электронных таблиц Excel пакета Microsoft Office 2003 в среде Windows XP.
В работе использовались учебники
базового курса, дополнительная литература, а также Интернет-ресурсы.
1. Теоретическая
часть
3.1 Показатели
уровня производительности труда
Производительность
труда – это
результативность конкретного труда, эффективность целесообразной
производительной его деятельности по созданию продукта в течение определенного
периода времени.
Характеризуя
эффективность затрат труда в материальном производстве, производительность
труда определяется количеством продукции, производимой в единицу рабочего
времени, или затратами труда на единицу продукции. Чем больше продукции
создается в единицу времени, тем выше производительность труда.
Различают
производительность живого труда и производительность общественного
(совокупного) труда.
Производительность живого
труда определяется затратами времени в данном производстве, на данном
предприятии, а производительность общественного труда – затратами живого и
прошлого труда, произведенными на предшествующих стадиях общественного
производства и овеществленные в сырье, материалах, топливе, энергии, орудиях
труда, потребляемых на данном предприятии в процессе производства продукции. По
мере научно-технического прогресса, совершенствования производства доля затрат
общественного труда увеличивается, поскольку растет оснащенность работника все
новыми средствами труда (от простейших машин до электронных комплексов). Однако
основная тенденция состоит в том, что абсолютная величина затрат как живого,
так и общественного труда на единицу продукции сокращается. Именно в этом
сущность повышения производительности общественного труда.
Уровень
производительности труда измеряется двумя показателями: прямым показателем –
выработкой и обратным – трудоемкостью.
Выработка продукции в
единицу затраченного рабочего времени – наиболее распространенный и универсальный показатель
производительности труда. В связи с тем, что затраты рабочего времени могут
быть выражены количеством отработанных человеко-часов, человеко-дней, средним
списочным числом рабочих или всех работников предприятия, различают показатели
средней часовой, средней дневной выработки и показатели средней выработки на
одного списочного рабочего или работника всего персонала, непосредственно
связанного с производством данной продукции.
Средняя часовая
выработка
определяется путем деления количества выработанной продукции за какой-либо
период на число фактически отработанных за этот период человеко-часов.
Средняя дневная
выработка
определяется делением количества выработанной продукции за какой-либо период на
число отработанных за этот период человеко-дней. Отработанные человеко-дни
включают в себя время чистой работы и время внутрисменных перерывов в работе и
простоев. Поэтому величина средней дневной выработки зависит от уровня средней
часовой выработки и фактической продолжительности рабочего дня.
Средняя месячная
(квартальная, годовая) выработка вычисляется путем деления выработанной за изучаемый период
продукции на среднюю списочную численность рабочих (или работников).
Пример вычисления средней
годовой выработки приведен в табл. 1.1:
Таблица
1.1
Нахождение среднегодовой выработки малых
предприятий Тульской области*
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
Среднесписочная численность работников, чел.
|
53932
|
54582
|
55247
|
59314
|
57793
|
|
Объем продукции (работ, услуг), млн. руб.
|
4661,3
|
5890,3
|
6438,8
|
8234,2
|
11554,0
|
|
Среднегодовая выработка, тыс. руб.
|
86,429
|
107,917
|
116,546
|
138,824
|
119,920
|
*Построено
по данным табл. «Основные экономические показатели деятельности малых
предприятий», источник: Тульский статистический ежегодник, 2006. – Тула:
Туластат. – 2007. – с.131.
Из
таблицы 1.1 видно, что среднегодовая выработка, т.е. производительность труда
малых предприятий Тульской области увеличилась за период с 2000г. по 2004г.
более чем в 2 раза. Отобразим динамику производительности труда малых
предприятий Тульской области на диаграмме (рис.1.1).
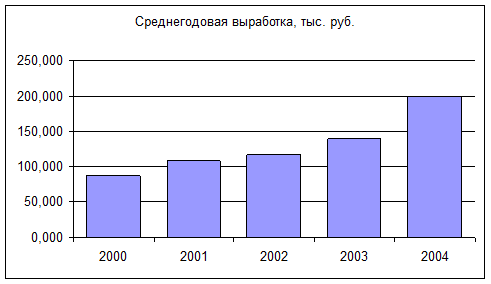
Рисунок 1.1 Диаграмма
динамики производительности труда на малых предприятиях Тульской области
Все
вышеперечисленные показатели средней
выработки взаимосвязаны:
Средняя дневная выработка = Средняя часовая
выработка × Средняя продолжительность рабочего дня;
Средняя месячная (квартальная, годовая)
выработка на одного рабочего = Средняя дневная выработка × Средняя
продолжительность рабочего месяца (квартала, года);
Средняя месячная (квартальная, годовая)
выработка одного работника = Средняя месячная (квартальная, годовая) выработка
одного рабочего × Доля рабочих в общей численности работающих.
Аналогичная
взаимосвязь существует между показателями динамики рассматриваемых уровней.
Выработка
(W) продукции в единицу времени определяется соотношением:
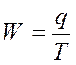 ,
,
где q - объем
произведенной продукции,
Т - затраты
рабочего времени.
Трудоемкость
(t) изготовления единицы продукции (обратный показатель производительности
труда) характеризуется затратами рабочего времени на единицу произведенной
продукции:
 .
.
По
определению, между рассмотренными величинами существуют зависимости, которые
могут быть использованы в экономических расчетах:
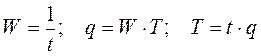 .
.
В
зависимости от способа исчисления объема продукции (числителя показателя
выработки) статистика использует в наиболее общем плане три метода измерения
производительности труда: натуральный, трудовой и стоимостной (ценностный). Каждый
из них имеет определенное экономическое значение и границы применения.
·
натуральный
метод
Используется в условиях
выпуска однородной продукции. При использовании этого метода объем
произведенной продукции выражается в натуральных единицах измерения (тоннах,
метрах, литрах и т.д.). Натуральные показатели возможно и целесообразно
применять для характеристики производительности труда в бригадах, на участках и
на индивидуальном рабочем месте.
·
трудовой
метод
При этом общий объем
результатов производства выражают в некоторых фиксированных единицах
трудоемкости. В этом случае уровни производительности труда с определенной
степенью условности характеризуются величиной отдачи результата фактических
затрат труда. На практике возникает вопрос о выборе измерителя – фиксированной
величины трудоемкости единицы продукции каждого вида. Чаще всего пользуются
нормативной величиной трудоемкости единицы продукции.
·
стоимостной
метод
Этот метод целесообразно
использовать в условиях выпуска разнородной продукции. При использовании
стоимостного метода объем произведенного результата производства оценивается в
денежном выражении через цену или, что является более предпочтительным через
добавленную стоимость. Дело в том, что при расчете объемов продукции в
отпускных ценах в сумму данных всех подразделений войдет, по существу, величина
валового оборота, а не валовой или товарной продукции предприятия в целом. При
использовании же показателей добавленной стоимости проблема повторного счета
оказывается равной стоимости, добавленной обработкой по фирме в целом.
Сопоставив объем
продукции с соответствующими затратами живого труда, получим стоимостной
показатель уровня производительности труда, который можно выразить
следующей формулой:
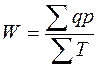 ,
,
где ∑qp – объем продукции в денежном выражении,
∑Т – затраты труда на изготовление указанного объема продукции.
Производительность
общественного труда (по экономике в целом) рассчитывается как отношение
произведенного валового национального дохода (ВНД) к среднегодовой численности
занятых в сфере материального производства. С переходом к международной
методологии уровень производительности общественного труда определяется
отношением ВВП в рыночных ценах к среднегодовой численности экономически
активного населения.
3.2 Характеристика
динамики производительности труда
Помимо уровней производительности труда, статистика также
изучает и динамику производительности труда, что решается с помощью индексов.
По отдельным видам
продукции (работ, услуг) осуществляется расчет отдельных индексов как по
прямым, так и по обратным показателям производительности труда.
Так для прямых показателей индивидуальный индекс
производительности труда можно записать так:
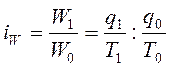
(символы те же, что и в предыдущих
формулах).
Для
обратных показателей (трудоемкости) индивидуальный индекс производительности
труда:
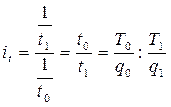 .
.
В
зависимости от того, в каких единицах выражена продукция, а следовательно и
средняя выработка, сопоставляемая за два периода, общие индексы принято
исчислять натуральным, трудовым и стоимостным методами.
Натуральный
индекс производительности труда:
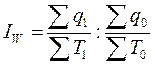 ,
,
где q1, q0 – объемы продукции в натуральном
выражении в отчетном и базисном периодах соответственно,
Т1, Т0
– затраты труда на производство данной продукции в отчетном и базисном периодах
соответственно.
Трудовой
индекс производительности труда:
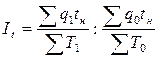 ,
,
где tн – фиксированные уровни трудоемкости
– нормативная трудоемкость, т.е. затраты труда по норме на производство единицы
продукции.
Т.к.
единицы измерения трудоемкости для сравниваемых периодов фиксированы, то
динамика производительности труда оценивается достаточно точно.
В
случаях, когда в обоих сравниваемых периодах производится продукция одинакового
состава, используют в качестве весов индекса величину трудоемкости производства
единицы продукции в базисном периоде. Тогда индекс производительности труда по
трудовому методу рассчитывается по так называемой классической формуле:
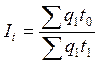 .
.
Данная
формула имеет широкое применение в экономических расчетах, т.к. разность ее
числителя и знаменателя непосредственно характеризует достигаемую экономию
(увеличение) фактических затрат труда вследствие изменения (роста или снижения)
его производительности:
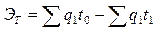 .
.
Стоимостной
индекс производительности труда:
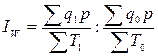 ,
,
где ∑q1p, ∑q0p – выработка продукции в единицу
времени (или на одного работающего) в стоимостном выражении в сопоставимых
ценах (р) соответственно в отчетном и
базисном периодах.
Стоимостной
индекс производительности труда позволяет анализировать производительность
труда всех работников предприятия, а не только рабочих.
Стоимостной
индекс производительности труда является основным индексом производительности
труда, в частности в промышленности. Он применяется для отдельных предприятий и
для совокупности предприятий.
Объективную
характеристику изменения эффективности труда за определенный период на
предприятии стоимостной индекс дает лишь при условии неизменности ассортимента
и структуры выпускаемой продукции. Соблюдение этих условий обеспечивает
тождественность стоимостного индекса производительности труда трудовому
индексу:
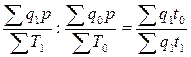 .
.
Рассмотренные
общие индексы производительности труда являются индексами переменного
состава. Поэтому как любой индекс переменного состава они отражают в
динамике средних уровней влияние двух факторов: изменение производительности
труда на отдельных участках, предприятиях и изменение доли (по числу
работающих) участков, предприятий с разным уровнем производительности труда.
Преобразуем
формулу натурального индекса производительности труда, для чего объем
представим как произведение выработки в единицу времени (W) на общие затраты труда (Т), т.е. q = W ∙ T.
Тогда
натуральный индекс производительности труда переменного состава будет
иметь вид:
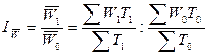 .
.
Обозначим
через 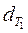 и
и 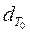 долю затрат рабочего
времени на производство продукции на данном предприятии в общих затратах рабочего
времени соответственно в отчетном и базисном периодах, т.е.:
долю затрат рабочего
времени на производство продукции на данном предприятии в общих затратах рабочего
времени соответственно в отчетном и базисном периодах, т.е.:
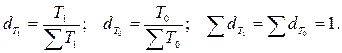
Тогда индекс
производительности труда переменного состава может быть выражен следующим
образом:
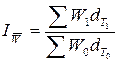 .
.
Чтобы
исключить влияние изменения структуры затрат на величину производительности
труда исчисляют индекс постоянного состава:
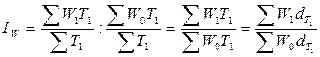 .
.
Индекс
постоянного состава можно получить, как показано выше и на основе
трудоемкости:
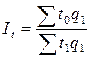 .
.
Два
индекса постоянного состава имеют различный экономический смысл. Первый индекс
дает возможность определить увеличение объема продукции за счет роста
производительности труда (∑W1T1 - ∑W0T1), а второй показывает, какая достигнута в этой связи
экономия в затратах труда (∑t0q1 - ∑t1q1).
Индекс
структурных сдвигов отражает изменение средней выработки за счет изменения
доли отработанного времени на отдельных предприятиях, имеющих разный уровень
производительности труда, в общих затратах рабочего времени:
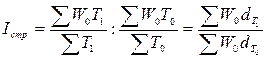 .
.
Названные
натуральные индексы производительности труда взаимосвязаны:
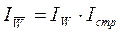 .
.
Разница
между числителем и знаменателем каждого из этих индексов показывает абсолютное
изменение выработки в отчетном периоде по сравнению с базисным за счет
указанных выше факторов.
3.3 Статистические
методы измерения влияния факторов роста производительности труда
Производительность труда – показатель
динамичный, постоянно изменяемый под воздействием множества факторов.
Все факторы, воздействующие на
производительность труда, можно разделить на две группы.
Первая
группа включает факторы, действующие в направлении повышения производительности
труда, улучшения организации труда и производства и социальных условий жизни
трудящихся.
Вторую
группу представляют факторы, негативно отражающиеся на производительности
труда. К ним относятся неблагоприятные природные условия, плохая организация
труда, напряженная социальная обстановка.
На
уровне отдельного предприятия или организации все факторы можно разделить на
внутренние и внешние.
Внутренние
факторы включают в себя уровень технической вооруженности предприятия,
эффективность применяемой технологии, энерговооруженность труда, организацию
производства, действенность применяемых систем стимулирования, обучение кадров
и повышение квалификации, улучшение структуры кадров и т.п., т.е. все, что
зависит от коллектива предприятия и его руководителей.
К
внешним факторам следует отнести изменения ассортимента продукции в связи с
изменением государственных заказов или спроса и предложения на рынке,
социально-экономические условия в обществе и регионе, уровень кооперации с
другими предприятиями, надежность материально-технического снабжения, природные
условия и т.п.
Измерение
влияния отдельных факторов дает возможность выявить резервы и перспективы роста
производительности труда. В статистике применяется три основных метода
измерения влияния отдельных факторов: индексный метод, метод группировок и
корреляционно-регрессионный анализ. Индексный метод применяется в тех случаях,
когда обобщающий показатель уровня или динамики анализируемого показателя можно
разложить на составляющие его субиндексы (факторы), т.е. на основе двух-,
трех-, четырехфакторных и т.д. индексных систем.
3.4 Построение
индексных моделей для изучения влияния динамики труда и отработанного времени
на изменение объема выпуска продукции
Рост производительности
труда является важнейшим фактором роста объема производства. Объем выпуска
продукции мультипликативно связан с производительностью труда и отработанным
временем. Следовательно, и между соответствующими им индексами существует
аналогичная взаимосвязь, т.е. имеет место следующая система взаимосвязанных
индексов, позволяющая осуществить факторный анализ динамики объема выпуска
продукции:
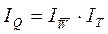 или
или 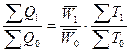 ,
,
где IQ
– индекс изменения объема произведенной продукции,
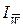 – индекс влияния изменения выработки на динамику объема
продукции (интенсивный фактор),
– индекс влияния изменения выработки на динамику объема
продукции (интенсивный фактор),
IQ – индекс влияния изменения
численности работающих на динамику объема продукции (экстенсивный фактор).
На
основе этой системы взаимосвязанных индексов можно исчислить общее изменение
объема выпуска продукции (∆Q) в абсолютном выражении как сумму
изменения объема продукции под влиянием производительности и численности
работников или отработанного ими времени:
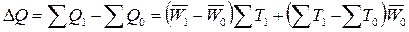 .
.
2. Расчетная
часть
Задание 1
Имеются следующие
выборочные данные по предприятиям одной из отраслей промышленности в отчетном
году (выборка 20%-ная механическая), млн. руб.:
|
№ организации п/п
|
Выпуск продукции,
млн. руб.
|
Среднесписочная
численность работников, чел.
|
Средняя стоимость
основных производственных фондов, млн. руб.
|
|
1
|
36,45
|
162
|
34,714
|
|
2
|
23,4
|
156
|
24,375
|
|
3
|
46,540
|
179
|
41,554
|
|
4
|
59,752
|
194
|
50,212
|
|
5
|
41,415
|
165
|
38,347
|
|
6
|
26,86
|
158
|
27,408
|
|
7
|
79,2
|
220
|
60,923
|
|
8
|
54,720
|
190
|
47,172
|
|
9
|
40,424
|
163
|
37,957
|
|
10
|
30,21
|
159
|
30,21
|
|
11
|
42,418
|
167
|
38,562
|
|
12
|
64,575
|
205
|
52,5
|
|
13
|
51,612
|
187
|
45,674
|
|
14
|
35,42
|
161
|
34,388
|
|
15
|
14,4
|
120
|
16,0
|
|
16
|
36,936
|
162
|
34,845
|
|
17
|
53,392
|
188
|
46,428
|
|
18
|
41,0
|
164
|
38,318
|
|
19
|
55,680
|
192
|
47,590
|
|
20
|
18,2
|
130
|
19,362
|
|
21
|
31,8
|
159
|
31,176
|
|
22
|
39,204
|
162
|
36,985
|
|
23
|
57,128
|
193
|
48,414
|
|
24
|
28,44
|
158
|
28,727
|
|
25
|
43,344
|
168
|
39,404
|
|
26
|
70,720
|
208
|
55,25
|
|
27
|
41,832
|
166
|
38,378
|
|
28
|
69,345
|
207
|
55,476
|
|
29
|
35,903
|
161
|
34,522
|
|
30
|
50,220
|
186
|
44,839
|
По исходным данным:
1. Постройте статистический ряд
распределения по признаку уровень производительности труда
(рассчитайте как отношение выпуска продукции к среднесписочной численности
работников), образовав пять групп с равными интервалами.
2. Постройте графики полученного ряда
распределения. Графически определите значения моды и медианы.
3. Рассчитайте характеристики
интервального ряда распределения: среднюю арифметическую, среднее
квадратическое отклонение, коэффициент вариации.
4. Вычислите среднюю арифметическую по
исходным данным, сравните ее с аналогичным показателем, рассчитанным в п. 3 для
интервального ряда распределения. Объясните причину их расхождения.
Сделайте выводы по
результатам выполнения задания.
Решение.
1. Построим статистический ряд
распределения по признаку уровень производительности труда,
для этого поделим выпуск продукции на среднесписочную численность работников
(табл. 2.1).
Таблица
2.1
Нахождение уровня производительности
труда
|
№ организации п/п
|
Выпуск продукции,
млн. руб.
|
Среднесписочная
численность работников, чел.
|
Уровень
производительности труда, тыс. руб.
|
|
1
|
36,45
|
162
|
225
|
|
2
|
23,4
|
156
|
150
|
|
3
|
46,540
|
179
|
260
|
|
4
|
59,752
|
194
|
308
|
|
5
|
41,415
|
165
|
251
|
|
6
|
26,86
|
158
|
170
|
|
7
|
79,2
|
220
|
360
|
|
8
|
54,720
|
190
|
288
|
|
9
|
40,424
|
163
|
248
|
|
10
|
30,21
|
159
|
190
|
|
11
|
42,418
|
167
|
254
|
|
12
|
64,575
|
205
|
315
|
|
13
|
51,612
|
187
|
276
|
|
14
|
35,42
|
161
|
220
|
|
15
|
14,4
|
120
|
120
|
|
16
|
36,936
|
162
|
228
|
|
17
|
53,392
|
188
|
284
|
|
18
|
41,0
|
164
|
250
|
|
19
|
55,680
|
192
|
290
|
|
20
|
18,2
|
130
|
140
|
|
21
|
31,8
|
159
|
200
|
|
22
|
39,204
|
162
|
242
|
|
23
|
57,128
|
193
|
296
|
|
24
|
28,44
|
158
|
180
|
|
25
|
43,344
|
168
|
258
|
|
26
|
70,720
|
208
|
340
|
|
27
|
41,832
|
166
|
252
|
|
28
|
69,345
|
207
|
335
|
|
29
|
35,903
|
161
|
223
|
|
30
|
50,220
|
186
|
270
|
Чтобы произвести
группировку, определим величину группировочного интервала по формуле:
i = (Xmax – Xmin) / n, где
Xmax, Xmin – соответственно максимальное и
минимальное значения уровня производительности труда,
n – число образуемых групп.
i = (360 – 120) / 5 = 48 тыс. руб.
Образуем
группы, которые отличаются друг от друга по уровню производительности труда на
эту величину:
I
120 – 168 тыс. руб.
II
168 – 216 тыс. руб.
III
216 – 264 тыс.руб.
IV
264 – 312 тыс. руб.
V
312 – 360 тыс. руб.
Группировку
организаций произведем в рабочей таблице (табл. 2.2).
Таблица
2.2
Группировка организаций по уровню
производительности труда
|
Группы
|
Группы организаций
по уровню производительности труда, тыс. руб.
|
Номер организации
|
Производительность
труда, тыс. руб.
|
|
I
|
120 – 168
|
2
15
20
|
150
120
140
|
|
|
3
|
-
|
|
II
|
168 – 216
|
6
10
21
24
|
170
190
200
180
|
|
|
4
|
-
|
|
III
|
216 – 264
|
1
3
5
9
11
14
16
18
22
25
27
29
|
225
260
251
248
254
220
228
250
242
258
252
223
|
|
|
12
|
-
|
|
IV
|
264 – 312
|
4
8
13
17
19
23
30
|
308
288
276
284
290
296
270
|
|
|
7
|
-
|
|
V
|
312 – 360
|
7
12
26
28
|
360
315
340
335
|
|
|
4
|
-
|
В
результате группировки получили следующий ряд распределения (табл. 2.3).
Таблица
2.3
Ряд распределения
|
Группы
|
Группы организаций
по уровню производительности труда, тыс. руб.
|
Число организаций
|
Накопленные
частоты, fнак
|
|
I
|
120 – 168
|
3
|
3
|
|
II
|
168 – 216
|
4
|
7
|
|
III
|
216 – 264
|
12
|
19
|
|
IV
|
264 – 312
|
7
|
26
|
|
V
|
312 – 360
|
4
|
30
|
2. Строим гистограмму (рис. 2.1).
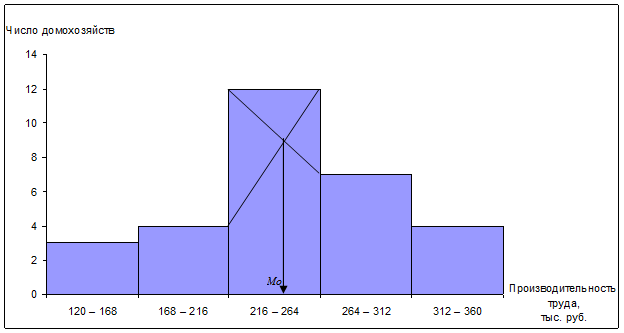
Рисунок 2.1.
Гистограмма полученного ряда
распределения. Нахождение моды
Из графика (рис.2.1) находим моду:
Мо ≈ 245 тыс. руб.
В данной совокупности чаще всего встречаются
организации с уровнем производительности труда 245 тыс. руб.
Строим график кумулята (рис. 2.2).

Рисунок
2.2. График
кумулята. Нахождение медианы
Из графика (рис. 2.2)
находим медиану:
Ме ≈ 250 тыс. руб.
В данной совокупности 50% организаций имеют
уровень производительности труда менее 250 тыс. руб., а остальные 50% - более
250 тыс. руб.
3. Расчет характеристик ряда
распределения представим в таблице 2.4.
Таблица
2.4
Расчет характеристик ряда распределения
|
Группы
|
Группы организаций
по уровню производительности труда, тыс. руб.
|
Число организаций, f
|
Хс
|
Xf
|
X -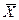 = = X- 248 = = X- 248
|
(X -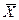 )2f )2f
|
|
I
|
120 – 168
|
3
|
144
|
432
|
-104
|
32448
|
|
II
|
168 – 216
|
4
|
192
|
768
|
-56
|
12544
|
|
III
|
216 – 264
|
12
|
264
|
3168
|
16
|
3072
|
|
IV
|
264 – 312
|
7
|
336
|
2352
|
88
|
54208
|
|
V
|
312 – 360
|
4
|
180
|
720
|
-68
|
18496
|
|
Итого
|
|
30
|
-
|
7440
|
-
|
120768
|
Среднюю
величину рассчитаем по формуле:
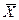 = ∑Xf / ∑f = 7440 / 30 = 248 тыс. руб.
= ∑Xf / ∑f = 7440 / 30 = 248 тыс. руб.
Дисперсия:
σ2
= 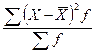 = 120768 / 30 =
4025,6.
= 120768 / 30 =
4025,6.
Среднее
квадратическое отклонение:
σ
=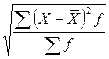 =
= 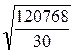 =
= 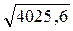 ≈ 63,448 тыс. руб.
≈ 63,448 тыс. руб.
Коэффициент
вариации:
V =
σ /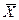 ∙ 100 = 63,448 / 248 ∙ 100 ≈
25,6%.
∙ 100 = 63,448 / 248 ∙ 100 ≈
25,6%.
Т.к. коэффициент вариации меньше 33%, то
совокупность считается однородной.
4. По исходным данным вычислим среднюю
арифметическую:
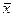 = ∑X / n = 7423 / 30 = 247,433 тыс. руб.
= ∑X / n = 7423 / 30 = 247,433 тыс. руб.
Полученная
средняя арифметическая отличается от аналогичного показателя, полученного в п.
3 для интервального ряда распределения, т.к. рассчитана по несгруппированным
данным и поэтому является более точной.
Задание 2
По исходным данным:
1. Установите наличие и характер связи
между признаками среднегодовая стоимость основных производственных фондов и уровень
производительности труда, образовав пять групп с равными
интервалами по обоим признакам, методами:
а) аналитической группировки,
б) корреляционной таблицы,
в) определите тесноту связи между
признаками, рассчитав коэффициент детерминации и эмпирическое корреляционное
отношение.
Решение
а) Аналитическая группировка
производится по факторному признаку. Обоснуем выбор факторного признака. Из
экономической теории известно, что размер предприятия, его мощность
определяются стоимостью основных производственных фондов (ОПФ), от величины
которых зависит производительность труда, следовательно, фоктор стоимости ОПФ
должен быть взят в основу группировки. Для того, чтобы произвести группировку,
вычислим величину группировочного интервала по формуле:
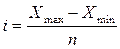 , где
, где
Xmax и Xmin – соответственно максимальное и минимальное значения
среднегодовой стоимости основных производственных фондов;
n – число образуемых групп (n = 5).
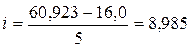 млн. руб.
млн. руб.
Образуем
группы, которые отличаются друг от друга по среднегодовой стоимости ОПФ на эту
величину;
I
16,0 – 24,985 млн. руб.
II
24,985 – 33,969 млн. руб.
III
33,969 – 42,954 млн.руб.
IV
42,954 – 51,938 млн. руб.
V
51,938 – 60,923 млн. руб.
Составляем
макет рабочей таблицы и проводим там группировку (табл. 2.5).
Таблица
2.5
Рабочая аналитическая таблица
|
Группы
|
Группы организаций
по среднегодовой стоимости основных производственных фондов, млн. руб.
|
Номер организации
|
Средняя стоимость
основных производственных фондов, млн. руб.
|
Уровень
производительности труда, тыс. руб.
|
|
I
|
16,0 – 24,985
|
2
15
20
|
24,375
16,0
19,362
|
150
120
140
|
|
|
3
|
59,737
|
410
|
|
II
|
24,985 – 33,969
|
6
10
21
24
|
27,408
30,21
31,176
28,727
|
170
190
200
180
|
|
|
4
|
117,521
|
740
|
|
III
|
33,969 – 42,954
|
1
3
5
9
11
14
16
18
22
25
27
29
|
34,714
41,554
38,347
37,957
38,562
34,388
34,845
38,318
36,985
39,404
38,378
34,522
|
225
260
251
248
254
220
228
250
242
258
252
223
|
|
|
12
|
447,974
|
2911
|
|
IV
|
42,954 – 51,938
|
4
8
13
17
19
23
30
|
50,212
47,172
45,674
46,428
47,590
48,414
44,839
|
308
288
276
284
290
296
270
|
|
|
7
|
330,329
|
2012
|
|
V
|
51,938 – 60,923
|
7
12
26
28
|
60,923
52,5
55,25
55,476
|
360
315
340
335
|
|
|
4
|
224,149
|
1350
|
|
Всего
|
30
|
1179,710
|
7423,0
|
На
основе рабочей таблицы составим сводную аналитическую таблицу (табл. 2.6).
Таблица
2.6
Сводная аналитическая таблица
|
Группы
|
Группы
организаций по среднегодовой стоимости основных производственных фондов, млн.
руб.
|
Число организаций
|
Средняя стоимость
основных производственных фондов, млн. руб.
|
Уровень
производительности труда, тыс. руб.
|
|
всего
|
на 1 органи-зацию, 
|
всего
|
на 1 органи-зацию, 
|
|
I
|
16,0 – 24,985
|
3
|
59,737
|
19,912
|
410
|
136,667
|
|
II
|
24,985 – 33,969
|
4
|
117,521
|
29,380
|
740
|
185,000
|
|
III
|
33,969 – 42,954
|
12
|
447,974
|
37,331
|
2911
|
242,583
|
|
IV
|
42,954 – 51,938
|
7
|
330,329
|
47,190
|
2012
|
287,429
|
|
V
|
51,938 – 60,923
|
4
|
224,149
|
56,037
|
1350
|
337,500
|
|
Всего
|
30
|
1179,710
|
39,324
|
7423
|
247,433
|
Сравнивая графы 5 и 7 аналитической таблицы,
мы видим, что с увеличением среднегодовой стоимости ОПФ растет и уровень
производительности труда, следовательно, между этими показателями имеется
прямая зависимость.
б) Составим рабочую корреляционную
таблицу (табл. 2.7). Для этого рассчитаем величину группировочного интервала
для уровня производительности труда по формуле:
i = (Ymax – Ymin) / n, где
Ymax, Ymin – соответственно максимальное и
минимальное значения уровня производительности труда;
n – число образуемых групп.
i = (360 – 120) / 5 = 48 тыс. руб.
Таблица
2.7
Рабочая корреляционная таблица
|
Средняя стоимость
основных производственных фондов, млн. руб.
|
Уровень
производительности труда, тыс. руб.
|
Всего
|
|
120
- 168
|
168
- 216
|
216
- 264
|
264
- 312
|
312
- 360
|
|
16,0 – 24,985
|
№2,
№15, №20
|
-
|
-
|
-
|
-
|
3
|
|
24,985 – 33,969
|
-
|
№6,
№10, №21, №24
|
-
|
-
|
-
|
4
|
|
33,969 – 42,954
|
-
|
-
|
№1,
№3, №5, №9, №11, №14, №16, №18, №22, №25, №27, №29
|
-
|
-
|
12
|
|
42,954 – 51,938
|
-
|
-
|
-
|
№4,
№8, №13, №17, №19, №23, №30
|
-
|
7
|
|
51,938 – 60,923
|
-
|
-
|
-
|
-
|
№7,
№12, №26, №28
|
4
|
|
Всего
|
3
|
4
|
12
|
7
|
4
|
30
|
На
основе рабочей корреляционной таблицы составляем итоговую корреляционную
таблицу (табл.2.8).
Таблица
2.8
Итоговая корреляционная таблица
|
Средняя стоимость
основных производственных фондов, млн. руб.
|
Уровень
производительности труда, тыс. руб.
|
Всего
|
|
 120
- 168 120
- 168
|
168
- 216
|
216
- 264
|
264
- 312
|
312
- 360
|
|
16,0 – 24,985
|
3
|
-
|
-
|
-
|
-
|
3
|
|
24,985 – 33,969
|
-
|
4
|
-
|
-
|
-
|
4
|
|
33,969 – 42,954
|
-
|
-
|
12
|
-
|
-
|
12
|
|
42,954 – 51,938
|
-
|
-
|
-
|
7
|
-
|
7
|
|
51,938 – 60,923
|
-
|
-
|
-
|
-
|
4
|
4
|
|
Всего
|
3
|
4
|
12
|
7
|
4
|
30
|
Т.к. распределение организаций произошло по
диагонали из левого верхнего угла в правый нижний угол таблицы, то связь между
признаками среднегодовая стоимость
основных производственных фондов и уровень
производительности труда прямая.
в) Коэффициент детерминации найдем по
формуле:
η2
= 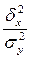 , где
, где
δ2х – межгрупповая дисперсия,
σ2y – общая дисперсия.
Межгрупповую
дисперсию найдем по формуле:
δ2х = ∑(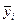 –
– 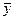 )2f
/ ∑f.
)2f
/ ∑f.
Расчет
межгрупповой дисперсии произведем в рабочей таблице (табл. 2.9).
Таблица
2.9
Рабочая таблица
|
Группы
|
Уровень
производительности труда в среднем на 1 организацию, yi
|
Число организаций, f
|
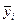 - - 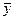 = = = = 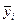 - 247,433 - 247,433
|
(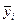 - - 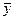 )2f )2f
|
|
I
|
136,667
|
3
|
-110,767
|
36807,763
|
|
II
|
185,000
|
4
|
-62,433
|
15591,684
|
|
III
|
242,583
|
12
|
-4,850
|
282,270
|
|
IV
|
287,429
|
7
|
39,995
|
11197,333
|
|
V
|
337,500
|
4
|
90,067
|
32448,018
|
|
∑
|
30
|
-
|
96327,069
|
δ2х = 96327,069 / 30 ≈
3210,902.
Общую
дисперсию находим по формуле:
σ2y = 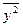 – (
– (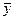 )2,
)2,
где 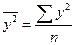 ;
; 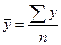 .
.
Расчет
среднего значения квадрата признака 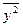 произведем в рабочей таблице (табл. 2.10).
произведем в рабочей таблице (табл. 2.10).
Таблица
2.10
Расчет среднего значения квадрата
признака 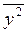
|
№ организации
|
Уровень
производительности труда, y
|
y2
|
|
1
|
225
|
50625
|
|
2
|
150
|
22500
|
|
3
|
260
|
67600
|
|
4
|
308
|
94864
|
|
5
|
251
|
63001
|
|
6
|
170
|
28900
|
|
7
|
360
|
129600
|
|
8
|
288
|
82944
|
|
9
|
248
|
61504
|
|
10
|
190
|
36100
|
|
11
|
254
|
64516
|
|
12
|
315
|
99225
|
|
13
|
276
|
76176
|
|
14
|
220
|
48400
|
|
15
|
120
|
14400
|
|
16
|
228
|
51984
|
|
17
|
284
|
80656
|
|
18
|
250
|
62500
|
|
19
|
290
|
84100
|
|
20
|
140
|
19600
|
|
21
|
200
|
40000
|
|
22
|
242
|
58564
|
|
23
|
296
|
87616
|
|
24
|
180
|
32400
|
|
25
|
258
|
66564
|
|
26
|
340
|
115600
|
|
27
|
252
|
63504
|
|
28
|
335
|
112225
|
|
29
|
223
|
49729
|
|
30
|
270
|
72900
|
|
∑
|
1938297
|
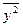 =
1938297,0 / 30 ≈ 64609,90;
=
1938297,0 / 30 ≈ 64609,90;
σ2y = 64609,90 - 247,4332
≈ 3386,646;
η2
= 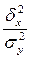 = 3210,902 / 3386,646
≈ 0,948 или 94,8%.
= 3210,902 / 3386,646
≈ 0,948 или 94,8%.
Вариация уровня производительности труда на 94,8% обусловлена вариацией среднегодовой стоимости основных
производственных фондов.
Эмпирическое
корреляционное отношение находим по формуле:
η
= 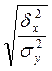 ≈ 0,974.
≈ 0,974.
Т.к. эмпирическое корреляционное отношение
> 0,9, то можно сделать вывод, что связь между среднегодовой стоимостью ОПФ и уровнем
производительности труда весьма тесная.
Задание 3
По
результатам выполнения задания 1 с вероятностью 0,954 определите:
1. Ошибку выборки среднего уровня
производительности труда и границы, в которых будет находиться производительность
труда в генеральной совокупности.
2. Ошибку выборки доли организаций с
уровнем производительности труда 264 тыс. руб. и более и границы, в которых
будет находиться генеральная доля.
Решение.
1. При расчете характеристик ряда
распределения в задании 1 получили:
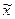 = 248 тыс. руб.;
= 248 тыс. руб.;
σ2
= 4025,60;
n = 30;
выборка
20%-ная => N = 150.
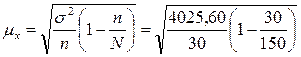 ≈ 10,361 тыс. руб.;
≈ 10,361 тыс. руб.;
P = 0,954 => t = 2;
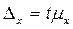 = 2 ∙ 10,361 = 20,722 тыс. руб.
= 2 ∙ 10,361 = 20,722 тыс. руб.
Нижнюю
и верхнюю границы интервала определим по формуле:
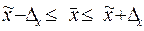 .
.
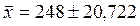 ;
;  [227,278; 268,722].
[227,278; 268,722].
С вероятностью 0,954 можно утверждать, что
ошибка выборки среднего уровня производительности труда составит 20,722 тыс.
руб., и средний уровень производительности труда в генеральной совокупности
будет находиться в пределах от 277,278 тыс. руб. до 268,722 тыс. руб.
2. Долю организаций с уровнем
производительности труда 264 тыс. руб. и более находим по формуле:
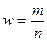 , где
, где
m – число организаций с уровнем
производительности труда 264 тыс. руб. и более;
n – число наблюдений (n = 30).
Получаем:
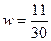 =0,367 или 36,7%
=0,367 или 36,7%
Находим
среднюю ошибку:
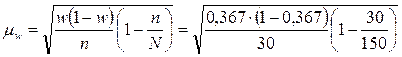 ≈ 0,079 или 7,9%;
≈ 0,079 или 7,9%;
P = 0,954 => t = 2;
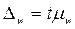 = 2 ∙ 0,079 = 0,157 или 15,7%.
= 2 ∙ 0,079 = 0,157 или 15,7%.
Нижнюю
и верхнюю границы интервала определим по формуле:
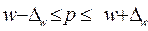 .
.
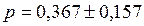 ;
; 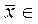 [0,209; 0,524] или [20,9%; 52,4%].
[0,209; 0,524] или [20,9%; 52,4%].
С вероятностью 0,954 можно утверждать, что ошибка выборки
доли организаций с уровнем производительности труда 264 тыс. руб. и более
составит 36,7%, и генеральная доля будет находиться в пределах от 20,9% до
52,4%.
Задание 4
Имеются
следующие данные по организациям за два года:
|
Показатели
|
Базисный год
|
Отчетный год
|
|
Выпуск продукции (в сопоставимых ценах), млн. руб.
|
40,8
|
54,2
|
|
Среднесписочная численность работников, чел.
|
164
|
180
|
|
В том числе рабочих, чел.
|
130
|
145
|
|
Отработано рабочими человеко-дней
|
31 200
|
33 060
|
|
Отработано рабочими человеко-часов
|
240 240
|
261 174
|
Определите:
1. Уровни среднечасовой, среднедневной и
среднегодовой производительности труда, их динамику и взаимосвязь. Расчеты
представьте в таблице.
2. Абсолютный прирост среднегодовой
производительности труда одного работника за счет отдельных факторов
(среднечасовой производительности труда рабочего, средней продолжительности
рабочего дня и рабочего года, доли рабочих в общей численности работников).
Сделайте выводы.
Решение.
1. Средняя часовая выработка отражает
результаты труда одного рабочего за час фактической работы. Она равна отношению
объема произведенной продукции к числу человеко-часов, фактически отработанных
в течение данного периода времени.
Средняя дневная выработка
равна отношению объема произведенной продукции к числу человеко-дней,
фактически отработанных всеми рабочими предприятиями.
Средняя выработка за
период времени (среднемесячная, среднеквартальная, среднегодовая) одного
списочного рабочего или работника всего персонала, непосредственно связанного с
производством данной продукции (промышленно-производственного персонала) равна
отношению объема продукции к среднесписочной численности рабочих (ТР)
или работников промышленно-производственного персонала (ТППП)
соответственно.
Расчет вышеперечисленных
средних уровней производительности труда представлен в таблице 2.11:
Таблица
2.11
Нахождение средних уровней
производительности труда
|
Показатели
|
Базисный год
|
Отчетный год
|
|
Выпуск продукции (в сопоставимых ценах), млн. руб.
|
40,8
|
54,2
|
|
Среднесписочная численность работников, чел.
|
164
|
180
|
|
В том числе рабочих, чел.
|
130
|
145
|
|
Отработано рабочими человеко-дней
|
31 200
|
33 060
|
|
Отработано рабочими человеко-часов
|
240 240
|
261 174
|
|
Средняя часовая выработка, тыс. руб.
|
0,170
|
0,208
|
|
Средняя дневная выработка, тыс. руб.
|
1,308
|
1,639
|
|
Средняя выработка за год на одного рабочего, тыс. руб.
|
313,846
|
373,793
|
|
Средняя выработка за год на одного списочного работника,
тыс. руб.
|
248,780
|
301,111
|
Динамику показателей
рассчитаем при помощи индекса:
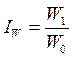 ,
,
где W1 и W0 – уровни соответствующей производительности труда в
отчетном и базисном периодах соответственно.
1) Динамика средней часовой выработки:
I = 0,208 / 0,170
= 1,222 или 122,2%
Средняя часовая выработка в отчетном году по сравнению с
базисным увеличилась на 22,2%.
2) Динамика средней дневной выработки:
I = 1,639 / 1,308
= 1,254 или 125,4%
Средняя дневная выработка в отчетном году по сравнению с
базисным увеличилась на 25,4%.
3) Динамика средней выработки за год
одного рабочего:
I = 373,793 / 313,846
= 1,191 или 119,1%
Среднегодовая выработка на одного рабочего в отчетном году по
сравнению с базисным увеличилась на 19,1%.
4) Динамика средней выработки за год
одного списочного работника:
I = 301,111 / 248,780
= 1,210 или 121,0%
Среднегодовая выработка на одного списочного работника в
отчетном году по сравнению с базисным увеличилась на 21,0%.
Между
рассчитанными показателями существуют следующие взаимосвязи:
Средняя дневная выработка
= Средняя часовая выработка × Средняя продолжительность рабочего дня;
Средняя
годовая выработка на одного рабочего = Средняя дневная выработка ×
Средняя продолжительность рабочего года;
Средняя
годовая выработка одного работника = Средняя годовая выработка одного рабочего
× Доля рабочих в общей численности работающих.
Средняя
продолжительность рабочего дня равна отношению отработанных человеко-часов к
отработанным человеко-дням.
Средняя
продолжительность рабочего года равна отношению отработанных человеко-дней к
численности рабочих.
Доля
рабочих в общей численности работающих равна отношению численности работников к
среднесписочной численности работников.
Расчет
этих показателей представим в таблице 2.12:
Таблица
2.12
Рабочая таблица
|
Показатели
|
Базисный год
|
Отчетный год
|
|
Средняя продолжительность рабочего дня, ч
|
7,7
|
7,9
|
|
Средняя продолжительность рабочего года, дн.
|
240
|
228
|
|
Доля рабочих в общей численности работающих
|
0,793
|
0,806
|
2. Запишем формулу среднегодовой
производительности одного рабочего:
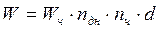 ,
,
где W –
среднегодовая производительность труда одного работника,
Wч – среднечасовая производительность
труда (выработка) рабочего,
nдн – средняя продолжительность рабочего
дня,
nг - средняя продолжительность рабочего
года,
d – доля рабочих в общей численности работников.
Тогда
абсолютный прирост среднегодовой производительности труда одного работника за
счет изменения среднечасовой производительности труда рабочего:
ΔW (Wч) = Wч1∙ nдн1∙ nг1∙ d1 - Wч0∙ nдн1∙ nг1∙ d1 = 0,208 ∙ 7,9 ∙ 228 ∙ 0,806 - 0,170
× × 7,9 ∙ 228 ∙ 0,806 = 54,693 тыс. руб.
Среднегодовая производительность труда
одного работника в отчетном году по сравнению с базисным годом увеличилась на
54,693 тыс. руб. за счет изменения среднечасовой производительности труда
рабочего.
Абсолютный
прирост среднегодовой производительности труда одного работника за счет
изменения средней продолжительности рабочего дня:
ΔW (nдн) = Wч0∙ nдн1∙ nг1∙ d1 - Wч0∙ nдн0∙ nг1∙ d1 = 0,170 ∙ 7,9 ∙ 228 ∙ 0,806 - 0,170
× × 7,7 ∙ 228 ∙ 0,806 = 6,238 тыс. руб.
Среднегодовая производительность труда
одного работника в отчетном году по сравнению с базисным годом увеличилась на
6,238 тыс. руб. за счет изменения средней продолжительности рабочего дня.
Абсолютный прирост
среднегодовой производительности труда одного работника за счет изменения
средней продолжительности рабочего года:
ΔW (nг) = Wч0∙ nдн0∙ nг1∙ d1 - Wч0∙ nдн0∙ nг0∙ d1 = 0,170 ∙ 7,7 ∙ 228 ∙ 0,806 - 0,170
×
× 7,7 ∙ 240 ∙ 0,806 = -12,641 тыс. руб.
Среднегодовая производительность труда одного работника в
отчетном году по сравнению с базисным годом уменьшилась на 12,641 тыс. руб. за
счет изменения средней продолжительности рабочего года.
Абсолютный прирост
среднегодовой производительности труда одного работника за счет изменения доли
рабочих в общей численности работников:
ΔW (d) = Wч0∙ nдн0∙ nг0∙ d1 - Wч0∙ nдн0∙ nг0∙ d0 = 0,170 ∙ 7,7 ∙ 240 ∙ 0,806 - 0,170
×
× 7,7 ∙ 240 ∙ 0,793 = 4,040 тыс. руб.
Среднегодовая производительность труда одного работника в
отчетном году по сравнению с базисным годом увеличилась на 4,040 тыс. руб. за
счет изменения доли рабочих в общей численности работников.
Взаимосвязь абсолютных
приростов:
ΔW (Wч;
nдн; nг; d) = ΔW (Wч) + ΔW (nдн) + ΔW (nг) + ΔW (d)
54,693 + 6,238 - 12,641 + 4,040 =
52,331.
Среднегодовая производительность труда одного работника в
отчетном году по сравнению с базисным годом увеличилась на 52,331 тыс. руб. за
счет изменения всех факторов.
3. Аналитическая
часть
3.1 Постановка
задачи:
Одним из направлений
изучения производительности труда является анализ средней выработки продукции,
полученной за несколько отчетных периодов, т.е. ее динамики.
Имеются данные об объеме
промышленной продукции и среднегодовой численности за несколько лет,
представленные в табл. 3.1, на основе которых находится среднегодовая производительность
труда как их отношение.
Таблица 3.3.1
Нахождение среднегодовой
производительности труда**
|
Год
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
Объем промышленной
продукции, млрд. руб.
|
4763
|
5881
|
6868
|
8498
|
11209
|
|
Среднегодовая
численность
промышленно-производственного
персонала, тыс. человек
|
13294
|
13282
|
12886
|
12384
|
11977
|
|
Среднегодовая
производительность труда, тыс. руб.
|
358,282
|
442,780
|
532,982
|
686,208
|
935,877
|
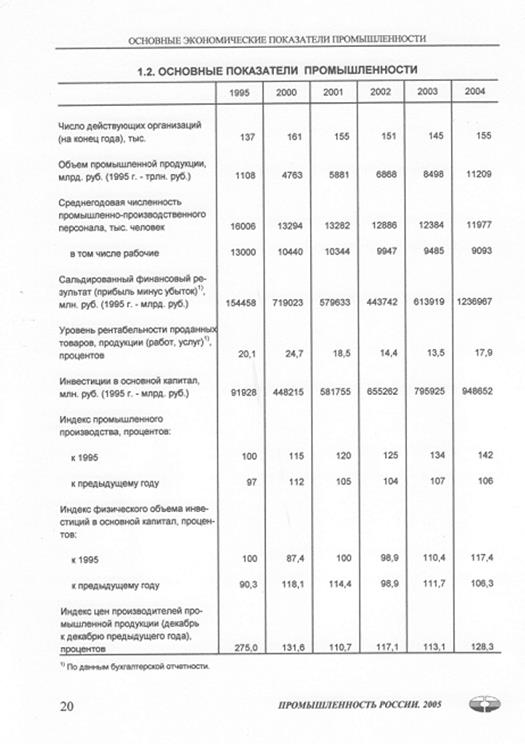
**Построено
по данным табл. «Основные показатели промышленности», источник: Промышленность
России, 2005: Стат.сб./Росстат. – М. – 2006. – с.20.
По
данным, представленным в табл. 3.1 проведем анализ динамики среднегодовой
производительности труда, для чего рассчитаем следующие показатели:
·
абсолютный
прирост;
·
темп
роста;
·
темп
прироста;
·
абсолютное
значение 1% прироста;
·
средние
за период уровень ряда, абсолютный прирост, темпы роста и прироста.
3.2 Методика
решения задачи
Расчет показателей
анализа рядов динамики осуществим по формулам, представленным в табл. 3.2.
Таблица 3.2
Формулы расчета показателей
|
Показа-тель
|
Базисный
|
Цепной
|
Средний
|
|
Абсолют-
ный прирост
|
∆бу
= yi – y1 (1)
|
∆цу
= yi – yi-1 (2)
|
 ∆у
= (yn – y1)/(n – 1) (3) ∆у
= (yn – y1)/(n – 1) (3)
|
|
Темп
роста
|
Tбр = yi/y1× 100 (4)
|
Tцр = yi/ yi-1× 100 (5)
|
 
Tр = n – 1√yn/y1× 100 (6)
|
|
Темп
прироста
|
Tб∆ = Tбр – 100 (7)
|
Tц∆ = Tцр – 100 (8)
|
  T∆
= Tр – 100 (9) T∆
= Tр – 100 (9)
|
Средний
уровень в интервальном ряду динамики вычисляется по формуле: n
 y = ∑ yi/n.
(10)
y = ∑ yi/n.
(10)
i=1
Для
определения абсолютной величины, стоящей за каждым процентом прироста среднегодовой
производительности труда, рассчитывают показатель абсолютного значения 1%
прироста (А%). Один из способов его
расчета – расчет по формуле:
А%i = yi-1/100.
(11)
Числовые
обозначения:
y1 – уровень первого периода; yi – уровень сравниваемого периода; yi-1 – уровень предыдущего периода; yn – уровень последнего периода; n – число уровней ряда динамики.
3.3
Технология выполнения компьютерных расчетов
Расчеты показателей
анализа динамики среднегодовой производительности труда выполнены с применением
пакета прикладных программ обработка электронных таблиц MS Excel в среде Window XP.
Расположение на рабочем
листе Excel исходных данных (табл.3.1) и
расчетных формул (1)-(11) (в формате Excel) представлено в табл.3.3.
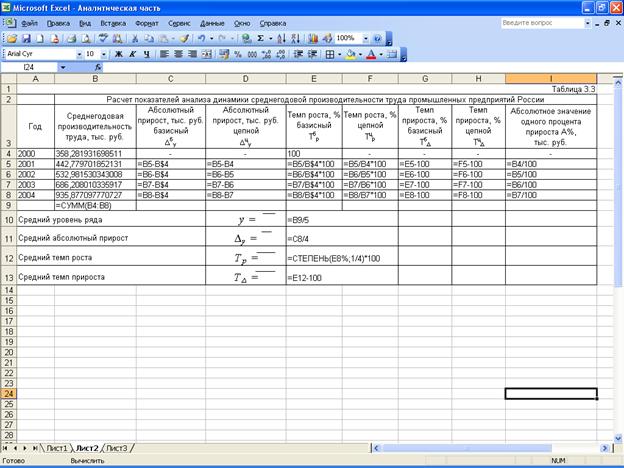
Результаты
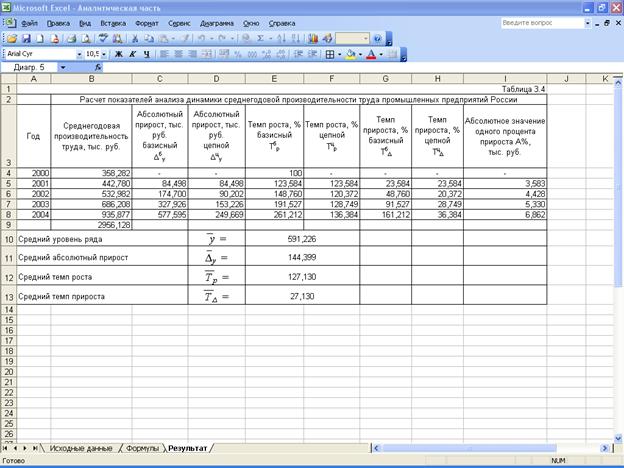
расчетов приведены в табл. 3.4.
На
рис.3.1 представлено графическое изображение динамики среднегодовой
производительности труда промышленных предприятий России за 5 лет.
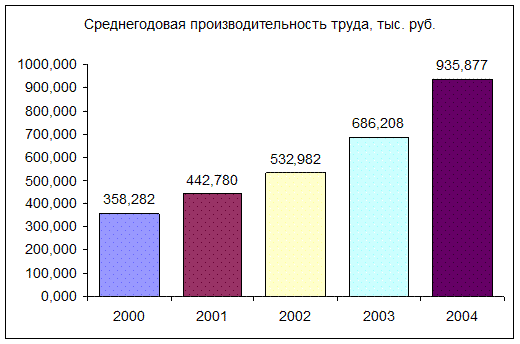
Рис. 3.1. Диаграмма динамики среднегодовой
производительности труда промышленности
3.4 Анализ
результатов статистических компьютерных расчетов
Результаты проведенных
расчетов позволяют сделать следующие выводы.
Сумма среднегодовой
производительности труда промышленных предприятий России выросла на 161,2%, что
в абсолютном выражении составляет 577,595 тыс. руб.
Наблюдается положительная
динамика в течение всего периода. Она носит не скачкообразный, а планомерный
характер. Об этом говорят цепные абсолютные приросты (от года к году они
увеличиваются, что свидетельствует об абсолютном ускорении изменения). Это же
подтверждает и графическое изображение динамики среднегодовой
производительности труда промышленных предприятий (см. рис.3.1).
В течение анализируемого
пятилетнего периода средний размер среднегодовой производительности труда составил
591,226 тыс. руб., в среднем за год она увеличивалась на 144,399 тыс. руб. (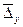 = 144,399 ) или на 27,1%
(
= 144,399 ) или на 27,1%
(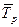 = 127,1%).
= 127,1%).
Ускоренный рост среднегодовой
производительности труда промышленности можно увидеть и по увеличивающемуся
абсолютному значению 1% прироста.
Для более глубокого
анализа динамики производительности труда необходимо изучить изменения
составляющих их элементов и направления этих изменений за рассматриваемый
период, выявить влияние отдельных факторов.
Заключение
Из всего выше написанного
можно сделать вывод: задачами статистики производительности труда являются
разработка методов определения производительности труда, нахождения ее уровня,
определение динамики производительности труда, выявление влияния различных
факторов на динамику производительности труда, изучение влияния динамики труда
и отработанного времени на изменение объема выпуска продукции.
По
результатам расчетной части работы можно сделать следующие выводы:
Задание
1
Наибольшее
число организаций – 12 из 30 (40%) попадают в группы с уровнем производительности
труда от 216 до 264 тыс. руб.
В
данной совокупности чаще всего встречаются организации с уровнем
производительности труда 245 тыс. руб.
В изучаемой совокупности
50% организаций имеют уровень производительности труда менее 250 тыс. руб., а
остальные 50% - более 250 тыс. руб.
Среднее значение уровня
производительности труда составило 248 тыс. руб.
Т.к. коэффициент вариации
меньше 33%, то совокупность считается однородной.
Полученная по исходным
данным средняя арифметическая меньше аналогичного показателя, полученного по
сгруппированным данным, т.к. рассчитана по несгруппированным данным и поэтому
является более точной.
Задание 2
Сравнивая графы 5 и 7
аналитической таблицы, мы видим, что с увеличением среднегодовой стоимости ОПФ
растет и уровень производительности труда, следовательно, между этими
показателями имеется прямая зависимость.
Т.к. распределение
организаций произошло по диагонали из левого верхнего угла в правый нижний угол
таблицы, то связь между признаками среднегодовая стоимость основных производственных
фондов и уровень производительности труда прямая.
Вариация уровня
производительности труда на 94,8% обусловлена вариацией среднегодовой стоимости
основных производственных фондов.
Т.к. эмпирическое
корреляционное отношение > 0,9, то можно сделать вывод, что связь между
среднегодовой стоимостью ОПФ и уровнем производительности труда весьма тесная.
Задание 3
С вероятностью 0,954
можно утверждать, что ошибка выборки среднего уровня производительности труда
составит 20,722 тыс. руб., и средний уровень производительности труда в
генеральной совокупности будет находиться в пределах от 277,278 тыс. руб. до
268,722 тыс. руб.
С вероятностью 0,954
можно утверждать, что ошибка выборки доли организаций с уровнем
производительности труда 264 тыс. руб. и более составит 36,7%, и генеральная
доля будет находиться в пределах от 20,9% до 52,4%.
Задание 4
Средняя часовая выработка в отчетном
году по сравнению с базисным увеличилась на 22,2%.
Средняя дневная выработка
в отчетном году по сравнению с базисным увеличилась на 25,4%.
Среднегодовая выработка
на одного рабочего в отчетном году по сравнению с базисным увеличилась на
19,1%.
Среднегодовая выработка
на одного списочного работника в отчетном году по сравнению с базисным
увеличилась на 21,0%.
Среднегодовая производительность
труда одного работника в отчетном году по сравнению с базисным годом
увеличилась на 54,693 тыс. руб. за счет изменения среднечасовой
производительности труда рабочего.
Среднегодовая
производительность труда одного работника в отчетном году по сравнению с
базисным годом увеличилась на 6,238 тыс. руб. за счет изменения средней
продолжительности рабочего дня.
Среднегодовая
производительность труда одного работника в отчетном году по сравнению с
базисным годом уменьшилась на 12,641 тыс. руб. за счет изменения средней
продолжительности рабочего года.
Среднегодовая
производительность труда одного работника в отчетном году по сравнению с
базисным годом увеличилась на 4,040 тыс. руб. за счет изменения доли рабочих в
общей численности работников.
Среднегодовая
производительность труда одного работника в отчетном году по сравнению с
базисным годом увеличилась на 52,331 тыс. руб. за счет изменения всех факторов.
По результатам
аналитической части можно сделать следующие выводы:
Сумма среднегодовой производительности
труда промышленных предприятий России выросла на 161,2%, что в абсолютном
выражении составляет 577,595 тыс. руб.
В течение анализируемого
пятилетнего периода средний размер среднегодовой производительности труда
составил 591,226 тыс. руб., в среднем за год она увеличивалась на 144,399 тыс.
руб. (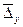 = 144,399) или на
27,1% (
= 144,399) или на
27,1% (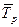 = 127,1%).
= 127,1%).
Список литературы
1. Васильева Э.К. Статистика: учеб. для
студентов вузов, обучающихся по специальностям экономики и управления (080100)
/ Э.К. Васильева, В.С. Лялин. – М.: ЮНИТИ-ДАНА, 2007. – 399с.
2. Гусаров, В.М. Статистика: учеб.
пособие для вузов / В.М. Гусаров. – М.: ЮНИТИ-ДАНА, 2001. – 463с.
3. Гусаров, В.М. Теория статистики:
учеб. пособие для вузов / В.М. Гусаров. – М.: Аудит, ЮНИТИ, 1998. – 247с.
4. Экономика и статистика фирм: учеб. /
В.Е. Адамов, С.Д. Ильенкова, Т.П. Сиротина, С.А. Смирнов; под ред. д-ра экон.
наук, проф. С.Д. Ильенковой. – 3-е изд., перераб. и доп. – М.: Финансы и
статистика, 2000. – 228 с.: ил.
5. Промышленность России, 2005:
Стат.сб./Росстат. – М. – 2006. – С.20.
6. Тульский статистический ежегодник,
2006: Стат. сб. – Тула: Туластат. – 2007. – С.131.
7. Официальный сайт Госкомстата РФ: www.gks.ru
Приложение