Вариант 1

     Задача 1.1.

В таблице приведено положение команд НХЛ Тихоокеанского дивизиона на 15.11.2001 и 15.01.2002 гг.

Тихоокеанский дивизион НХЛ (промежуточные результаты)

Команда	Очки на 15.11.01	Очки на 15.01.02
Эдмонтон	30	46
Ванкувер	28	42
Анахайм	27	39
Колорадо	25	62
Лос-Анжелес	21	41
Калгари	19	40
Сан-Хосе	17	37

Определите уровень согласованности промежуточных результатов первенства дивизиона с помощью коэффициентов ранговой корреляции. Сделайте выводы.

Решение.

Составляем расчетную таблицу:

Команда	Очки на 15.11.01 R1	Очки на 15.01.02 R2	Разность рангов d	d2	Баллы для рангов
Положи- тельные Q	Отрица- тельные Р	Итого
Сан-Хосе	1	1	0	0	6	0	6
Калгари	2	4	-2	4	3	2	1
Лос-Анжелес	3	5	-2	4	2	2	0
Колорадо	4	7	-3	9	0	1	-1
Анахайм	5	2	3	9	0	0	0
Ванкувер	6	3	3	9	0	0	0
Эдмонтон	7	6	1	1	0	0	0
Итого				36	11	5	6

Коэффициент ранговой корреляции Спирмена рассчитывается по формуле:    .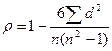

Получаем:   .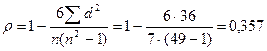

Коэффициент ранговой корреляции Кендэлла рассчитывается по формуле: .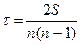

Получаем:     .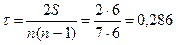

Вывод:

Так как коэффициенты ранговой корреляции близки к нулю, то уровень согласованности промежуточных результатов первенства дивизиона достаточно низкий.

Задача 1.2.

Проведено обследование продолжительности беременности женщин

Продолжительность беременности в днях	Число обследованных женщин
257	10
258	20
259	20
260	40
261	40
262	60
263	70
264	100
265	120
266	100
267	100
268	70
269	100
270	50
271	40
272	40
273	10
274	5
275	5
Всего	1000

Является ли данное распределение нормальным, проверьте соответствие теоретическому закону распределения с помощью критерия хи-квадрат.

Решение.

Определим . 

Для нахождения теоретических частот нормального распределения составляем расчетную таблицу.

х	fфакт	x* fфакт	x2 * fфакт	t	f(t)	fтеор
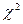
257	10	2570	660490	-2,40	0,0224	6	2,41725
258	20	5160	1331280	-2,12	0,0422	12	6,12619
259	20	5180	1341620	-1,85	0,0721	20	0,00241
260	40	10400	2704000	-1,57	0,1163	32	2,05204
261	40	10440	2724840	-1,30	0,1714	47	1,0496
262	60	15720	4118640	-1,02	0,2371	65	0,3922
263	70	18410	4841830	-0,75	0,3011	83	1,92491
264	100	26400	6969600	-0,48	0,3555	98	0,06227
265	120	31800	8427000	-0,20	0,391	107	1,50937
266	100	26600	7075600	0,07	0,398	109	0,77442
267	100	26700	7128900	0,35	0,3752	103	0,08399
268	70	18760	5027680	0,62	0,3292	90	4,57145
269	100	26900	7236100	0,90	0,2661	73	9,97969
270	50	13500	3645000	1,17	0,2012	55	0,49012
271	40	10840	2937640	1,44	0,1415	39	0,03574
272	40	10880	2959360	1,72	0,0909	25	9,09484
273	10	2730	745290	1,99	0,054	15	1,56519
274	5	1370	375380	2,27	0,0303	8	1,32043
275	5	1375	378125	2,54	0,0158	4	0,10204
Всего	1000	265735	70628375				43,5542

С помощью таблицы получаем:      

,

.

,     .

, 

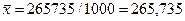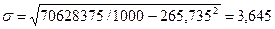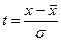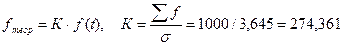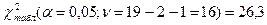
Так как 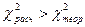, то распределение не является нормальным.

Задача 1.3.

1.                С помощью коэффициентов сопряженности ответьте на вопрос: являются ли «конфликтные ситуации» фактором гипертонической болезни?

2.                      Рассчитайте по этой таблице сопряженности коэффициент нормированной информации.

Конфликтные си- туации на работе	Больные гипертонией	Здоровые	Всего
Есть	28	7	35
Нет	17	38	55
Итого	45	45	90

Решение.

Рассчитаем коэффициент контингенции и коэффициент ассоциации по формулам:

,       .

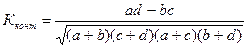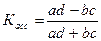Расчетная таблица:

Конфликтные си- туации на работе	Больные гипертонией	Здоровые	Всего
Есть	28(a)	7(b)	35(a+b)
Нет	17(c)	38(d)	55(c+d)
Итого	45(a+c)	45(b+d)	90

Коэффициент контингенции: .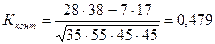

Коэффициент ассоциации: .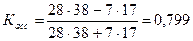

Рассчитанные коэффициенты свидетельствуют о заметной связи между  «конфликтными ситуациями» и гипертонической болезнью.

Задача 1.4.

По данным, полученным в результате обследования работников завода «Электросигнал»:

1.                С помощью критерия хи-квадрат при 5% уровне значимости проверьте гипотезу о наличии взаимосвязи между видом заболевания и его продолжительностью.

2.                Оцените тесноту связи с помощью коэффициентов сопряженности Пирсона, Чупрова, Крамера. Рассчитайте также скорректированный коэффициент Пирсона.

Количество дней нетрудо- способности за год	Бо- лез- ни нер- вов	Гипер- тони- ческая бо- лезнь	Хрони- ческие заболе- вания органов дыхания	Бо- лезни почек	Жен- ские болез- ни	Ос- тео- хонд- роз	Все- го
До 5	7	5	21	9	12	12	66
6-10	10	11	19	19	13	12	84
11-15	6	18	11	3	14	11	63
16-20	5	12	7	5	9	5	43
21-25	4	4	1	4	1	4	18
26-30	0	10	1	1	0	7	19
31-35	3	3	3	0	2	5	16
36 и более	4	18	2	3	0	9	36
Итого	39	81	65	44	51	65	345

Решение.

1. Проверяем условие: 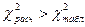, где  .

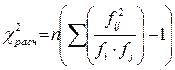Получаем: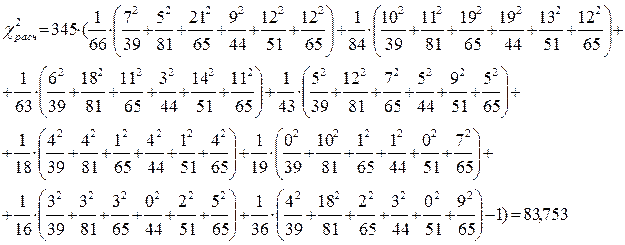

.

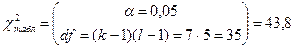Так как 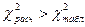, то вид заболевания можно считать фактором ее продолжительности.

2.Коэффициент взаимной сопряженности Пирсона:

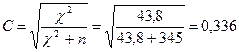
 Коэффициент взаимной сопряженности Чупрова:

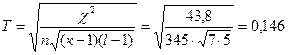
 Коэффициент взаимной сопряженности Крамера:

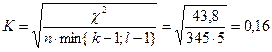
Скорректированный коэффициент Пирсона:

,   ,   .

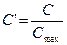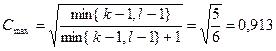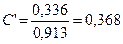Таким образом, между видом заболевания и его продолжительностью существует заметная связь.