Логическая операция, посредством которой из некото­рого количества исходных суждений получается новое суж­дение, определенным образом связанное с исходными, на­зывается умозаключением. Например: Все товары обладают потребительной и меновой стоимостью. Нефть — товар. Нефть обладает потребительной и меновой стоимостью.

Это одна из распространенных форм умозаключения. Его структура включает в себя посылки /два первых сужде­ния/, заключение /третье суждение/ и логическую связь между посылками и заключением /она подразумевается/.

Достоинства умозаключений в том, что они позволяют получать новые знания, не прибегая всякий раз к опыту. Однако при условии, что исходные суждения истинны и способы построения умозаключений, которыми пользуем­ся, соответствуют правилам логики. Вряд ли, к примеру, можно получить какой-либо вывод из суждений, между ко­торыми нет логической связи: «Все металлы электропроводны» и «Ни одна планета не светит собственным светом», «В огороде бузина» и «В Киеве дядька».

Деление умозаключений на определенные виды обус­ловлено формой их построения, т. с. типом получения но­вого, выводного знания. Индуктивное умозаключение, нап­ример, позволяет делать вывод от частного, единичного знания к общему; от посылок, выражающих знания мень­шей степени общности, к заключению со знанием большей степени общности. Дедуктивное умо­заключение, напротив, позволяет заключить от общего зна­ния к частному, т. е. от посылок, выражающих знания боль­шей степени общности, к заключению со знанием меньшей степени общности.

Каждый из названных видов умозаключений в свою очередь делится на подвиды. В зависимости от количества используемых посылок, из которых строится вывод, дедуктивные умозаключения бывают непосредственные и опосредствованные.

Целью данной работы является изучение непосредственных умозаключений и их видов.

1. Понятие непосредственных умозаключений

Логика допускает возможность сделать опреде­ленный вывод даже из одной посылки, из одного простого атрибутивного суждения. В нем, как известно, зафиксиро­вана связь двух понятий, именуемых субъектом и предика­том. В силу этого в простом суждении есть информация явная, лежащая, как говорится, на поверхности, и неявная, которую можно извлечь из суждения, подвергнув его неко­торым преобразованиям. Именно эта операция называется непосредственным умозаключением, т.е. дедуктивным вы­водом, делаемым из одной посылки.

Допустим, исходным суждением является: «Все менед­жеры — предприниматели». Содержащаяся в нем информа­ция такова, что можно сделать вывод: «Ни один менеджер не является не предпринимателем». Если истинно первое суждение, то истинным, надо полагать, будет и второе. Суть этой операции в превращении одного суждения в другое. Превращение суждения — такая логическая операция, ког­да из данного суждения получается равнозначное ему, но противоположное по качеству. Исходное суждение было ут­вердительным, полученное в результате превращения стало 'отрицательным. Чтобы превратить суждение, нужно изме­нить связку на противоположную, а предикат — на проти­воречащее понятие. Разнообразные виды суждений имеют обобщенную схему их превращений[1]:

А / Все S суть Р/ -* Е / Ни одно S не есть не -Р/. При­мер: «Все дороги ведут в Рим» -> «Ни одна дорога не ведет мимо Рима».

Е /Ни одно S не есть Р/-* A /Bсe S суть не -Р/. Пример: «Ни один студент нашей группы не является неуспеваю­щим» -* «Все студенты нашей группы являются успеваю­щими».

I /Некоторые S суть P/-* L /Некоторые S не суть не -Р/. Пример: «Некоторые бизнесмены есть миллионеры» -* «Не­которые бизнесмены не являются немиллионерами».

О /Некоторые S не суть Р/ —> I /Некоторые S суть не - Р/. Пример: «Некоторые члены акционерного общества не являются его учредителями» -*- «Некоторые члены акци­онерного общества являются не учредителями».

Обращением   суждения  называется  такая   логическая операция, при которой из данного суждения образуется но­вое, в котором субъектом становится предикат исходного суждения, а предикатом — субъект исходного суждения. Проще говоря, при обращении происходит перемена мест субъекта и предиката при сохранении качества суждения. Например, суждение «Только квадраты являются равносто­ронними прямоугольниками» можно обратить в суждение «Все равносторонние прямоугольники являются квадрата­ми». В приведенном примере мы наблюдаем простое, чис­тое обращение, т. е. перемену мест субъекта и предиката без изменения их объема.

2. Виды непосредственных умозаключений

Превращение - разновидность непосредственного умозаключения, при котором изменяется качество посылки без изменения ее количества. Оно осуществляется двумя способами[2]:

а) Путем двойного отрицания, которое ставится перед связкой и перед предикатом: S есть Р -> S не есть не-Р. Например: "Все студенты - учащиеся"; "Ни один студент не является не учащимся". Двойное отрицание равносильно утверждению.

б) Путем перевода отрицания из предиката в связку: S есть не-Р -> S не есть Р. Например: "Некоторые философы признают возможность недиалектического мышления" -> "Некоторые философы не признают возможность диалектического мышления".

Превращению подлежат все четыре вида суждений по объединенной классификации: А- > Е , Е -> А , I->0 , О- >I.

Как видим, для превращения суждения необходимо заменить его связку на противоположную, а предикат - на понятие, противоречащее предикату исходного суждения. Смысл превращения заключается в следующем: заключение, полученное посредством превращения, уточняет наше знание. Устанавливая отношения между субъектом и понятием, противоречащим предикату исходного суждения, мы рассматриваем предмет суждения с новой стороны, фиксируя внимание на свойстве, не совместимом со свойством, отраженном в предикате исходного суждения. Это знание выражает тот факт, что предмет не может иметь и вместе с тем не иметь одно и то же свойство. Поэтому заключение, полученное с помощью этой логической операции, содержит некоторое новое знание о предмете.

Обращение - непосредственное умозаключение, в котором происходит перемена мест субъекта и предиката при сохранении качества связки.

Обращение подчиняется правилу распределенности терминов, согласно которому субъект распределен в общих и не распределен в частных суждениях, предикат распределен в отрицательных и не распределен в утвердительных суждениях. В соответствии с этим правилом суждения, различные по количеству и качеству, обращаются следующим образом:[3]

Все S есть Р -> Некоторые Р есть S. Например: "Все студенты первого курса сдали зачет по логике" -> "Некоторые сдавшие зачет по логике - студенты первого курса".  

Ни одно S не есть Р -> Ни одно Р не есть S. Например: "Ни один студент второй учебной группы не является неуспевающим" -> "Ни один неуспевающий не является студентом второй учебной группы".

Некоторые S есть Р -> Некоторые Р есть S. Например: "Некоторые студенты - участники спартакиады" -> "Некоторые участники спартакиады - студенты

Необходимо отметить, что частноотрицательные суждения не обращаются.

Смысл обращения заключается в следующем: используя этот логический прием, мы уточняем наши знания, придаем им большую определенность, так как предметом нашей мысли становится предмет, отраженный предикатом исходного суждения. Однако при этом необходимо строго соблюдать правила ограничения. Если их нарушить, то это приведет к ошибкам в рассуждении.

Противопоставление предикату - непосредственное умозаключение, которое предполагает получение заключения, где субъектом является понятие, противоречащее предикату исходного суждения, а предикатом является субъект исходного суждения. Нетрудно заметить, что данный вид умозаключения можно рассматривать как результат одновременного превращения и обращения: превращая исходное суждение " S есть Р ", устанавливается отношение S к не-Р,  суждение, полученное путем превращения, обращается; в результате устанавливается отношение не-Р к S[4] .

Заключение, полученное путем противопоставления предикату, зависит от количества и качества исходного суждения. В соответствии с этим данный вид непосредственного умозаключения осуществляется следующим образом.

Все S есть Р -> Ни одно не-Р не есть S. Например: "Все офицеры - военнослужащие" -> "Ни один не военнослужащий не является офицером".

Ни одно S не есть Р -> Некоторые не-Р есть S. Например: "Ни одна захватническая война не является справедливой" -> "Некоторые несправедливые войны являются захватническими".

Частноутвердительные суждения посредством противопоставления предикату не преобразуются.

Некоторые S не есть Р -> Некоторые не-Р есть S. Например: "Некоторые актеры не являются пианистами" -> "Некоторые не пианисты - актеры".

Смысл умозаключений посредством противопоставления предикату состоит в том, что в них выясняется отношение предметов, не входящих в объем предиката, к предметам, отраженным субъектом исходного суждения. Устанавливая отношения между этими предметами, мы уточняем наши знания, высказываем нечто новое, что не было в явной форме выражено в исходном суждении.

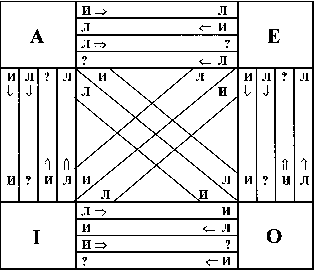Умозаключение по логическому квадрату это такой вид непосредственных умозаключений, который позволяет получать выводы, учитывая правила соотношений истинности - ложности между категорическими суждениями А, Е, I, О[5]. Отношения между данными суждениями, как уже указывалось, иллюстрированы схемой логического квадрата. При этом устанавливается следование истинности или ложности одного суждения из истинности или ложности другого суждения в соответствии с темилогическими законами, которые проявляют себя в соответствующих отношениях. Используя схему логического квадрата, в общем виде это можно представить таким образом.

Например, пусть дано истинное суждение A: "Все войны есть продолжение политики насильственными средствами". Из него следуют выводы:

Е - "Ни одна война не является продолжением политики насильственными средствами" - ложное;

I - "Некоторые войны являются продолжением политики насильственными средствами" - истинное;

О - "Некоторые войны не являются продолжением политики насильственными средствами" - ложное.

Приведенная схема логического квадрата позволяет правильно осуществить данный вид непосредственного умозаключения. Смысл умозаключений по логическому квадрату состоит в том, что знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения. Эти выводы основаны на определенных правилах, нарушение которых приводит к ошибкам, выражающимся в том, что ложные суждения принимаются за истинные, а истинные - за ложные.