ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
ОТЧЕТ ПО ВЫПОЛНЕНИЮ
ЛАБОРАТОРНЫХ РАБОТ
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И
ПРИКЛАДНЫЕ МОДЕЛИ
ВАРИАНТ 2
Калуга 2008 г
Задача 1
Условие
задачи:
На
фабрике шьют два вида костюмов. Для пошива которых используется два вида
тканей. Количество тканей ограничено. Известны затраты ресурсов на производство этих
костюмов, предельные нормы ресурсов, выручка за единицу продукции. Необходимо
оптимизировать выручку фабрики.
|
Виды костюмов
|
Нормы расхода сырья
на единицу продукции
|
Запасы
сырья
|
|
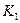
|
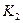
|
|
|
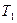
|
4
|
6
|
900
|
|
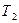
|
5
|
7
|
1000
|
|
Цена изделия
|
14
|
12
|
|
Составим экономико–математическую модель задачи
оптимального использования ресурсов на максимум прибыли. В качестве неизвестных
примем объем выпуска продукции j- го вида 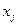 ( j = 1, 2, 3 )
( j = 1, 2, 3 )
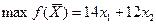
Функциональные ограничения:
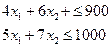
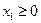 ,
, 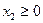 .
.
Оптимальный план выпуска найдем с помощью надстройки
Excel Поиск решения.
Рассмотрим технологию решения задачи в среде Excel.
1.
Укажем адреса ячеек, в которые будет помещен результат
решения (изменяемые ячейки).
Обозначим через 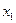 ,
, 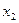 , количество костюмов каждого вида. В данной задаче
оптимальное значение вектора
, количество костюмов каждого вида. В данной задаче
оптимальное значение вектора 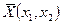 будут помещены в
ячейки B2:C2, оптимальное
значение целевой функции – в ячейке E2.
будут помещены в
ячейки B2:C2, оптимальное
значение целевой функции – в ячейке E2.
2.
Введем исходные данные (рисунок 1)
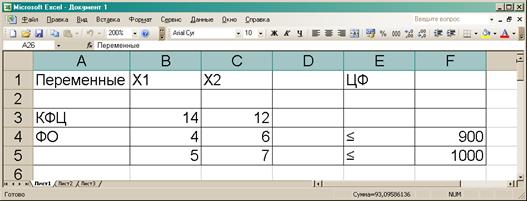
Рис. 1
Исходные данные
3.
Введем зависимость для целевой функции
1. Выделить ячейку Е2.
2. Вызвать мастер функций, расположенный на панели
инструментов.
3. В окне Категория
выбрать категорию Математические.
4. В окне Функции
выбрать строку СУММПРОИЗВ.
5. В строку Массив1 ввести B2:С2.
6. В строку массив2 ввести B3:C3.
4. Заполним ячейки D4:D5
1. Выделить ячейку D4
2. Вызвать мастер функций, расположенный на панели
инструментов
3. В окне категория выбрать категорию Математические
4. В окне функции выбрать строку СУММПРОИЗВ
5. В строку Массив1 ввести B2:C2
6. В строку массив2 ввести B4:C4
Аналогичную
операцию произведем с ячейкой D5
7.
Запустить команду Поиск решения
8. Назначить
ячейку для целевой функции
(установить целевую ячейку), указать адреса изменяемых ячеек, ввести
ограничения (Рисунок 2).
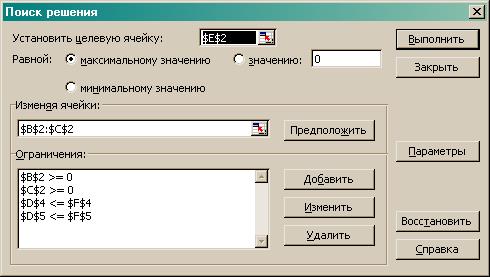
Рис 2. Введены
все условия задачи
9. Ввести параметры для решения задачи линейного
программирования
В диалоговом окне поместить указатель мыши на кнопку
параметры. На экране появится диалоговое окно Параметры Поиск решения.
Установить флажки, как показано на рисунке 3.
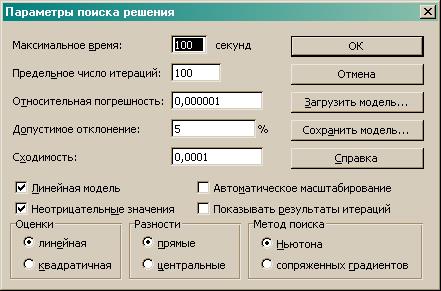
Рис 3. Ввод параметров
Поместить указатель мыши на кнопку Выполнить. В
результате Поиска решения появляется исходная таблица с заполненными ячейками D4:D5 для значений 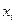 и ячейка E2 с максимальным значением целевой функции (рисунок 4).
и ячейка E2 с максимальным значением целевой функции (рисунок 4).
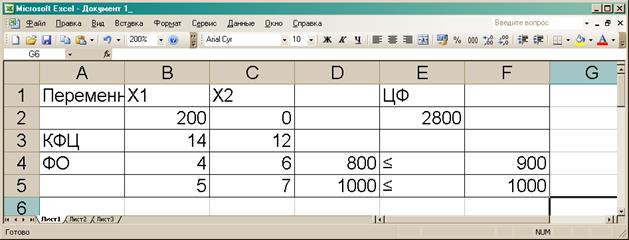
Рис. 4 Полученное реение
Полученное решение означает, что максимальный доход 2800
тыс.руб. предприятие может получить при выпуске 200 костюмов первого вида и 0
костюмов второго вида. При этом второй
тип сырья будет использован полностью.
EXCEL позволяет представить результаты поиска решения в
форме отчета.
Рассмотрим отчет по результатам.
В данный отчет включаются исходные и конечные значения
целевой ячейки, изменяемых ячеек, а также приводятся дополнительные сведенья об
ограничениях.
В отчете по результатам содержится оптимальное
значение переменных X1
и X2 , которые соответственно равны
233,33 и 33,33, значение целевой функции 1366,67.
Рассмотрим отчет по устойчивости.
Данный отчет содержит сведенья о чувствительности
решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
В
отчете по устойчивости можно найти решение двойственной задачи. Теневые цены
(двойственные оценки) ресурсов X1 и X2 соответственно равны -7,543796423 и 0,978803475.
Т.к. эти ресурсы имеют отличные от нуля оценки, то полностью используются в
оптимальном плане и являются дефицитными, сдерживающими рост целевой функции.
В отчете по устойчивости можно также получить
информацию о влиянии изменения правых частей ограничений на значение целевой
функции (чувствительность решения к изменению запасов сырья).
Известно, что оценки не меняют своей величины, если не
меняется набор векторов, входящих в базис оптимального плана, тогда как
интенсивности этих векторов (значения неизвестных) в плане могут меняться. Поэтому
необходимо знать такие интервалы изменения каждого из свободных членов системы
ограничений ЗЛП, или интервалы устойчивости двойственных оценок, в которых
оптимальный план двойственной задачи не менялся бы. Эту информацию можно
получить из Отчета по устойчивости, рисунок 5.
|
Ограничение
|
Допустимое
|
Допустимое
|
|
Правая
часть
|
Увеличение
|
Уменьшение
|
|
1
|
1,125
|
0,227272727
|
|
17
|
5
|
9
|
Рис 5 Фрагмент отчета
по устойчивости
В данной задаче видно, что запасы дефицитных ресурсов X1 и X2 могут быть,
как уменьшены, так и увеличены.
В первой части отчета по устойчивости содержится
информация о допустимом увеличении и уменьшении коэффициентов целевой функции,
при которых не меняется оптимальный план исходной задачи рисунок 6.
|
Целевой
|
Допустимое
|
Допустимое
|
|
Коэффициент
|
Увеличение
|
Уменьшение
|
|
13,98988002
|
1E+30
|
13,70324865
|
|
0,286631375
|
13,70324865
|
1E+30
|
Рис 6 Фрагмент отчета
об устойчивости
Задача 2
Задача
нелинейной оптимизации
Формирование портфеля минимального риска при заданной
доходности
Условие
задачи:
Пусть перед инвестором стоит задача сформировать
инвестиционный портфель из двух видов ценных бумаг. Портфель может иметь
минимальный риск, но отвечать требованиям заданной доходности. Необходимо
минимизировать риск портфеля в целом при условии, что существует требование
определенной доходности портфеля.
Пусть X1 – удельный вес бумаг типа А в
инвестиционном портфеле;
X2 - удельный
вес бумаг типа В в инвестиционном портфеле;
M1 –
доходность бумаг А;
M2 –
доходность бумаг Б;
Мр
– доходность портфеля в целом;
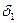 - риск бумаг А
- риск бумаг А
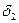 - риск бумаг В
- риск бумаг В
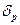 - риск портфеля в
целом
- риск портфеля в
целом
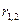 - коэффициент
корреляции между доходностями бумаг А и B.
- коэффициент
корреляции между доходностями бумаг А и B.
|
А
|
В
|
Обязательная доходность
|
|
Мi
|
22
|
8
|
17
|
|
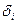
|
14
|
1
|
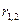 = 0,25
= 0,25
Математическая модель задачи:
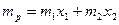
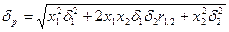
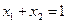
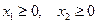
1.
Укажем адреса ячеек, в которые будет помещен результат
решения (изменяемые ячейки).
Обозначим через 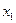 ,
, 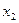 , количество костюмов каждого вида. В данной задаче
оптимальное значение вектора
, количество костюмов каждого вида. В данной задаче
оптимальное значение вектора 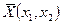 будут помещены в
ячейки B2:C2, оптимальное
значение целевой функции – в ячейке E2.
будут помещены в
ячейки B2:C2, оптимальное
значение целевой функции – в ячейке E2.
2.
Введем исходные данные (рисунок 1)
Решение
задачи получим в табличном редакторе EXCEL с помощью надстройки Поиск решения.
Исходные
данные введем, как показано на рисунке 1

Рис 1. Исходные
данные
Запустим команду Поиск решения
3.
Введем формулу риска портфеля
1.
Выделить ячейку
Е2.
2.
Вызвать мастер
функций, расположенный на панели инструментов.
3.
В окне Категория выбрать категорию Математические.
4.
В окне Функции выбрать строку КОРЕНЬ.
5.
В строку Число введем формулу
=КОРЕНЬ(B2*B2*B3*B3+2*B2*C2*B3*C3*0,25+C2*C2*C3*C3)
4.
Заполним ячейки D4:D5
7.
Выделить ячейку D4
8.
Вызвать мастер
функций, расположенный на панели инструментов
9.
В окне категория
выбрать категорию Математические
10.
В окне функции
выбрать строку СУММПРОИЗВ
11.
В строку Массив1
ввести B2:C2
12.
В строку массив2
ввести B4:C4
Аналогичную
операцию произведем с ячейкой D5
10.
Запустить команду Поиск решения
11.
Назначить ячейку для целевой функции (установить целевую ячейку), указать адреса
изменяемых ячеек, ввести ограничения (Рисунок 2).
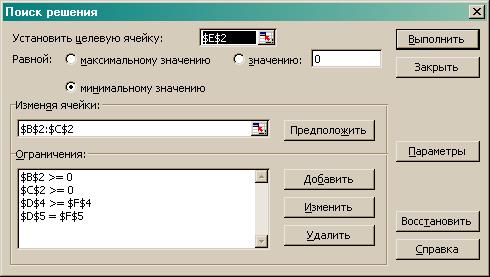
Рис 2. Введены все
условия задачи
12.
Ввести параметры для решения задачи линейного
программирования
В диалоговом окне поместить указатель мыши на кнопку
параметры. На экране появится диалоговое окно Параметры Поиск решения.
Установить флажки, как показано на рисунке 3.
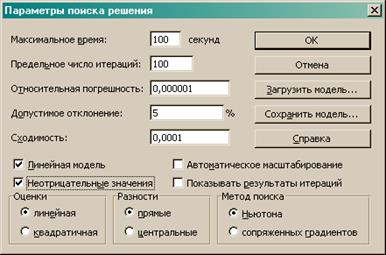
Рис.
3. Параметры Поиска решения
Результаты решения приведены
на рисунке 4.
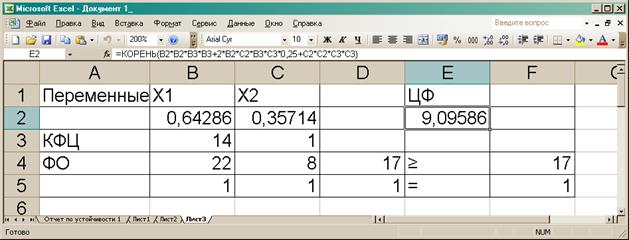
Рис.
4. Решение получено
Результаты решения означают, что минимальный риск
портфеля ценных бумаг равен 9,09586 % и достигается при X1 = 0,64286 и X2 =
0,35714.
Задача 3
Условие
задачи:
Даны
коэффициенты прямых поставок aij и конечный продукт yi для трехотраслевой экономической системы:
 0 0,1
0,1 180
0 0,1
0,1 180
А= 0,1
0,2 0,1 , Y= 200
0,2
0,1 0,2 200
Требуется
определить:
1) межотраслевые поставки;
2) Проверить продуктивность
матрицы А.
1.
Элементы матрицы прямых материальных затрат запишем в ячейки В2:D4.
2. В ячейки В6:D8 запишем элементы матрицы Е-А. Массив
Е-А задан как диапазон ячеек. Выделим диапазон В10:D12 для размещения обратной
матрицы В=(Е-А)-1 и введем формулу для вычисления МОБР(В6:D8). Затем
следует нажать клавишу F2, затем нажать
клавиши CTRL+SHIFT+ENTER. Все элементы матрицы полных затрат В не отрицательны,
следовательно, матрица А продуктивна.
3. В ячейки G10:G12 запишем элементы вектора конечного
продукта Y. Выделим диапазон ячеек В15:В17 для размещения вектора валового
выпуска X, вычисляемого по формуле X=(Е-А)-1*Y. Затем введем формулу
для вычисления МУМНОЖ(В10:D12, G10:G12). Затем следует нажать клавишу F2, затем комбинацию клавиш CTRL+SHIFT+ENTER.
4. Межотраслевые поставки 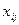 вычисляются по формуле
вычисляются по формуле
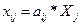
Выделим диапазон ячеек В20:В22 для размещения
межотраслевых поставок и введем формулу для вычислений МУМНОЖ(В2:В4;В15). Затем
следует нажать клавишу F2, затем
комбинацию клавиш CTRL+SHIFT+ENTER.
Аналогично заполним ячейки С20:С22 и D20:D22.
Все результаты представлены на рисунке 1.
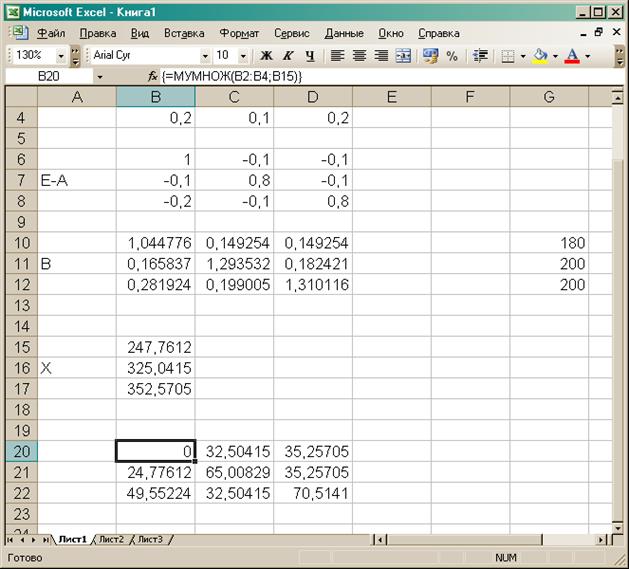
Рис.
1. Резутаты решения задачи
5. Заполним схему МОБ (Рисунок 2).
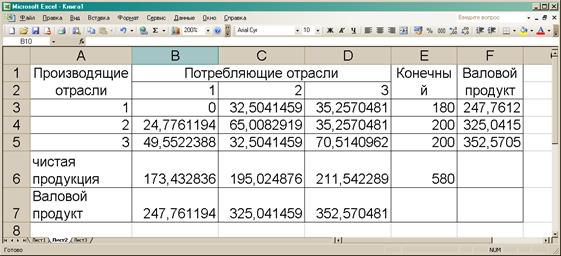
Рис.
2. Схема МОБ
Задача 4
Условие задачи:
Исходные данные транспортной задачи
приведены схематически: внутри прямоугольника заданы удельные транспортные
затраты на перевозку единицы груза, слева указаны мощности поставщиков, а
сверху – мощности потребителей. Сформулировать модель исходной транспортной
задачи, найти оптимальный план закрепления поставщиков за потребителями,
установить единственность оптимального плана, используя Поиск решения.
|
Мощности
поставщиков
|
Мощности
потребителей
|
|
150
|
350
|
200
|
100
|
100
|
|
500
|
3
|
3
|
5
|
3
|
1
|
|
300
|
4
|
3
|
2
|
4
|
5
|
|
100
|
3
|
7
|
5
|
4
|
1
|
1. Создадим
форму для решения задачи, т.е. создадим матрицу назначения по должностям.
Для этого выполним резервирование изменяемых ячеек: в
блок ячеек В3:F5 введем «1».
Т.о. резервируется место, где после решения задачи
будет находиться распределение рабочих по должностям, обеспечивающее
максимальную производительность труда.
2. Введем
граничные условия, т.е. введем условия реализации мощностей всех поставщиков.
1.
Выделим ячейку A3.
2.
Щелкаем знак «  ».
».
3.
Выделяем
необходимые для суммирования ячейки B3:F3.
4.
Нажимаем ENTER.
5.
С помощью Автозаполнения заполним ячейки А4:А5.
3. Введем
условия заполнения вакантной должности.
1.
Выделим ячейку В2.
2.
Щелкаем по знаку
«  », при этом автоматически выделяется весь столбец В3:В5.
», при этом автоматически выделяется весь столбец В3:В5.
3.
Нажимаем ENTER.
4.
С помощью Автозаполнения заполним ячейки С6:F6.
Т.о., введены ограничения по назначению работника
только на одну должность и условию заполнения всех вакантных мест.
Форма
для ввода условий задачи представлена на рисунке 1.
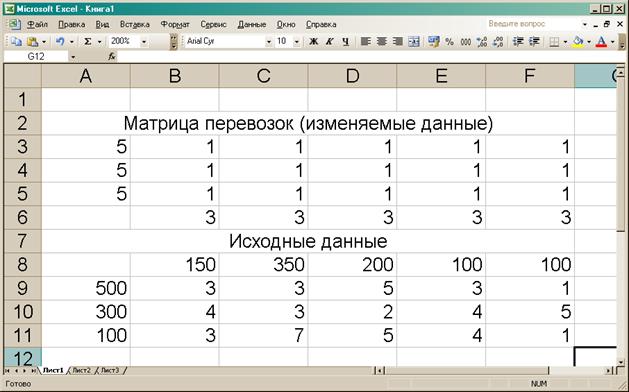
Рис. 1 Создание формы
для ввода условий задачи
4. Назначим целевую функцию.
1.
Выделим ячейку
целевой функции В13.
2.
Вызываем Мастер
функций.
3.
В окне категория
выбираем Математические.
4.
В окне функция выбраем СУММПРОИЗВ.
5.
Нажимаем ОК.
6. В окне СУММПРОИЗВ указать адреса массивов, элементы
которых обрабатываются этой функцией:
В поле массив 1 указать адреса ячеек В3: F5;
В поле массив 2 – В10:Е13.
7. Нажимаем ОК.
В поле ячейки B13 появится числовое значение, равное произведения «1»
на производительность каждого работника на конкретной должности.
5.Введем
зависимости из математической модели
1.
Щелкнуть Сервис -
Поиск решений.
2. В поле установить целевую ячейку ввести адрес В13.
3. Установить направление изменения целевой функции,
равное «максимальному значению».
4. Ввести адреса изменяемых ячеек В3:F5.
5. Ввести ограничения задачи, как показано на рисунке 2.
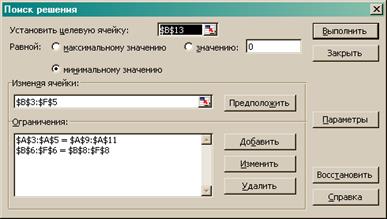
Рис.
2. Диалоговое окно Поиск решений
6. Далее установить ограничения на решение задачи. Для
этого следует щелкнуть параметры и установить флажки как показано на рисунке 3.
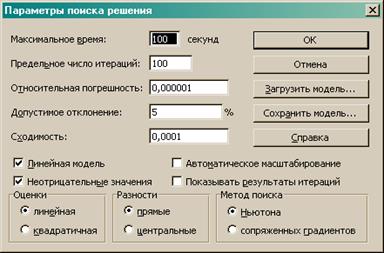
Рис.
3. Ввод параметров поиска решений
7. Нажимаем Выполнить.
В результате решения получен
оптимальный план перевозок (Рисунок 4).
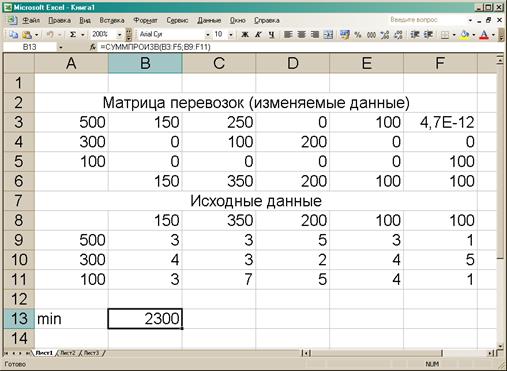
Рис. 4. Оптимальный
план перевозок
Х1,2
= 250 ед. груза следует перевезти от 1-ого поставщика 3-ему потребителю.
Х2,3
= 200 ед. груза перевезти от 2-ого поставщика 3-ему потребителю.
Х3,1
= 0 ед. груза перевезти от 3-ого поставщика 1-ему потребителю.
Общая
стоимость перевозок равна 2300.
Используемая
литература
1.
Экономико–
математические методы и прикладные модели, Под ред. Учеб. Пособие для вузов/ В.В. Федосеев, А.Н.
Гармаш, Д.М. Дайитбегов и др.; Под редакцией В.В. Федосеева. – М.: ЮНИТИ, 1999.
– 391 с.
2.
Экономико–математическое
моделирование / Под ред. проф. И.В.Орловой: Практическое пособие по решению
задач. – М.: Вузовский учебник, 2004. – 144 с.
3.
Экономико
– математические методы и модели. Выполнение расчетов в среде EXCEL/ Под ред.
проф. И.В.Орловой / Практикум: Учебное пособие для вузов. – М.: ЗАО
«Финстатинформ», 2000. – 136 с.