Задача
1.
1.1
Выяснить, существует ли связь между
потреблением дизельного топлива (y) и объёмом
валовой продукции (
). (Для этого построить поле рассеяния. На основе его
визуального анализа выдвинуть гипотезу о виде статистической зависимости y от ). Найти точечные оценки неизвестных параметров модели.
Выяснить, существует ли связь между потреблением дизельного топлива (y) и объёмом капитальных вложений (
). Найти оценки неизвестных параметров модели.
Решение.
|
Годы
|
Валовая продукция
промышленности
( млрд. р.)
|
Объём
капитальных вложений
( млрд. р.)
|
Объём потребления дизельного топлива
(y
млн. т.)
|
|
1985
|
3,4
|
1,8
|
0,9
|
|
1986
|
3,2
|
1,7
|
1,3
|
|
1987
|
2,9
|
1,6
|
1,4
|
|
1988
|
3,1
|
1,4
|
1,1
|
|
1989
|
3,3
|
1,6
|
0,8
|
|
1990
|
3,4
|
1,8
|
0,6
|
|
1991
|
3
|
1,4
|
0,6
|
|
1992
|
3,3
|
2
|
0,9
|
|
1993
|
4,3
|
2,4
|
1,1
|
|
1994
|
4,4
|
2,7
|
1,4
|
|
1995
|
4,7
|
2,5
|
1,9
|
|
1996
|
4,3
|
2,4
|
1,9
|
|
1997
|
4,5
|
2,3
|
1,3
|
|
1998
|
4,6
|
2,7
|
2,4
|
|
1999
|
4,6
|
2,5
|
2,2
|
|
2000
|
4,5
|
2,9
|
2
|
Используя
таблицу, строим поля рассеяния.
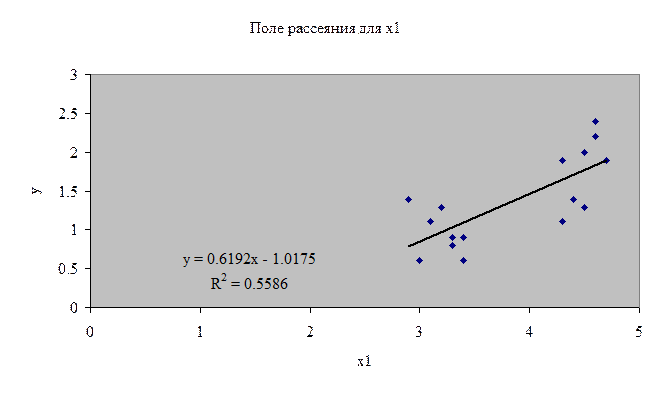
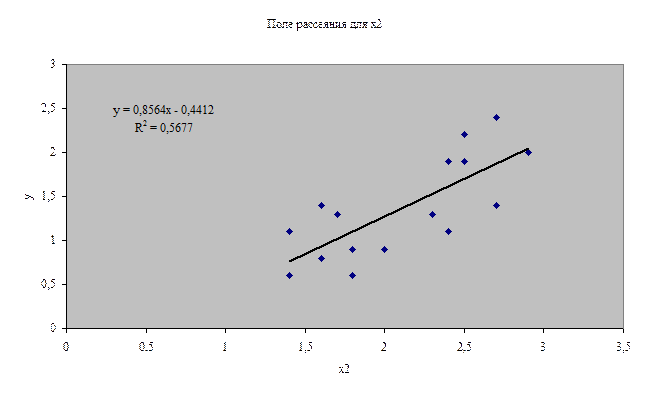
На
основе анализа поля рассеяния (см. рис. 1.) выдвигаем гипотезу о том, что
зависимость потребления дизельного топлива (y) от объёмов продукции () описывается линейной моделью вида:
где
и 
-неизвестные
постоянные коэффициенты, а u –
отклонение, вызванное влиянием неучтённых факторов и погрешностями измерений.
Аналогично,
между y и зависимость
описывается моделью:
Задача
состоит в получении уравнения регрессии:
неизвестные
коэффициенты находятся по формулам (используя метод наименьших квадратов
(МНК)):
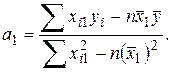
и
с помощью таблицы:
|
|
|
y
|
|
|
|
|
|
|
|
1
|
3,4
|
1,8
|
0,9
|
11,56
|
3,24
|
3,06
|
1,62
|
6,12
|
0,81
|
|
2
|
3,2
|
1,7
|
1,3
|
10,24
|
2,89
|
4,16
|
2,21
|
5,44
|
1,69
|
|
3
|
2,9
|
1,6
|
1,4
|
8,41
|
2,56
|
4,06
|
2,24
|
4,64
|
1,96
|
|
4
|
3,1
|
1,4
|
1,1
|
9,61
|
1,96
|
3,41
|
1,54
|
4,34
|
1,21
|
|
5
|
3,3
|
1,6
|
0,8
|
10,89
|
2,56
|
2,64
|
1,28
|
5,28
|
0,64
|
|
6
|
3,4
|
1,8
|
0,6
|
11,56
|
3,24
|
2,04
|
1,08
|
6,12
|
0,36
|
|
7
|
3
|
1,4
|
0,6
|
9
|
1,96
|
1,8
|
0,84
|
4,2
|
0,36
|
|
8
|
3,3
|
2
|
0,9
|
10,89
|
4
|
2,97
|
1,8
|
6,6
|
0,81
|
|
9
|
4,3
|
2,4
|
1,1
|
18,49
|
5,76
|
4,73
|
2,64
|
10,32
|
1,21
|
|
10
|
4,4
|
2,7
|
1,4
|
19,36
|
7,29
|
6,16
|
3,78
|
11,88
|
1,96
|
|
11
|
4,7
|
2,5
|
1,9
|
22,09
|
6,25
|
8,93
|
4,75
|
11,75
|
3,61
|
|
12
|
4,3
|
2,4
|
1,9
|
18,49
|
5,76
|
8,17
|
4,56
|
10,32
|
3,61
|
|
13
|
4,5
|
2,3
|
1,3
|
20,25
|
5,29
|
5,85
|
2,99
|
10,35
|
1,69
|
|
14
|
4,6
|
2,7
|
2,4
|
21,16
|
7,29
|
11,04
|
6,48
|
12,42
|
5,76
|
|
15
|
4,6
|
2,5
|
2,2
|
21,16
|
6,25
|
10,12
|
5,5
|
11,5
|
4,84
|
|
16
|
4,5
|
2,9
|
2
|
20,25
|
8,41
|
9
|
5,8
|
13,05
|
4
|
|
 сумма
|
61,5
|
33,7
|
21,8
|
243,41
|
74,71
|
88,14
|
49,11
|
134,33
|
34,52
|
|
средние
|
15,21313
|
4,669375
|
2,1575
|
|
|
|
n=16, 
Следовательно,
Таким
образом, 
Аналогично
находятся оценки коэффициентов модели
а именно, 
1.2.
По найденным в п. 1.1. уравнениям регрессии построить доверительные интервалы
потребления дизельного топлива, соответствующие вероятности 0,9 при следующих значениях независимой
переменной: 
Построить доверительную полосу для уравнения регрессии.
Изобразить на графике поля рассеяния, прямые регрессии и доверительные полосы.
Решение.
Доверительные
интервалы среднего потребления дизельного топлива для уравнения парной линейной
регрессии находятся по формуле
где
соответственно верхняя
и нижняя границы доверительного интервала; 
значение независимой переменной 
для которого
определяется доверительный интервал, 
квантиль распределения Стьюдента, 
доверительная вероятность, (n-2) – число степеней свободы;
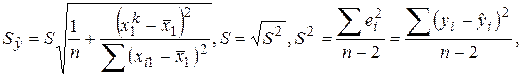
Рассмотрим
уравнение Пусть 
тогда 
.
Используя
вспомогательную таблицу:
|
i
|
|
|
|
|
1
|
1,0877
|
0,0971
|
-0,4602
|
|
2
|
0,9639
|
0,1130
|
-0,6438
|
|
3
|
0,7781
|
0,3867
|
-0,9438
|
|
4
|
0,9020
|
0,0392
|
-0,7438
|
|
5
|
1,0258
|
0,0510
|
-0,5438
|
|
6
|
1,0877
|
0,2379
|
-0,4438
|
|
7
|
0,8401
|
0,0576
|
-0,8438
|
|
8
|
1,0258
|
0,0158
|
-0,5438
|
|
9
|
1,6450
|
0,2970
|
0,4563
|
|
10
|
1,7069
|
0,0942
|
0,5563
|
|
11
|
1,8927
|
0,0001
|
0,8563
|
|
12
|
1,6450
|
0,0650
|
0,4563
|
|
13
|
1,7688
|
0,2198
|
0,6563
|
|
14
|
1,8308
|
0,3240
|
0,7563
|
|
15
|
1,8308
|
0,1363
|
0,7563
|
|
16
|
1,7688
|
0,0534
|
0,6563
|
|
сумма
|
|
2,1882
|
|
|
сумма квадратов
|
7,0352
|
Получим
и заполним таблицу:
|
|
|
|
|
|
|
|
2,900
|
0,778
|
0,172
|
0,475
|
1,081
|
|
|
3,844
|
1,363
|
0,099
|
1,188
|
1,537
|
|
|
4,700
|
1,893
|
0,161
|
1,608
|
2,177
|
График
уравнения регрессии, и доверительные интервалы и доверительная полоса приведены
на рис.
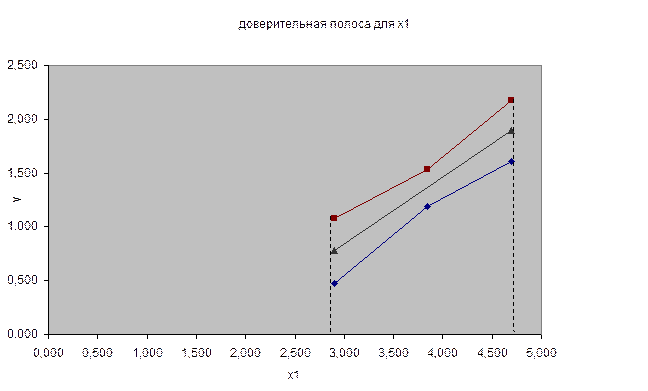
Аналогично
находятся доверительные интервалы для уравнения Используем
вспомогательную таблицу:
|
I
|
|
|
|
|
1
|
1,1002
|
0,0401
|
-0,3063
|
|
2
|
1,0146
|
0,0815
|
-0,4063
|
|
3
|
0,9290
|
0,2219
|
-0,5063
|
|
4
|
0,7577
|
0,1172
|
-0,7063
|
|
5
|
0,9290
|
0,0166
|
-0,5063
|
|
6
|
1,1002
|
0,2502
|
-0,3063
|
|
7
|
0,7577
|
0,0249
|
-0,7063
|
|
8
|
1,2715
|
0,1380
|
-0,1063
|
|
9
|
1,6141
|
0,2643
|
0,2938
|
|
10
|
1,8710
|
0,2218
|
0,5938
|
|
11
|
1,6997
|
0,0401
|
0,3938
|
|
12
|
1,6141
|
0,0818
|
0,2938
|
|
13
|
1,5284
|
0,0522
|
0,1938
|
|
14
|
1,8710
|
0,2799
|
0,5938
|
|
15
|
1,6997
|
0,2503
|
0,3938
|
|
16
|
2,0422
|
0,0018
|
0,7938
|
|
сумма
|
|
2,0824
|
|
|
cумма
квадратов
|
3,729
|
|
Получим
и заполним таблицу:
|
|
|
|
|
|
|
|
0,1709
|
0,4568
|
1,0586
|
0,1709
|
0,4568
|
|
|
0,0964
|
1,1927
|
1,5323
|
0,0964
|
1,1927
|
|
|
0,1855
|
1,7155
|
2,369
|
0,1855
|
1,7155
|
График
уравнения регрессии, и доверительные интервалы и доверительная полоса приведены
на рис.
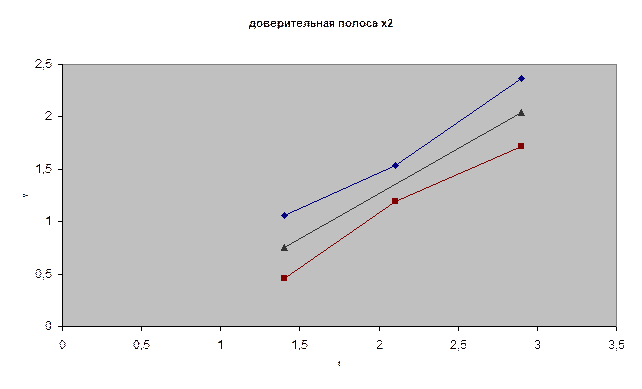Задача 2.
2.1.
Найти все коэффициенты парной корреляции, проверить их значимость и
проанализировать тесноту линейной связи между всеми парами переменных.
Решение.
Коэффициент
парной корреляции находится по формуле:
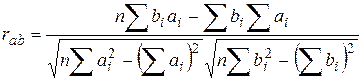
Подставляя
соответствующие значения, получим 
0,7474. Так как
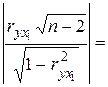3,8 >1,761
, то 
существенно отличается
от 0 и существует сильная линейная положительная связь между y и .
Аналогично
проверим неравенство для 
0,7535:
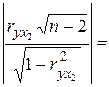8,01>1,761, значит, 
также существенно отличается от 0 и существует сильная
линейная положительная связь между y и. .
Для 
0,9373:
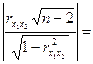4,95>1,761, значит, 
существенно отличается
от 0 и существует сильная линейная положительная связь между и .
2.2.
Найти по методу наименьших квадратов оценки коэффициентов линейной
регрессионной модели
Решение.
Уравнение
регрессии ищем в виде:
Обозначения
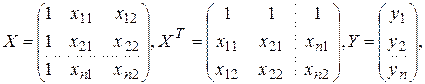
тогда
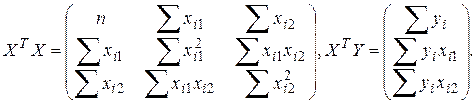
Вектор
находится по формуле: 
В
нашем случае
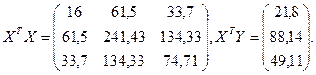
Тогда
.
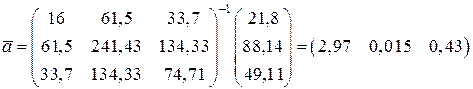Таким
образом, 
2.3.
Найти коэффициенты множественной корреляции и детерминации.
Решение.
Коэффициент
R множественной корреляции
определяется по формуле:
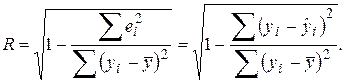
Воспользуемся
вспомогательной таблицей:
i
|
|
|
|
1
|
0,0306
|
-0,4625
|
|
2
|
0,2401
|
-0,0625
|
|
3
|
0,2550
|
0,0375
|
|
 4
|
0,0144
|
-0,2625
|
|
5
|
0,0702
|
-0,5625
|
|
6
|
0,3025
|
-0,7625
|
|
7
|
0,4032
|
-0,7625
|
|
8
|
0,1764
|
-0,4625
|
|
9
|
0,0930
|
-0,2625
|
|
10
|
0,0081
|
0,0375
|
|
11
|
0,1056
|
0,5375
|
|
12
|
0,0576
|
0,5375
|
|
13
|
0,1980
|
-0,0625
|
|
14
|
0,3249
|
1,0375
|
|
15
|
0,0812
|
0,8375
|
|
16
|
0,0000
|
0,6375
|
|
Сумма квадратов
|
2,3610
|
4,8175
|
Тогда
R=0,9242.
Коэффициент
множественной детерминации 
равен квадрату
коэффициента множественной корреляции, то есть
=0,8541.
2.4.
В 2005г. планируется увеличение объёма валовой продукции на 1 млрд. р. по
сравнению с 2000г., а объём капитальных вложений – на 0,3 млрд. р. Дать
точечный и интервальный прогноз среднего потребления дизельного топлива в
2005г. при уровне доверия 0,9. (Считая, что объёмы валовой продукции и капитальных
вложений в 2005г. будут равны запланированным).
Решение.
Для
=5,5; 
= 3,2 получаем точечный прогноз: 
= 4,4273.
Для
нахождения интервального прогноза вычислим значения всех параметров, входящих в
формулу: 
, где , - соответственно
верхняя и нижняя границы доверительного интервала, 
- вектор независимых переменных, для которого определяется
интервал, 
=1,78 - квантиль распределения Стьюдента, 
- доверительная вероятность, n – количество наблюдений, (n-3)- число степеней свободы,
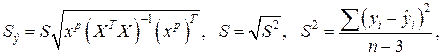
=0,415; 
=2,0319/13=0,1563; S =0,3953; 
=0,182;
И тогда = 4,879; = 3,9773.
2.5.
На основе полученных в задачах 1, 2 статистических характеристик провести содержательный экономический анализ
зависимости потребления дизельного топлива от объёмов валовой продукции сельского хозяйства и капитальных вложений.
Решение.
На
основании проведённых расчётов и полученных статистических характеристик можно
сделать определённые выводы относительно взаимосвязей между исследуемыми
экономическими показателями.
Так
как 0,7474 и проверка значимости показала его существенное
отличие от 0, то есть основания утверждать, что между y и существует достаточно
тесная положительная линейная зависимость, которая может быть отражена с
помощью найденного уравнения регрессии 
. Коэффициент 
= –1,0175 в данном
случае не имеет экономического смысла.
Коэффициент 
=0,6192 характеризует размер прироста потребления дизельного
топлива, обусловленного приростом объёма валового выпуска продукции сельского
хозяйства на единицу.
Значение 0,7535 свидетельствует о тесной линейной связи между y и :
Коэффициент 0,8564 в уравнении показывает, какого прироста
потребления дизельного топлива следует ожидать при увеличении объема
капитальных вложений на единицу.
Коэффициент
= -0,022 в уравнении показывает, что при
росте валового выпуска продукции промышленности на 1 млрд. р. и неизменном
объёме капитальных вложений следует
ожидать уменьшения потребления
дизельного топлива на 0,022 млн. тонн. Коэффициент 
= 1,025 показывает,
что при увеличении объёма капитальных вложений на 1 млрд. р. и неизменном объеме валовой продукции
промышленности следует ожидать увеличения потребления дизельного топлива на
1,025 млн. тонн.
Задача
3.
3.1.
Построить ломанную кривую изменения потребления дизельного топлива во времени.
Выдвинуть гипотезу о виде зависимости объёма потребления дизельного топлива от
времени. Записать трендовую модель, отражающую изменение потребления дизельного
топлива во времени. Оценить неизвестные параметры модели методом наименьших
квадратов.
Решение.
На
основании визуального наблюдения ломанной кривой, отражающей характер изменения
по годам объема потребления дизельного топлива, выдвигаем гипотезу о линейном
тренде. Следовательно, трендовая модель, отражающая изменение потребления
дизельного топлива, запишется в виде
где
- неизвестные параметры, u-случайное отклонение.
Коэффициенты
регрессионного уравнения тренда 
находятся по методу
наименьших квадратов и равны:
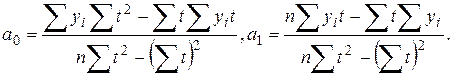
Воспользуемся
вспомогательной таблицей:
|
t
|
y
|
ty
|
|
|
|
1
|
1
|
2,7
|
2,7
|
2,451
|
0,249
|
|
2
|
2
|
2,4
|
4,8
|
2,575
|
-0,175
|
|
3
|
3
|
2,4
|
7,2
|
2,699
|
-0,299
|
|
4
|
4
|
2,6
|
10,4
|
2,823
|
-0,223
|
|
5
|
5
|
2,9
|
14,5
|
2,947
|
-0,047
|
|
6
|
6
|
3,1
|
18,6
|
3,071
|
0,029
|
|
7
|
7
|
3,5
|
24,5
|
3,195
|
0,305
|
|
8
|
8
|
3,3
|
26,4
|
3,319
|
-0,019
|
|
9
|
9
|
3,7
|
33,3
|
3,443
|
0,257
|
|
10
|
10
|
4
|
40
|
3,567
|
0,433
|
|
11
|
11
|
3,8
|
41,8
|
3,691
|
0,109
|
|
12
|
12
|
3,1
|
37,2
|
3,815
|
-0,715
|
|
13
|
13
|
4
|
52
|
3,939
|
0,061
|
|
14
|
14
|
4,4
|
61,6
|
4,063
|
0,337
|
|
15
|
15
|
4,2
|
63
|
4,187
|
0,013
|
|
16
|
16
|
4
|
64
|
4,311
|
-0,311
|
|
cумма
|
136
|
54,1
|
502
|
54,100
|
|
|
сумма квадратов
|
1496
|
|
|
|
1,3190
|
И
получим =2,328; 
= 0,124. Следовательно, уравнение регрессии будет иметь вид 
3.2.
Для найденного уравнения регрессии построить доверительную полосу при уровне
доверия 0,9. Нарисовать её на графике вместе с линией регрессии.
Решение.
Доверительный
интервал для линейного тренда находится по формуле: 
где
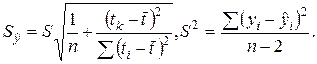
В
нашем случае:
= 8,5; = 0,094; S = 0,307.
Результат запишем в виде таблицы:
|
год
|
t
|
|
|
|
|
|
1985
|
1
|
2,4515
|
0,1128
|
2,2528
|
2,6502
|
|
1992
|
8
|
3,3193
|
0,2135
|
2,9433
|
3,6952
|
|
2000
|
16
|
4,3110
|
0,3412
|
3,7103
|
4,9118
|
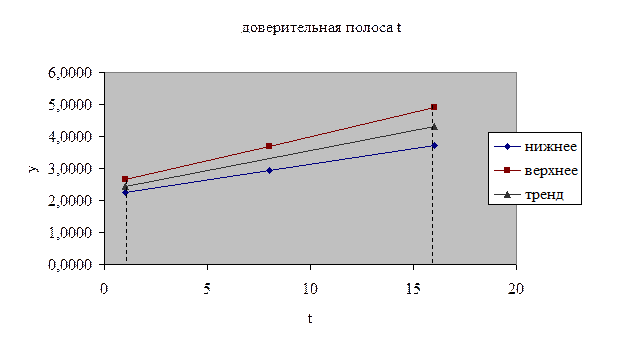
На рисунке. изображены график тренда, доверительные
интервалы (для t=1,8,16), и
доверительная полоса .
3.3. По линейному уравнению тренда найти точечный и
интервальный прогнозы среднего потребления дизельного топлива в 2005. и 2007г.
(доверительную вероятность принять равной 0,9). Изобразить на графике точечный
и интервальный прогноз.
Решение.
Тогда 
= 4,9309; 
= 5,1788. Аналогично пункту 3.2 решение запишем в виде
таблицы:
|
годы
|
t
|
|
|
|
|
|
2005
|
21
|
4,9309
|
0,4227
|
4,1866
|
5,6752
|
|
2007
|
23
|
5,1788
|
0,4554
|
4,3768
|
5,9809
|
На
рисунке изображены графики линейного тренда, точечные прогнозы 
, 
(обозначены точками на
прямой) и доверительные интервалы прогноза потребления дизельного топлива в
2005, 2007гг.
Задача
4.
4.2.
Для уравнений регрессии:
проверить
наличие или отсутствие автокорреляции, используя критерий Дарбина-Уотсона и
уровне значимости 
.
Решение.
Критерий
Дарбина-Уотсона имеет вид:
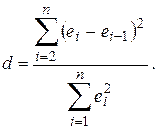
где
- отклонения от линии регрессии, i=1,..n.
Для
регрессионной модели 
:
Используя
таблицу:
|
|
|
|
1
|
-0,1782
|
|
|
2
|
-0,3143
|
-0,1362
|
|
3
|
-0,2205
|
0,09385
|
|
4
|
0,0864
|
0,30686
|
|
5
|
0,2882
|
0,20182
|
|
6
|
0,1849
|
-0,1032
|
|
7
|
0,3821
|
0,19713
|
|
8
|
-0,2193
|
-0,6014
|
|
9
|
-0,1182
|
0,10111
|
|
10
|
0,0836
|
0,20182
|
|
11
|
0,0951
|
0,01155
|
|
12
|
-0,5110
|
-0,6062
|
|
13
|
-0,1193
|
0,39173
|
|
14
|
0,4901
|
0,60938
|
|
15
|
0,2901
|
-0,2
|
|
16
|
-0,2196
|
-0,5097
|
|
сумм кв
|
1,1442
|
1,81658
|
Посчитаем
d=1,588.
У
нас n=16, m=2, , следовательно, условие 0,98=
>d>
=1,54 не выполняется, значит, автокорреляция
присутствует.
Для
используя таблицу:
|
|
|
|
I
|
0,249
|
|
|
2
|
-0,175
|
-0,42397
|
|
3
|
-0,299
|
-0,12397
|
|
4
|
-0,223
|
0,076029
|
|
5
|
-0,047
|
0,176029
|
|
6
|
0,029
|
0,076029
|
|
7
|
0,305
|
0,276029
|
|
8
|
-0,019
|
-0,32397
|
|
9
|
0,257
|
0,276029
|
|
10
|
0,433
|
0,176029
|
|
11
|
0,109
|
-0,32397
|
|
12
|
-0,715
|
-0,82397
|
|
13
|
0,061
|
0,776029
|
|
14
|
0,337
|
0,276029
|
|
15
|
0,013
|
-0,32397
|
|
16
|
-0,311
|
-0,32397
|
|
сумма
квадратов
|
1,3190
|
2,198207
|
Посчитаем
d=1,666. У нас n=16, m=1, , следовательно,
условие
1,1=<d<=1,37 не выполняется, значит, автокорреляция присутствует.
Для сначала найдём коэффициенты:
=8; 
=0,187.
Тогда уравнение регрессии имеет вид: 
|
|
|
|
1
|
4.7691
|
|
|
2
|
5.1557
|
0.3866
|
|
3
|
5.4423
|
0.2866
|
|
4
|
5.7289
|
0.2866
|
|
5
|
5.8155
|
0.0866
|
|
6
|
5.7021
|
-0.113
|
|
7
|
5.6887
|
-0.013
|
|
8
|
5.4753
|
-0.213
|
|
9
|
5.3619
|
-0.113
|
|
10
|
5.4485
|
0.0866
|
|
11
|
5.8351
|
0.3866
|
|
12
|
6.1217
|
0.2866
|
|
13
|
5.8083
|
-0.313
|
|
14
|
6.1949
|
0.3866
|
|
15
|
6.3815
|
0.1866
|
|
16
|
6.2681
|
-0.113
|
|
сумм
кв
|
522.524166
|
0.9271
|
Тогда
d=0,002. У нас n=16, m=1, , следовательно, условие 1,1=
<d<
=1,37 не выполняется, значит, автокорреляция присутствует.
4.2.
Для уравнения 
проверить наличие или отсутствие мультиколлинеарности.
Решение.
Используя
пункт 2.1, получаем 
0,9373 – достаточно близок к 1, значит, имеет место
мультиколлинеарность.
ЛИТЕРАТУРА
1.
Эконометрика /Под ред. Елисеевой – М.: Финансы и
статистика, 2001.
2.
Практикум по эконометрике /Под ред. Елисеевой – М.:
Финансы и статистика, 2001.
3.
Бородич С.А. Эконометрика. – Минск: Новое знание,
2001.
4.
Четыркин Е.М. Статистические методы прогнозирования. – М.: Статистика,
1975.
5.
Доугерти К. Введение в эконометрику - М.: ИНФРА-М,
1999.