Индивидуальное задание по финансовой
математике.
Вариант 18.
1. В 2003 г. в Ваш день
рождения 19.03. в банке был открыт счет до востребования на сумму 12000 рублей.
Ставка – 2% годовых, по условиям договора вклада начисление и капитализация
процентов осуществляются по истечении каждого календарного квартала. Сколько
денег получит клиент банка при закрытии счета в этот же день в 2004 году?
Решение.
Сумма после начисления
процентов в конце первого квартала 2003 года:
12000·(1+0.02·12/365)=12007.89
руб.
После 2 квартала
12007.89·(1+0.02·91/365)=12067.76
руб.
После 3 квартала
12067.76·(1+0.02·92/365)=12128.59
руб.
После 4 квартала
12128.59·(1+0.02·92/365)=12189.73
руб.
При закрытии счета
12189.73·(1+0.02·78/366)=
12241.69 руб.
2. Какой была бы эта
сумма, если бы а) начисление процентов и их капитализация осуществлялись лишь
по истечении календарного года; б) начисление процентов и их капитализация
осуществлялись бы ежедневно; в) начисление процентов и их капитализация
осуществлялись бы непрерывно?
Решение.
а) Начисление процентов в
конце года.
12000·(1+0.02·287/365)=12188.71
руб.
При закрытии счета
12188.71·(1+0.02·78/366)=
12240.66 руб.
б) Ежедневное начисление
процентов
За остаток 2003 года
12000·(1+0.02/365)287=12190.2
руб.
За период с 1 января по
18 марта 2004 года
12190.2·(1+0.02/366)78=12242.27
руб.
в) Непрерывное начисление
процентов.
За остаток 2003 года
12000·e0.02·287/365=12190.2 руб.
За период с 1 января по
18 марта 2004 года
12190.2· e0.02·78/366=12242.27 руб.
3. Дайте ответ на вопрос,
поставленный в задаче 1, если на такую же сумму в тот же день был открыт
срочный вклад на 120 дней с автоматическим продлением условий вклада на новый
срок в случае неявки клиента. Ставка – 14% годовых.
Решение.
12000·(1+0.14·120/365)3∙(1+0.02·4/366)=13737.43
руб.
4. Рассчитайте годовую
эффективную ставку процента для срочного вклада на 60 дней под 15% годовых.
Решение.

Следовательно, искомая
ставка равна 15.97%.
5. Срочный вклад на 100
дней открыт 20 августа 2002 г. На сумму 350000 рублей. Расчетная ставка – 17,2%
годовых. Какой будет величина подоходного налога (35%), уплачиваемого
вкладчиком по окончании срока вклада, если предположить, что на протяжении
всего периода ставка рефинансирования Центрального Банка останется такой же,
какой она была 20 августа?
Решение.
Сумма полученных
процентов равна
350000·(0.172·100/365)=16493.15
руб.
20 августа 2002 года
ставка рефинансирования была равна 21%.
Величина подоходного
налога
16493.15·(0.35–0.21·3/4)
= 16493.15·0.1925 = 3174.93 руб.
6. Годовая эффективная
ставка процента по срочным вкладам на год во всех банках составляет 13%. Пусть
вероятность банкротства любого банка в течении ближайшего года составляет 6%.
Банкротство банка означает потерю всех вложенных в него денег. Определите
математическое ожидание получаемой через год суммы, вероятности получить
максимум и потерять все в случае, если: а) все 900000 руб. вложены в один банк;
б) если деньги поровну распределены между двумя банками; в) если деньги поровну
распределены между тремя банками. Задачу решить в предположении, что
банкротство одних банков никак не сказывается на положении других.
Решение.
а) Возможны 2 исхода
(банк разорился, банк не разорился).
Вероятность первого
исхода – 6%. Получаемая в этом случае сумма = 0.
Вероятность второго
исхода – 94%. Получаемая в этом случае сумма = 900000·1.13 = 1017000 руб.
Математическое ожидание
получаемой суммы = 1017000·0.94 = 955980 руб.
Вероятность получить
максимум (1017000 руб.) – 94%.
Вероятность не получить
ничего – 6%.
б) Возможны 3 исхода (ни
один из банков не разорился, разорился 1 из банков, разорились оба банка).
Найдем вероятность каждого исхода и полученную в каждом случае сумму.
Вероятность того, что ни
один из банков не разорился, равна 0.942=0.8836=88.36%. Полученная
при этом сумма = 900000·1.13 = 1017000 руб.
Вероятность того, что
разорился один из банков равна 2·0.94·0.06 = 0.1128 = 11.28%. Полученная при
этом сумма 450000·1.13 = 508500 руб.
Вероятность того, что оба
банка разорились равна 0.06·0.06=0.0036 = 0.36%. Полученная при этом сумма = 0.
Математическое ожидание
получаемой суммы = 1017000·0.8836 + 508500·0.1128 = 955980 руб.
Вероятность получить
максимум (1017000 руб.) = 88.36%
Вероятность не получить
ничего = 0.36%
в) Возможны 4 исхода:
разорилось 0,1,2,3 банка. Найдем вероятность каждого исхода и полученную в
каждом случае сумму.
Вероятность того, что ни один банк не разорился, равна
0.943= 0.830584=83.0584%.
Полученная при этом сумма = 900000·1.13 = 1017000 руб.
Вероятность того, что
разорился 1 банк, равна 3·0.94·0.94·0.06 = 0.159048 = 15.9048%. Полученная при
этом сумма = 600000·1.13 = 678000 руб.
Вероятность того, что
разорились 2 банка, равна 3·0.94·0.06·0.06 = 0.010152 = 1.0152%. Полученная при
этом сумма = 300000·1.13 = 339000 руб.
Вероятность того, что все
три банка разорились равна 0.06·0.06·0.06=0.000216 = 0.0216%. Полученная при
этом сумма = 0.
Математическое ожидание
получаемой суммы = 1017000·0.830584 + 678000·0.159048 + 339000·0.010152 = 955980 руб.
Вероятность получить
максимум (1017000 руб.) = 83.0584%
Вероятность не получить
ничего = 0.0216%
7. Годовая эффективная
ставка процента по срочным рублевым вкладам – 11%. Ожидаемый рост курса доллара
в течение ближайших 12 месяцев – 13%. Определите, при каких относительных
различиях между ценами покупки и продажи в обменных пунктах имеющему доллары и
нуждающемуся через год в долларах целесообразно: а) продолжать хранить их в
наличной форме, б) поменять на рубли, открыть срочный вклад и через год
поменять возросшую рублевую сумму на доллары.
Решение.
Пусть n – отношение курса продажи к курсу
покупки, k1 – курс
доллара при покупке в начале срока. Тогда курс доллара при продаже в конце
срока (через год) будет равен k1∙n∙1.13.
S – Исходная
сумма в долларах. Продав их, мы получим S∙k1 рублей. Положив их на срочный вклад, в конце года
получим S∙k1∙1.11
рублей. Поменяв рубли на доллары мы получим (S∙k1∙1.11)/(k1∙n∙1.13)=(S∙1.11)/( n∙1.13) =S∙0.9823/n долларов.
Т.к. полученное
соотношение меньше единицы, то ни при каких условиях данная сделка выгодной не
будет.
8. Пусть сегодня в
обменных пунктах российских банков цена покупки и доллара, и евро на 3
процентных пункта меньше цены продажи (включая налог). Такой же эта разница
сохранится и в будущем. Ожидается с большой вероятностью, что ежемесячно в
течение длительного времени курс евро по отношению к доллару будет возрастать
на 0,25%. Цены покупки и продажи обеих валют будут изменяться такими же
темпами, как и биржевые курсы. Определите, целесообразно ли имеющему доллары и
нуждающемуся в перспективе в долларах обменять их на евро, а потом осуществить
обратный обмен, и если целесообразно, то в каком случае.
Решение.
Рассмотрим ситуацию,
когда человек обменял доллары на рубли, а потом рубли на евро, а по истечении n месяцев поменял их обратно.
Начальную сумму обозначим
S. Обозначим курс
покупки доллара в начале операции kd, а курс покупки евро – ke. Продав доллары, человек получил S∙kd рублей. Купив евро, человек получил (S∙kd)/(ke∙1.03) евро. Обозначим эту
сумму S1.
Прошло N месяцев. Новые курсы покупки доллара
и евро соответственно обозначим ld и le. Продав евро человек получил S1∙le рублей. Купив доллары, человек получил (S1∙le)/(ld∙1.03) долларов. Обозначив эту
сумму через S2 и выразив
ее через S получим
соотношение:

По условию задачи
соотношение 
В результате получаем
следующее соотношение:

Вся эта операция выгодна
при условии, что S2>S, т.е.
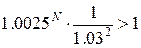



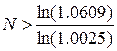
N>23.68
Т.е. целесообразно делать
эту операцию на срок 24 месяца и более.
9. Кредит на сумму 650 тыс.
руб. получен на условиях погашения его единовременным платежом вместе с
процентами через 4.5 месяца. Какую сумму должен будет возвратить заемщик
кредитору, если:
а) кредиты на такие сроки
предоставляются исходя из расчетной ставки 14% годовых, а для исчисления
стоимости кредита используется формула простых процентов;
б) для кредитов на любые
сроки используется годовая эффективная ставка – 14%?
Решение.
а)
650000·(1+0.14·4.5/12)=684125 рублей.
б) 650000·(1+0.14)4.5/12=682735.8
рублей.
10. Какие суммы должен
ежемесячно отдавать заемщик кредитору, если бы погашение кредита
предусматривалось двумя равными суммами – соответственно через 2.5 месяца и 4.5
месяца, если:
а) расчетная ставка
остается такой же, как в задаче 9, и для соизмерения денежных сумм во времени
используется формула простых процентов;
б) годовая эффективная
ставка остается такой же, как в задаче 9, и для соизмерения денежных сумм во
времени используется формула сложных процентов?
Решение.
а) Обозначим искомую
сумму x.
Получим соотношение.
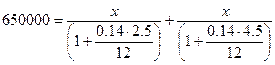
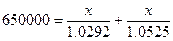

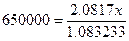


x=338233.87
б) Обозначим искомую
сумму x.
Получим соотношение.
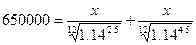

650000=0.973∙x+0.952∙x
650000=1.925∙x
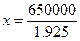
x=337662.34
11. Какую сумму в
условиях задачи 9 получил бы на руки заемщик, если бы кредитор взял с него
проценты в момент выдачи кредита?
Решение.
650000/(1+0.14·4.5/12)=617577.2
руб.
12. Фирма обязана
выплачивать 1-го числа каждого месяца 1.5 млн. руб. в течении 15 месяцев.
Замените это обязательство финансово эквивалентным, если сроки всех выплат
отодвигаются на 20 дней, а для соразмерения денежных сумм во времени
используется годовая эффективная ставка 18%.
Решение.
За двадцать дней каждый
платеж возрастет в 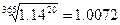 раза и составит
1500000∙1.0072=1510800 рублей.
раза и составит
1500000∙1.0072=1510800 рублей.
13. Кредиты на 5 месяцев
выдаются, исходя из расчетной ставки 25% годовых. Исходя из какой расчетной
ставки должны выдаваться кредиты на 1 месяц, чтобы годовая эффективная ставка
процента по таким кредитам была такой же, как и по кредитам на 5 месяцев?
Решение.

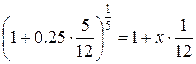

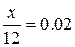
x=0.24
Получаем расчетную ставку
24%.
14. Банк предоставляет
рублевые кредиты сроком на 2 года на следующих условиях: расчетная ставка
составляет 24% годовых, основной долг необходимо погашать ежемесячно двадцатью
четырьмя равными частями с одновременной уплатой процентов за пользование той
суммой денег, которую заемщик был должен в течении последнего месяца. На
аналогичных условиях, исходя из ставки 12% годовых, предоставляются кредиты в
долларах США. Определите денежные суммы, которые: а) необходимо ежемесячно
возвращать банку получившему рублевый кредит в размере 1.2 млн. руб.; б)
необходимо ежемесячно возвращать банку получившему кредит в долларах на такую
же сумму в 1.2 млн. руб. В случае б) рассчитайте рублевые эквиваленты
возвращаемых сумм. В обоих случаях рассчитайте величины 2 первых и двух
последних платежей. На момент получения
кредита курс доллара составляет 30 руб., ежемесячно он увеличивается на 0.5%.
Решение.
а) Рассчитаем сумму,
которую необходимо вернуть в банк в конце каждого месяца. Эта сумма состоит из
двух частей. Первая – часть долга. Она постоянна и составляет 1200000/24=50000
рублей. Вторая – проценты за пользование той суммой денег, которую заемщик был
должен в течении последнего месяца. Эта сумма составляет (1200000–50000·(N–1))·0.02, где N – номер прошедшего месяца.
Таким образом, величина
платежа после первого месяца составит 50000+1200000·0.02=50000+24000=74000
рублей.
Величина второго платежа
составит
50000+(1200000–50000)·0.02=50000+(24000–1000)=73000
рублей.
Величина предпоследнего
платежа составит
50000+(1200000–50000·22)·0.02=50000+100000·0.02=52000
рублей.
Величина последнего
платежа составит
50000+(1200000–50000·23)·0.02=50000+50000·0.02=51000
рублей.
б) Переведя сумму заема в
доллары по начальному курсу получим сумму
в 40000 долларов. Рассчитаем сумму, которую необходимо вернуть в банк в
конце каждого месяца. Эта сумма состоит из двух частей. Первая – часть долга.
Она постоянна и составляет 40000/24=1666.67 долларов. Вторая – проценты за
пользование той суммой денег, которую заемщик был должен в течении последнего
месяца. Эта сумма составляет (40000–1666.67·(N–1))·0.01, где N – номер прошедшего месяца.
Для нахождения рублевого
эквивалента отдаваемых сумм необходимо умножить сумму в долларах на курс
доллара в текущем месяце. Он будет равен 30·(1+0.005)N, где N – номер прошедшего месяца. Таким
образом рублевый эквивалент суммы, отдаваемой после N-го месяца будет равен (1666.67+(40000–1666.67·(N–1))·0.01) ·30·(1+0.005)N.
Таким образом, величина
платежа после первого месяца составит
(1666.67+40000·0.01) =
2066.67 долларов или 2066.67·30·(1+0.005) = 62310.10 рублей
Величина второго платежа
составит
(1666.67 + ((40000–1666.67)·0.01))
= 1666.67+383.33 = 2050 долларов или 2050·30·(1+0.005)2 = 62116.54
рублей
Величина предпоследнего
платежа составит
(1666.67 +
((40000–1666.67·22)·0.01)) = 1666.67+33.33 = 1700 долларов или
1700·30·(1+0.005)23 = 57199.15 рублей
Величина последнего
платежа составит
(1666.67 +
((40000–1666.67·23)·0.01)) = 1666.67+16.67 = 1683.34 долларов или 1683.34·30·(1+0.005)24
= 56921.79 рублей
15. Фирме Х была
предоставлена кредитная линия на 2 млн. рублей – в течение 10 месяцев по 1-м
числам она брала в банке по 200 тыс. руб. Погашение долга предусматривалось
единовременным платежом ровно через 7 месяцев после получения последних 200
тысяч. Сколько должна вернуть фирма банку, если для соизмерения денежных сумм
во времени используется годовая эффективная ставка 16%.
Решение.
После получения
последнего кредита задолженность фирмы перед банком составляла:
200000∙(1+(1+0.16/12)+(1+0.16/12)2+…+(1+0.16/12)9)
= по формуле суммы геометрической прогрессии =  = 2124367.83
= 2124367.83
После 7 месяцев задолженность
составит
2124367.83*(1+0.16/12)7=2124367.83*1.097=2330431.51
руб.
16. Номинал дисконтной
облигации составляет 50000 рублей. Годовая эффективная ставка процента на
денежном рынке – 17%. Сегодня 10 мая, Дата погашения облигации – 1 августа
следующего года. Определите формальную рыночную цену такой облигации на
сегодняшний день. Какой будет ее цена через 6 месяцев, т.е. 10 ноября. С какого
дня рыночная цена облигации превысит 46000 рублей?
Решение.
На сегодняшний день до
погашения облигации остается 446 дней.
Формальная рыночная цена
на сегодняшний день.
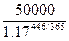 =
= 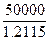 = 41271.15 руб.
= 41271.15 руб.
На 10 ноября до погашения
облигации остается 262 дня.
Формальная рыночная цена
на 10 ноября.
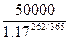 =
=  = 44595.08 руб.
= 44595.08 руб.
Найдем количество дней до
погашения, при котором формальная рыночная стоимость облигации превысит 46000
рублей.
Обозначим искомое
количество дней N.
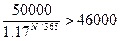
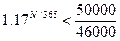

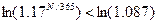
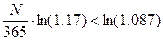

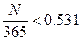

Следовательно, формальная
рыночная стоимость облигации превысит 46000 рублей за 193 дня до погашения.
Случится это 18 января.
17. Рассчитайте формальную
рыночную стоимость акций, по которым ежегодно выплачиваются дивиденды в размере
250 руб. на одну акцию. Годовая эффективная ставка процента составляет 13%.
Цену рассчитать для момента, когда до получения очередного дивиденда остается
ровно семь месяцев.
Решение.
Стоимость акции сразу
после выплаты дивидендов –  1923.08 руб.
1923.08 руб.
В день выплаты дивидендов
стоимость акции будет равна 1923.08+250=2173.08 руб.
Для момента, когда до
уплаты дивиденда остается семь месяцев, т.е. через 5 месяцев после выплаты
стоимость акции составит

18. При какой годовой
эффективной ставке процента на денежном рынке максимальная рыночная стоимость
консоли, позволяющей ее владельцу получать ежегодно получать 500 рублей,
составит 6000 рублей.
Решение.
Обозначим искомую ставку x. Получим:
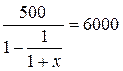
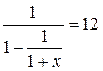
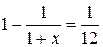



19. С каким дисконтом
банк должен учесть вексель, срок погашения которого – через 4.5 месяца, чтобы
доходность этой операции была такой же, как при выдаче кредита на такой же
срок, исходя из расчетной ставки 18% годовых?
Решение.
Рассчитаем доходность
кредита на на 4.5 месяца при расчетной ставке 18% годовых.
0.18∙4.5/12=0.0675=6.75%.
Доходность вексельной
операции будет также 6.75%, следовательно с таким дисконтом банк и должен
учесть вексель в предлагаемых условиях.
20. В течении года
проводится 10 тиражей лотереи, где обладатели счастливых билетов получают
квартиры. Пусть выигрывает 1 билет из 1000. Вы имеете деньги, достаточные для
приобретения 10 лотерейных билетов. Можно поучаствовать лишь в одном тираже,
купив сразу 10 билетов. Можно поучаствовать в 10 тиражах, приобретая каждый раз
по 1 билету. В каком случае вероятность стать собственником квартиры больше?
Если Вы считаете, что для решения задачи необходима дополнительная информация,
придумайте ее сами.
Решение.
Найдем вероятность хотя
бы выигрыша при покупке в 10 тиражах по одному билету.
Вероятность выигрыша
одного купленного билета в тираже равна 0.001.
Для упрощения расчетов
найдем вероятность дополнительного события, т.е. вероятность того, что ни один
из билетов не выиграл. Эта вероятность будет равна 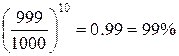 . Искомая вероятность соответственно равна 1–0.99=0.01=1%.
. Искомая вероятность соответственно равна 1–0.99=0.01=1%.
Найдем вероятность
выиграть хотя бы один раз при покупке 10 билетов в одном тираже.
Обозначим N – количество выигрышных билетов.
Общее число билетов – 1000∙N
Для упрощения расчетов
найдем вероятность дополнительного события, т.е. вероятность того, что ни один
из билетов не выиграл.
Вероятность того, что
первый билет участника не выиграл равна  . Вероятность того,
что второй билет участника не выиграл равна
. Вероятность того,
что второй билет участника не выиграл равна 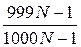 . Вероятность того, что k-й билет участника не выиграл равна
. Вероятность того, что k-й билет участника не выиграл равна 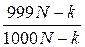 . С каждым последующим билетом вероятность проигрыша
уменьшается, т.к.
. С каждым последующим билетом вероятность проигрыша
уменьшается, т.к. 
Из приведенных расчетов
следует, что вероятность стать собственником квартиры во втором случае (купив
10 билетов в одном тираже) несколько выше.
21. Купонные облигации
сразу после их эмиссии продаются по номиналу. Владельцы этих облигаций имеют
право через каждые 3 месяца получать доход в размере 5% от номинала. Каждая
облигация имеет 8 купонов. По истечении 2 лет владельцу облигации наряду с
процентами по последнему купону выплачивается и номинальная стоимость
облигации. Будут ли эти облигации пользоваться большим спросом, если на
денежном рынке годовая эффективная ставка составляет 20%.
Решение.
Обозначим номинал
облигации S.
Данные облигации будут
пользоваться спросом, если доходы ее владельца, приведенные к настоящему
времени составят величину, большую, чем ее номинальная стоимость, за которую он
ее приобрел.
Найдем сумму этих
доходов.
Современная стоимость
номинала облигации, полученной владельцем через 2 года составит  = 0.6944·S
= 0.6944·S
Кроме того, каждый
квартал владелец облигации получает доход в размере 0.05·S. Доходы после i-го квартала, приведенные к
настоящему времени составят 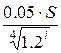 . Доходы от процентов, приведенные к настоящему времени
составят
. Доходы от процентов, приведенные к настоящему времени
составят  =
=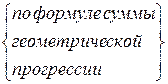 =
=  =
=  =
=  = 0.3276·S
= 0.3276·S
Итого искомые доходы составят
0.6944·S+0.3276·S=1.022·S
Следовательно, данные
облигации обеспечивают реальный доход 2.2%, и по идее должны пользоваться
спросом.
22. Номинальная годовая
эффективная ставка процента на денежном рынке составляет 28%. Чему равна
реальная ставка процента, если рост среднего уровня цен за год составляет: а)
16%; б) 25%; в) 45%.
Решение.
 , где i – реальная ставка процента, r – номинальная ставка, h – рост среднего уровня цен.
, где i – реальная ставка процента, r – номинальная ставка, h – рост среднего уровня цен.
а) 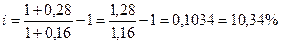
б) 
в) 
23. Определите с позиций
формальной финансовой математики, при какой годовой эффективной ставке процента
по депозитам выгоднее покупать ежегодно туфли по цене 1500 рублей, чем раз в
три года – туфли по цен 4300 рублей. Внешний вид и потребительские свойства у
них одинаковы, различается только срок службы.
Решение.
[(4300–1500)(1+r)–1500](1+r)≥1500
[2800(1+r)–1500](1+r)≥1500
[28(1+r)–15](1+r)≥15
28(1+r)2–15(1+r)–15≥0
D=225+1680=1905
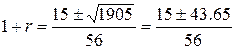
Отрицательный корень отбрасываем
по условию задачи
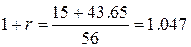
r≥0.047
Получается, что первые
туфли выгоднее покупать, когда годовая эффективная ставка процента больше, чем 4.7%.
24. Семья арендует
квартиру и платит за нее ежемесячно 3500 руб. Текущие доходы семьи позволяют
ежемесячно откладывать 4000 руб. (остальные деньги уходят на неотложные нужды и
арендатору). Есть мечта приобрести собственную квартиру стоимостью 600000 руб.
Предположив, что деньги накапливаются в наличной форме, определите,
целесообразно ли для ускорения решения проблемы прибегнуть к банковскому
кредиту, который на любые сроки выдается из расчета годовой эффективной ставки
9%, и если целесообразно, то когда (после накопления какой суммы собственных
средств) это лучше всего сделать? После покупки квартиры можно будет отдавать
кредитору 7500 руб. ежемесячно.
Решение.
Обозначим t – количество месяцев, в течении
которых семья накапливает деньги. После этого они берут кредит, в размере (600000–4000t) рублей. Обозначим n – число месяцев в течении которых
они погасят кредит. Получаем соотношение:

В правой части равенства
стоит геометрическая прогрессия.
Найдем ее сумму по
формуле 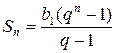
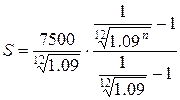 =
=  =
=  =
=  =
=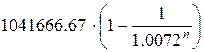 =
= 
В итоге получаем
соотношение:
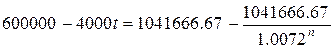
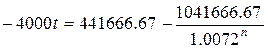

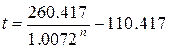
Нам надо найти решение,
при котором t+n→min.
Выразив t через n получим задачу нахождения наименьшего
значения функции одной переменной.

Найдем производную данной
функции.
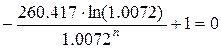
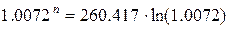
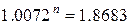
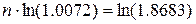

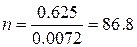
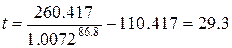
Так как получено дробное
решение, то для нахождения ответа необходимо проверить два ближайших целых.
При t=30 объем займа составит 480000
рублей. Решим уравнение относительно n.
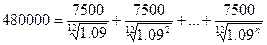
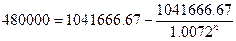
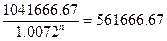
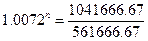
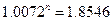
n∙ln(1.0072)=ln(1.8546)

n=86.1
Полное погашение кредита
возможно через 87 месяцев.
При t=29 объем займа составит 484000
рублей. Решим уравнение относительно n.

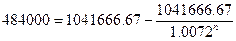
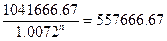
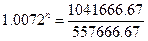
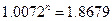
n∙ln(1.0072)=ln(1.8679)
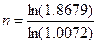
n=87.1
Полное погашение кредита
возможно через 88 месяцев.
И в том и в другом случае
семья становится собственником квартиры через 117 месяцев.
25. Дайте определения по
следующим понятиям:
а) сберегательный
сертификат - ценная бумага, удостоверяющая сумму вклада, внесенного в банк, и
права вкладчика (держателя сертификата) на получение по истечении
установленного срока суммы вклада и обусловленных в сертификате процентов в
банке, выдавшем сертификат, или в любом филиале этого банка;
б) депозитарная расписка -
документ, удостоверяющий, что ценные бумаги помещены на хранение в депозитарии
банка;
в) финансовый лизинг -
операция по специальному приобретению имущества в собственность и последующей
сдачей его во временное владение и пользование на срок, приближающийся по
продолжительности к сроку эксплуатации и амортизации всей стоимости имущества.
В течение срока договора лизингодатель за счет лизинговых платежей возвращает
себе всю стоимость имущества и получает прибыль от финансовой сделки.
Фактически финансовый лизинг представляет собой форму долгосрочного
кредитования. Финансовый лизинг характеризуется трехсторонним характером
взаимоотношений;
г) привилегированная
акция - акция, которая не дает права голоса, если иное не предусмотрено уставом
акционерного общества.
Выплаты дивидендов по
привилегированным акциям производятся после выплат на облигации и до выплат по
обыкновенным акциям. Обычно по привилегированным акциям владельцу гарантируется
фиксированный размер дивиденда (в процентах к номинальной стоимости акции).
Различают кумулятивные,
некумулятивные и привилегированные акции с участием;
д) американский опцион -
опцион, который может быть предъявлен к исполнению в любое время до окончания
срока его действия;
е) двойное складское
свидетельство - Документ, выдаваемый товарным складом в подтверждение того, что
товар находится на складе.
Двойное складское
свидетельство состоит из двух частей - складского свидетельства и залогового
свидетельства (варранта), которые могут быть отделены одно от другого.
Двойное складское
свидетельство, каждая из двух его частей свидетельство являются ценными
бумагами.
Товар, принятый на
хранение по двойному складскому свидетельству, может быть в течение его
хранения предметом залога.