12. График погашения
кредита предполагал ежемесячную выплату заемщиком 1 млн. руб. в течение 8
месяцев (1-й платеж – через месяц после получения кредита, второй – через 2
месяца и т.д.). После совершения 5 платежей заемщик решил рассчитаться с
кредитором досрочно – по истечении 6-го месяца полностью погасить остаток
долга. Сколько он должен будет заплатить кредитору по истечении 6-го месяца при
условии, что фактические платежи будут финансово эквивалентными первоначальным
обязательствам, а для соизмерения денежным сумм во времени используется годовая
эффективная ставка 25%?
Решение.
Необходимо найти сумму
платежа, эквивалентного восьми платежам по 1000000 рублей с перерывом 1 месяц между
платежами при годовой эффективной ставке 25%:
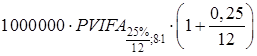 =1000000·
=1000000·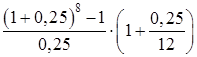 =
=20255229,95 руб.
=
=20255229,95 руб.
Также найдем сумму,
эквивалентную пяти платежам по 1000000 рублей с перерывом 1 месяц между
платежами при годовой эффективной ставке 25%:
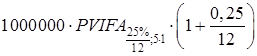 =1000000·
=1000000·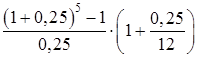 =
=8378011,068 руб.
=
=8378011,068 руб.
Искомая сумма составит:
20255229,95 – 8378011,068 = 11877218,88 руб.
13. Кредиты на 2 месяца
выдаются, исходя из расчетной ставки 22% годовых. Исходя из какой расчетной
ставки должны выдаваться кредиты на 6 месяцев, чтобы годовая эффективная ставка
процента по таким кредитам была такой же, как и по кредитам на 2 месяца?
Решение.
Рассчитаем сумму Р
возврата для суммы кредита S при расчетной ставке 22%.
P=S·(1+0,22·2/12) = S·1,037.
Определим годовую
эффективную ставку процентов, при которой прирост средств за 6 месяцев будет
такой же.
P=S·
(1+х)6/12 = S·1,013, где х – искомая процентная
ставка.
(1+х)1/2=1,037.
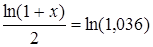
ln(1+х)=2·ln(1,036)
ln(1+х)=0,035
1+х=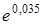 =1,0356
=1,0356
х=0,0356, т.е.
3,56%
Определим прирост средств
за 1 месяц при вычисленной эффективной ставке:
(1+0,0356)1/12=1,003.
Вычислим расчетную
ставку, при которой будет такой же прирост.
1+х·1/12=1,003.
х=0,036, т.е. 3,6%.
14. Фирме Х была
предоставлена кредитная линия на 1 млн. рублей – в течение 6 месяцев по 1-м
числам она брала в банке по 200 тыс. руб. Погашение долга предусматривалось
единовременным платежом ровно через 5 месяцев после получения последних 200
тысяч. Сколько должна вернуть фирма банку, если для соизмерения денежных сумм
во времени используется годовая эффективная ставка 13%.
Решение.
После получения
последнего кредита задолженность фирмы перед банком составляла:
200000·FVIFA13%/12;5·(1+0.13/12)=2000000·5,109·1,0108=1032835,44
руб.
После 5 месяцев
задолженность составит
1032835,44·(1+0,13/12)5=1032835,44·1,05518=1089827,3
руб.
15. Единовременно
полученный кредит сроком на 3 года погашался в течение этого срока ежемесячно
равными суммами. Для соизмерения денежных сумм во времени использовалась
годовая эффективная ставка R. После завершения последнего, 36-го платежа, заемщик
обнаружил, что в сумме он заплатил банку ровно в 1,5 раза больше, чем брал у
него взаймы. Каково было значение годовой эффективной ставки?
Решение.
Обозначим S сумму взятого кредита. За год было
отдано 0,5S.
PVIFAR;3=2.
Подбором находим R=23,4%.
16. Облигации внутреннего
выигрышного займа выпущены на следующих условиях. Всего облигаций 20 млн. штук,
срок погашения – через 10 лет. Ежегодно в конце каждого календарного квартала
проводится тираж, в результате которого 20000 облигаций выигрывают. Выигравшие
облигации в дальнейших тиражах не участвуют. Определите вероятность выигрыша в
первых трех тиражах хотя бы одной облигации для человека, купившего 20
облигаций.
Решение.
Рассчитаем вероятность
того, что в трех тиражах ни одна из 20 акций не выиграла. Тогда искомая
вероятность будет равна 1 минус найденная вероятность.
Возьмем первый тираж.
Вероятность выигрыша каждой конкретной акции составляет 1/1000. Вероятность не
выигрыша каждой конкретной акции 999/1000. Вероятность того, что ни одна из 20
облигаций не выиграет равна 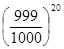 . Аналогично для второго тиража получим вероятность того, что
ни одна из 20 облигаций не выиграет
. Аналогично для второго тиража получим вероятность того, что
ни одна из 20 облигаций не выиграет 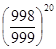 , т.к. выигравшие в первом тираже акции в дальнейших тиражах не
участвуют. Из тех же соображений для
третьего тиража получим вероятность того, что ни одна из 20 облигаций не
выиграет
, т.к. выигравшие в первом тираже акции в дальнейших тиражах не
участвуют. Из тех же соображений для
третьего тиража получим вероятность того, что ни одна из 20 облигаций не
выиграет 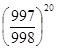 . Для того, что бы акция не выиграла ни в одном из трех
тиражей эти события должны произойти одновременно, т.е. для нахождения этой
вероятности необходимо перемножить все три найденных значения. В итоге получим
вероятность того, что ни одна акция из 20 не выиграет в первых трех тиражах
. Для того, что бы акция не выиграла ни в одном из трех
тиражей эти события должны произойти одновременно, т.е. для нахождения этой
вероятности необходимо перемножить все три найденных значения. В итоге получим
вероятность того, что ни одна акция из 20 не выиграет в первых трех тиражах 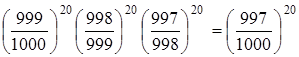 =0,94168.
=0,94168.
Вероятность того, что
хотя бы одна из 20 акций выиграет в первых трех тиражах равна
1–0,94168=0,05832, т.е. 5,832%.
17. Определите стартовую
формальную рыночную цену купонной облигации (всего купона) номиналом 1 млн.
руб., погашаемой через 1 год, по которой по истечении каждых трех месяцев
выплачивается доход в размере 6% от номинала. Годовая эффективная ставка
процента на денежном рынке составляет 15%.
Решение. Обозначим
искомую цену через S. Получим условие.
S·1,24·1,15=1000000.
S=701262,27
руб.
20. Продаются лотереи
двух номиналов – по 100 рублей и по 10 рублей. «Дорогих» билетов всего 200 и из
них выиграют лишь два, «дешевых» - 2000 и из них выиграют тоже лишь два билета.
Размеры выигрыша одинаковы. Одинакова ли будет вероятность выиграть у купившего
1 «дорогой» билет и у купившего 10 «дешевых»?
Решение. Вероятность
выиграть у человека, купившего 1 «дорогой» билет равна 2/200=0,01, т.е. 1%.
Найдем теперь вероятность
выиграть у человека, купившего 10 «дешевых» билетов. Вероятность того, что
конкретны билет выиграл равна 1/1000, а вероятность того, что конкретный билет
не выиграл равна 999/1000. Вероятность того, что из 10 билетов ни один не
выиграл, равна
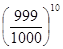 = 0,99.
Соответственно, вероятность выигрыша хотя бы одного из 10 «дешевых» билетов
равна 1–0,99=0,01, т.е. 1%.
= 0,99.
Соответственно, вероятность выигрыша хотя бы одного из 10 «дешевых» билетов
равна 1–0,99=0,01, т.е. 1%.
22. Семья арендует
квартиру и платит за нее ежемесячно 2500 руб. Текущие доходы семьи позволяют
ежемесячно откладывать 5000 руб. (остальные деньги уходят на неотложные нужды и
арендатору). Есть мечта приобрести собственную квартиру стоимостью 500000 руб.
Предположив, что деньги накапливаются в наличной форме, определите,
целесообразно ли для ускорения решения проблемы прибегнуть к банковскому
кредиту, который на любые сроки выдается из расчета годовой эффективной ставки
8%, и если целесообразно, то когда (после накопления какой суммы собственных
средств) это лучше всего сделать? После покупки квартиры можно будет отдавать
кредитору 7500 руб. ежемесячно.
Решение.
Рассчитаем расходы семьи
на протяжении всего периода накопления денег и расчета с кредитором, исходя из
условия, что после того, как семья N месяцев копила деньги, она взяла
кредит и приобрела квартиру.
За N месяцев семья накопила 5000N рублей. Так же за эти N месяцев семья заплатила 2500N рублей в качестве арендной платы за
квартиру. Для приобретения квартиры им пришлось взять кредит в сумме P=500000–5000N рублей. После этого до полного
расчета они платили кредитору 7500 рублей ежемесячно.
Рассчитаем количество
месяцев (n), в течении которого семья расплачивалась за кредит, из уравнения
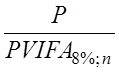 =7500.
=7500.
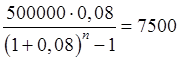
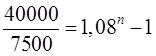
23. Определите с позиций
формальной финансовой математики, при какой годовой эффективной ставке процента
по депозитам выгоднее купить телевизор стоимостью 8000 рублей сроком службы 8
лет по сравнению с телевизором стоимостью 5000 рублей сроком службы 4 года.
Прочие характеристики обоих телевизоров одинаковы.
Решение.
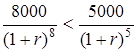
8<5·(1+r)3
(1+r)3>1,6
1+r>1,1696
r>0,1696
Получается, что первый
телевизор выгоднее покупать, когда годовая эффективная ставка процента больше,
чем 16,96%.
24. Определите формальную
рыночную цену ежемесячной вечной ренты в 2000 рублей, если годовая эффективная
ставка процента на денежном рынке составляет 6%.
Решение.
Искомая цена 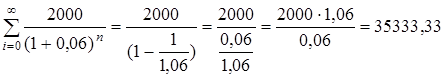 руб.
руб.
25. Дайте определения по
следующим понятиям:
г) аннуитет – вид
периодической уплаты фиксированной или варьирующейся суммы, вытекающей из
контрактных обязательств;
д) рента постнумерандо
(обыкновенная рента) – Рента, выплачиваемая в конце каждого периода, установленного
для очередной выплаты страхового обеспечения;
е) ставка ЛИБОР (LIBOR) – Лондонская межбанковская ставка
предложения. Шкала процентных ставок, которые применяются лондонскими банками,
выступающими на евровалютном межбанковском рынке с предложением средств в
разных евровалютах и на разные сроки: 1, 2, 6 и 12 месяцев. Каждый крупный
лондонский банк самостоятельно устанавливает и изменяет ставку ЛИБОР в
зависимости от складывающейся конъюнктуры на валютном рынке.