Задание 1.
Вариант 8.
Дано: n=32 выборочных значений c величины X > N(a,σ) – таблица.
Требуется:
1. Построить
гистограмму и полигон приведенных частот (число интервалов k выбрать
согласно формуле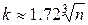 
).
2. Найти
оценки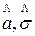 
, асимметрия a,
эксцесс e.
3. Для
параметров a, σ найти
доверительные интервалы с надежностью 0.95.
4. Сравнить
выборочные характеристики с соответствующими кривыми нормального распределения,
для чего написать выражения для оценок
функций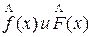 
и построить графики
этих функций по точкам.
5. Найти
эмпирическую функцию распределения Fn(x)
и построить ее график на одном чертеже с графиком функции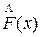 
.
6. По величине
асимметрии a и эксцессу
e сделать
заключение (предварительное) о нормальности распределения c величины X.
7. Проверить с
помощью Критерия χ2 (хи-квадрат) гипотезу о нормальности распределения
генеральной совокупности. Уровень значимости выбрать α=0.05
Исходные
данные.
|
0.041
|
–0.307
|
0.121
|
0.790
|
-0.584
|
0.541
|
0.484
|
–0.986
|
|
–1.132
|
–2.098
|
0.921
|
0.145
|
0.446
|
–1.661
|
1.045
|
–1.363
|
|
0.768
|
0.079
|
–1.473
|
0.034
|
–2.127
|
0.665
|
0.084
|
–0.880
|
|
0.375
|
–1.658
|
–0.851
|
0.234
|
–0.656
|
0.340
|
–0.086
|
–0.158
|
Решение.
1. Число
интервалов равно 1.72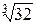
= 5.46 ≈ 5.
Границы
интервалов и число попавших в них значений.
1-й интервал:
(-2.127;-1.4926) – 4
2-й интервал:
(-1.4926;-0.8582) – 5
3-й интервал:
(-0.8582;-0.2238) – 4
4-й интервал:
(-0.2238;0.4106) – 11
5-й интервал:
(0.4106;1.045) – 8
2. 
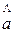= (0.041- 0.307+
0.121+ 0.79- 0.584+ 0.541+ 0.484- 0.986- 1.132- 2.098+ 0.921+ 0.145+ 0.446-
1.661+ 1.045- 1.363+ 0.768+ 0.079- 1.473+ 0.034- 2.127+ 0.665+ 0.084- 0.88+
0.375- 1.658- 0.851+ 0.234- 0.656+ 0.34- 0.086- 0.158)/32=–0.2782
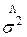= ((0.041+0.2782)2+
(-0.307+0.2782)2+ (0.121+0.2782)2+ (0.79+0.2782)2+
(-0.584+0.2782)2+ (0.541+0.2782)2+ (0.484+0.2782)2+
(-0.986+0.2782)2+ (-1.132+0.2782)2+ (-2.098+0.2782)2+
(0.921+0.2782)2+ (0.145+0.2782)2+ (0.446+0.2782)2+
(-1.661+0.2782)2+ (1.045+0.2782)2+ (-1.363+0.2782)2+
(0.768+0.2782)2+ (0.079+0.2782)2+ (-1.473+0.2782)2+
(0.034+0.2782)2+ (-2.127+0.2782)2+ (0.665+0.2782)2+
(0.084+0.2782)2+ (-0.88+0.2782)2+ (0.375+0.2782)2+
(-1.658+0.2782)2+ (-0.851+0.2782)2+ (0.234+0.2782)2+
(-0.656+0.2782)2+ (0.34+0.2782)2+ (-0.086+0.2782)2+
(-0.158+0.2782)2)/32 = (0.101889+ 0.000829+ 0.159361+ 1.141051+
0.093514+ 0.671089+ 0.580949+ 0.500981+ 0.728974+ 3.311672+ 1.438081+ 0.179098+
0.524466+ 1.912136+ 1.750858+ 1.176791+ 1.094534+ 0.127592+ 1.427547+ 0.097469+
3.418061+ 0.889626+ 0.131189+ 0.362163+ 0.42667+ 1.903848+ 0.3281+ 0.262349+
0.142733+ 0.382171+ 0.036941+ 0.014448)/32 = 0.7912
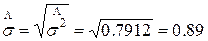
Найдем
центральные моменты выборки.
Момент второго
порядка – это дисперсия.
μ2 = 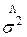= 0.7912
Момент
третьего порядка.
μ3 = ((0.041+0.2782)3+
(-0.307+0.2782)3+ (0.121+0.2782)3+ (0.79+0.2782)3+
(-0.584+0.2782)3+ (0.541+0.2782)3+ (0.484+0.2782)3+
(-0.986+0.2782)3+ (-1.132+0.2782)3+ (-2.098+0.2782)3+
(0.921+0.2782)3+ (0.145+0.2782)3+ (0.446+0.2782)3+
(-1.661+0.2782)3+ (1.045+0.2782)3+ (-1.363+0.2782)3+
(0.768+0.2782)3+ (0.079+0.2782)3+ (-1.473+0.2782)3+
(0.034+0.2782)3+ (-2.127+0.2782)3+ (0.665+0.2782)3+
(0.084+0.2782)3+ (-0.88+0.2782)3+ (0.375+0.2782)3+
(-1.658+0.2782)3+ (-0.851+0.2782)3+ (0.234+0.2782)3+
(-0.656+0.2782)3+ (0.34+0.2782)3+ (-0.086+0.2782)3+
(-0.158+0.2782)3)/32 = (0.032523- 0.000024+ 0.063617+ 1.218871-
0.028596+ 0.549756+ 0.442799- 0.354594- 0.622398- 6.026581+ 1.724546+ 0.075794+
0.379818- 2.644101+ 2.316736- 1.276583+ 1.145102+ 0.045576- 1.705633+ 0.03043-
6.319312+ 0.839095+ 0.047517- 0.21795+ 0.278701- 2.62693- 0.187936+ 0.134375-
0.053924+ 0.236258+ 0.0071+ 0.001737)/32 = -0.390443
Момент
четвертого порядка.
μ4 = ((0.041+0.2782)4+
(-0.307+0.2782)4+ (0.121+0.2782)4+ (0.79+0.2782)4+
(-0.584+0.2782)4+ (0.541+0.2782)4+ (0.484+0.2782)4+
(-0.986+0.2782)4+ (-1.132+0.2782)4+ (-2.098+0.2782)4+
(0.921+0.2782)4+ (0.145+0.2782)4+ (0.446+0.2782)4+
(-1.661+0.2782)4+ (1.045+0.2782)4+ (-1.363+0.2782)4+
(0.768+0.2782)4+ (0.079+0.2782)4+ (-1.473+0.2782)4+
(0.034+0.2782)4+ (-2.127+0.2782)4+ (0.665+0.2782)4+
(0.084+0.2782)4+ (-0.88+0.2782)4+ (0.375+0.2782)4+
(-1.658+0.2782)4+ (-0.851+0.2782)4+ (0.234+0.2782)4+
(-0.656+0.2782)4+ (0.34+0.2782)4+ (-0.086+0.2782)4+
(-0.158+0.2782)4)/32 = (0.010381+ 0.000001+ 0.025396+ 1.301998+
0.008745+ 0.45036+ 0.337502+ 0.250982+ 0.531404+ 10.967172+ 2.068076+ 0.032076+
0.275064+ 3.656263+ 3.065505+ 1.384837+ 1.198006+ 0.01628+ 2.037891+ 0.0095+
11.683144+ 0.791435+ 0.017211+ 0.131162+ 0.182047+ 3.624637+ 0.10765+ 0.068827+
0.020373+ 0.146055+ 0.001365+ 0.000209)/32 = 1.387548
Коэффициент
Асимметрии.
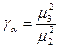= (-0.390443)2/0.7911622
= 0.152445736249/0.625937310244 = 0.152446
Эксцесс.
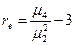= 1.387548/0.7911622–3
= 1.387548/0.625937310244–3 = –1.612451
3. Границы
доверительного интервала для a.
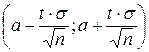, где
2·Ф(t)=0.95
Ф(t)=0.475
t=1.96
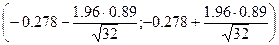
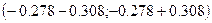
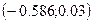
Границы
доверительного интервала для σ.
(σ∙(1-q(γ,n)); σ∙(1+q(γ,n)))
(0.89∙(1-q(0.95,32)); 0.89∙(1+q(0.95,32)))
(0.89∙(1-0.27);
0.89∙(1+0.27))
(0.89–0.24; 0.89+0.24)
(0.65; 1.13)
4. 
= 
= 
= 
= 
= 
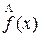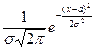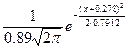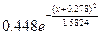
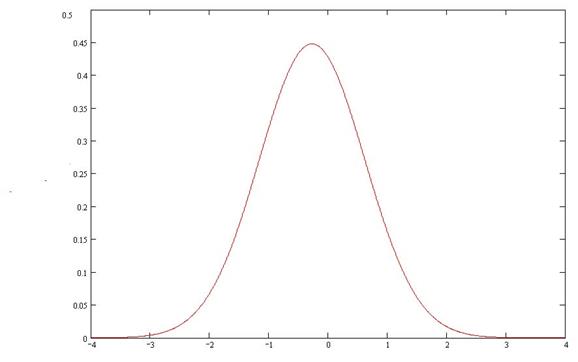
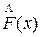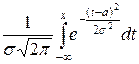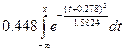
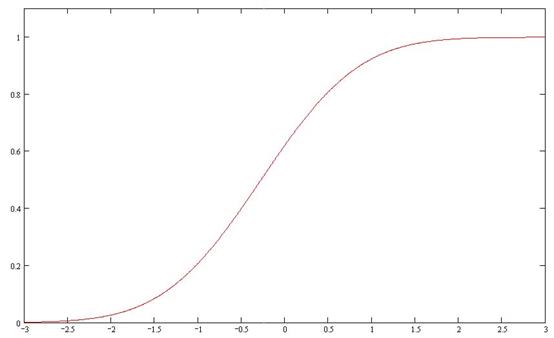
5. Эмпирическая
функция распределения Fn(x)
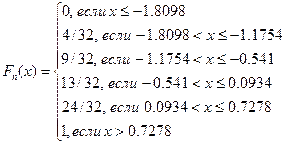
Построим
график этой функции на одном чертеже с графиком функции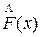
6. Т.к.
Коэффициент асимметрии достаточно мал, то можно сделать предположение о
нормальном распределении величины X.
7. Таблица
частот:
1-й интервал:
(-2.127;-1.4926) – 4
2-й интервал:
(-1.4926;-0.8582) – 5
3-й интервал:
(-0.8582;-0.2238) – 4
4-й интервал:
(-0.2238;0.4106) – 11
5-й интервал:
(0.4106;1.045) – 8
Таблица
относительных частот середин интервалов.
– 1.8098 –
4/32 = 0.125
– 1.1754 –
5/32 = 0.15625
– 0.541 – 4/32
= 0.125
0.0934 – 11/32
= 0.34375
0.7278 – 8/32
= 0.25
Найдем
вероятности:
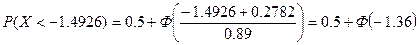= 0.5–Ф(1.36) =
0.5–0.4131 = 0.0869
P(–1.4926<X<–0.8582) =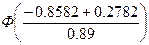 
– 
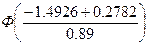= Ф(–0.65) –
Ф(–1.36) = Ф(1.36) – Ф(0.65) = 0.4131 – 0.2422 = 0.1709
P(–0.8582<X<–0.2238) =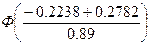 
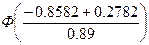– = Ф(0.06) –
Ф(–0.65) = Ф(0.06) + Ф(0.65) = 0.0239 + 0.2422 = 0.2661
P(–0.2238<X<0.4106) =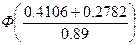 
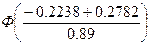– = Ф(0.77) – Ф(0.06) = 0.2794 – 0.0239 =
0.2555
P(X>0.4106) = 0.5 – 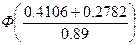= 0.5 – Ф(0.77)
= 0.5 – 0.2794 = 0.2206
Составим
расчетную таблицу для вычисления значения χ2.
|
W
|
P
|
W–P
|
(W–P)2
|
|
|
0.125
|
0.0869
|
0.0381
|
0.001452
|
0.016704
|
|
0.15625
|
0.1709
|
-0.01465
|
0.000215
|
0.001256
|
|
0.125
|
0.2661
|
-0.1411
|
0.019909
|
0.074819
|
|
0.34375
|
0.2555
|
0.08825
|
0.007788
|
0.030482
|
|
0.25
|
0.2206
|
0.0294
|
0.000864
|
0.003918
|
χ2набл = 32∙0.127 = 4.064
χ2теор = 43.77
Т.к. χ2набл< χ2теор,
то гипотеза о принятом теоретическом распределении не противоречит опытным
данным.