Задание 2.
Вариант 8.
Дано: Из
таблиц 2 и 3 получить 20 точек (xi,yi’)
и (xi,yi”)
i=1,
2, … 10, – значений двумерной случайной величины (X,Y).
Требуется:
1. Построить
линии регрессии Y на X и X на Y.
; 
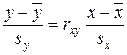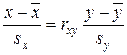
2. Проанализировать
полученные результаты
2.1. Сначала
наличие вероятностной зависимости между X и Y проверить с помощью неравенства 
. При этом зависимость фиксируется с уровнем значимости 0.05.
2.2. Если
наличие вероятностной зависимости зафиксировано, проверить адекватность
полученной линейной модели 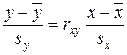или y=b0+b1x с
использованием критерия Фишера.
Исходные
данные.
|
№
|
X
|
Y’
|
Y”
|
|
1
|
51
|
78
|
85
|
|
2
|
59
|
82
|
95
|
|
3
|
66
|
86
|
105
|
|
4
|
70
|
86
|
90
|
|
5
|
82
|
94
|
105
|
|
6
|
93
|
117
|
125
|
|
7
|
105
|
117
|
129
|
|
8
|
114
|
123
|
129
|
|
9
|
121
|
142
|
156
|
|
10
|
129
|
160
|
178
|
Решение.
1. 
= (51∙2+
59∙2+ 66∙2+ 70∙2+ 82∙2+ 93∙2+ 105∙2+
114∙2+ 121∙2+ 129∙2)/20 = (102+ 118+ 132+ 140+ 164+ 186+ 210+
228+ 242+ 258)/20 = 1780/20 = 89
= (78+ 82+ 85+
86∙2+ 90+ 94+ 95+ 105∙2+ 117∙2+ 123+ 125+ 129∙2+ 142+
156+ 160+ 178)/20 = (78+ 82+ 85+ 172+ 90+ 94+ 95+ 210+ 234+ 123+ 125+ 258+ 142+
156+ 160+ 178)/20 = 2282/20 = 114.1
= (51∙78+ 51∙85+ 59∙82+ 59∙95+ 66∙86+ 66∙105+ 70∙86+ 70∙90+ 82∙94+ 82∙105+ 93∙117+ 93∙125+ 105∙117+ 105∙129+ 114∙123+ 114∙129+ 121∙142+ 121∙156+ 129∙160+ 129∙178)/20 = (3978+ 4335+ 4838+ 5605+ 5676+
6930+ 6020+ 6300+ 7708+ 8610+ 10881+ 11625+ 12285+ 13545+ 14022+ 14706+ 17182+ 18876+
20640+ 22962)/20 = 216724/20 = 10836.2
= (512∙2+ 592∙2+
662∙2+ 702∙2+ 822∙2+ 932∙2+
1052∙2+ 1142∙2+ 1212∙2+ 1292∙2)/20
= (5202+ 6962+ 8712+ 9800+ 13448+ 17298+ 22050+ 25992+ 29282+ 33282)/20 = 172028/20
= 8601.4
= (782+ 822+
852+ 862∙2+ 902+ 942+ 952+
1052∙2+ 1172∙2+ 1232+ 1252+
1292∙2+ 1422+ 1562+ 1602+ 1782)/20
= (6084+ 6724+ 7225+ 14792+ 8100+ 8836+ 9025+ 22050+ 27378+ 15129+ 15625+ 33282+
20164+ 24336+ 25600+ 31684)/20 = 276034/20 = 13801.7
= 8601.4-892
= 8601.4-7921 = 680.4
= 13801.7-114.12
= 13801.7-13018.81 = 782.89
Коэффициент
корреляции.
= 
= 
= 
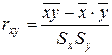= 0.9336
Уравнение
линейной регрессии Y по X.
Y-114.1=0.9336∙(27.98/26.08)∙(x-89)
Y-114.1=1∙(x-89)
Y-114.1=x-89
Y=x+25.1
Уравнение
линейной регрессии X по Y.
X-89=0.9336∙(26.08/27.98)∙(y-114.1)
X-89=0.87∙(y-114.1)
X-89=0.87y-0.87∙114.1
X-89=0.87y-99.267
X=0.87y-10.267
2. Наличие
вероятностной зависимости между X и Y
проверим с помощью неравенства .
Условие не
выполнено.
Для проверки
адекватности линейной модели нам необходимо найти значение критерия Фишера (F), который вычисляется по
формуле:
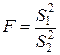, где S12 – Большая из дисперсий сравниваемых величин.
Мы сравниваем
значения дисперсий y и 
= x+25.1
S2(y) = 782.89 (см.
выше)
Значение
критерия Фишера равно
Критическое
значение критерия Фишера для вероятности 0.05 и 20 степеней свободы X и Y будет
равно 2.1242
Т.к.
эмпирическое значение меньше критического, то адекватность линейной модели
подтверждается.