Кафедра теории рынка.
Эконометрика.
X вариант 1. Y вариант 10.
Исходные данные.
|
X
|
Y
|
|
а
|
2.0
|
23.9
|
|
б
|
2.3
|
24.7
|
|
в
|
2.1
|
22.4
|
|
г
|
2.4
|
25.1
|
|
д
|
2.9
|
27.0
|
|
е
|
3.8
|
29.4
|
|
ж
|
3.3
|
34.2
|
|
з
|
4.6
|
30.6
|
|
и
|
5.1
|
35.2
|
|
к
|
5.4
|
34.0
|
1. Требуется нанести исходные данные на координатную
плоскость и сделать заключение о виде наблюдаемой зависимости.
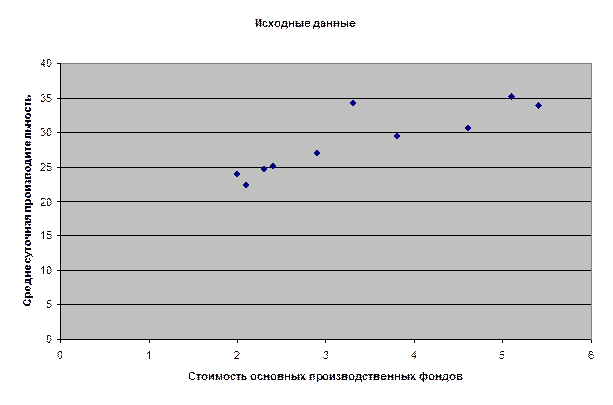
2. Рассчитать парные коэффициенты корреляции, по t–критерию Стьюдента
проверить его значимость и сделать соответствующий вывод.
Решение.
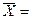 (2+2.1+2.3+2.4+2.9+3.3+3.8+4.6+5.1+5.4)/10 =
33.9/10 = 3.39
(2+2.1+2.3+2.4+2.9+3.3+3.8+4.6+5.1+5.4)/10 =
33.9/10 = 3.39
 (22.4+23.9+24.7+25.1+27+29.4+30.6+34+34.2+35.2)/10 = 286.5/10
= 28.65
(22.4+23.9+24.7+25.1+27+29.4+30.6+34+34.2+35.2)/10 = 286.5/10
= 28.65
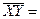 (2·23.9+2.1·22.4+2.3·24.7+2.4·25.1+2.9·27+3.3·34.2+3.8·29.4+4.6·30.6+5.1·35.2+5.4·34)/10
= (47.8+47.04+56.81+60.24+78.3+112.86+111.72+140.76+179.52+183.6)/10 =
(2·23.9+2.1·22.4+2.3·24.7+2.4·25.1+2.9·27+3.3·34.2+3.8·29.4+4.6·30.6+5.1·35.2+5.4·34)/10
= (47.8+47.04+56.81+60.24+78.3+112.86+111.72+140.76+179.52+183.6)/10 =
1018.65/10 =
101.86
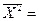 (22+2.12+2.32+2.42+2.92+3.32+3.82+4.62+5.12+5.42)/10 = (4+4.41+5.29+5.76+8.41+10.89+14.44+21.16+26.01+29.16)/10=
(22+2.12+2.32+2.42+2.92+3.32+3.82+4.62+5.12+5.42)/10 = (4+4.41+5.29+5.76+8.41+10.89+14.44+21.16+26.01+29.16)/10=
129.53/10=12.95
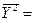 (22.42+23.92+24.72+25.12+272+29.42+30.62+342+34.22+35.22)/10
= (501.76+571.21+610.09+630.01+729+864.36+936.36+1156+1169.64+1239.04)/10=
(22.42+23.92+24.72+25.12+272+29.42+30.62+342+34.22+35.22)/10
= (501.76+571.21+610.09+630.01+729+864.36+936.36+1156+1169.64+1239.04)/10=
8407.47/10=840.75
Дисперсия X.
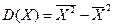 =
12.95-3.39^2=12.95-11.4921=1.4579
=
12.95-3.39^2=12.95-11.4921=1.4579
Среднеквадратическое отклонение X.
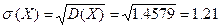
Дисперсия Y.
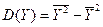 =
840.75-28.65^2=840.75-820.8225=19.9275
=
840.75-28.65^2=840.75-820.8225=19.9275
Среднеквадратическое отклонение Y.
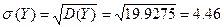
Коэффициент корреляции.
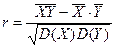 =
= 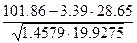 =
= 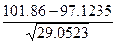 =
= 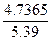 = 0.8788
= 0.8788
Значимость коэффициента корреляции проверим следующим
образом: если 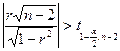 , то гипотеза о
существенном отличии коэффициента r от нуля принимается, а в противном случае
– отвергается.
, то гипотеза о
существенном отличии коэффициента r от нуля принимается, а в противном случае
– отвергается.
Найдем значение левой части неравенства.
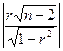 =
= 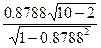 =
= 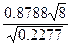 =
= 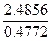 = 5.2
= 5.2
По таблице распределения Стьюдента найдем, что для 10
значений этот коэффициент соответствует уровню значимости более, чем 99.95%.
Следовательно, гипотеза подтверждается.
3. Записать уравнение парной регрессии и объяснить смысл
каждой составляющей.
Решение.
Уравнение линейной регрессии Y по X.
Y-28.65=0.8788·(4.46/1.21)·(x-3.39)
Y-28.65=3.24·(x-3.39)
Y-28.65=3.24·x-3.24·3.39
Y-28.65=3.24·x-10.98
Y=3.24·x+17.67
Это означает, что при увеличении x на 1, y увеличится
на 3.24.
Уравнение линейной регрессии X по Y.
X-3.39=0.8788·(1.21/4.46)·(y-28.65)
X-3.39=0.24·(y-28.65)
X-3.39=0.24·y-0.24·28.65
X-3.39=0.24·y-6.88
X=0.24·y–3.49
Это означает, что при увеличении y на 1, x увеличится
на 0.24.
4. В соответствии с методом наименьших квадратов составить
систему нормальных уравнений и любым способом решить ее. Дать интерпретацию
полученным результатам.
Решение.
Обозначим a=(a0,a1) – решение
системы нормальных уравнений,
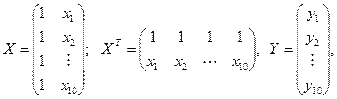
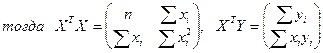
В данных обозначениях система нормальных уравнений будет
выглядеть следующим образом: (XTX)a=XTY , и, соответственно
вектор а можно будет найти по формуле: a=(XTX)-1(XTY).
Подставив значения, получим:
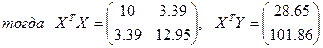
определитель матрицы XTX равен 118.008
Обратная матрица
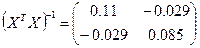
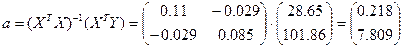
Получили нормальное уравнение метода наименьших квадратов Y=0.218+7.809X
Полученные результаты можно трактовать следующим образом:
увеличение стоимости основных фондов на 1 млн. руб. приводим к росту
среднесуточной производительности на 7.809 тонн. Коэффициент a0=0.218 теоретически
обозначает среднесуточную производительность при нулевой стоимости основных
фондов, но это именно теоретическое предположение.
5. По t–критерию
Стьюдента проверить значимость всех параметров построенного регрессионного
уравнения. Для значимых параметров найти доверительные интервалы.
Решение.
Найдем доверительный интервал для коэффициентов уравнения Y=3.24·x+17.67
Доверительный интервал для коэффициента а0
(свободного члена) рассчитывается по формуле:
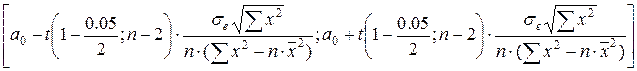
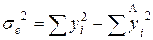
 =
= 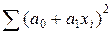 =
= 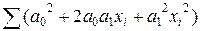 =
= 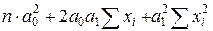 = 10∙17.672+2∙17.67∙3.24∙33.9+3.242∙12.95
= 7139.83
= 10∙17.672+2∙17.67∙3.24∙33.9+3.242∙12.95
= 7139.83
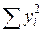 = 8407.47
= 8407.47
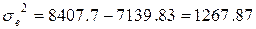
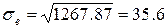
Получаем следующий доверительный интервал:
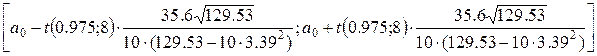
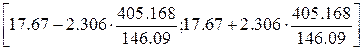
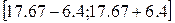
[11.27;24.07]
Доверительный интервал для коэффициента a1 (при x) рассчитывается по формуле:
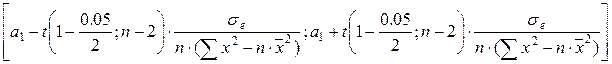
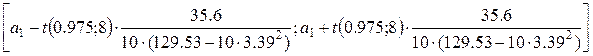
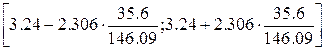
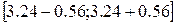
[2.68;3.8]
Найдем доверительный интервал для коэффициентов уравнения X=0.24·y–3.49
Доверительный интервал для коэффициента а0
(свободного члена) рассчитывается по формуле:
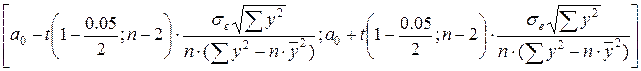
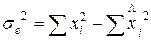
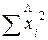 =
= 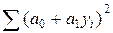 =
= 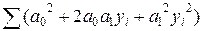 =
= 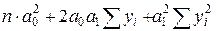 = 10∙3.492+2∙(-3.49)∙0.24∙286.5+0.242∙8407.47 = 126.13
= 10∙3.492+2∙(-3.49)∙0.24∙286.5+0.242∙8407.47 = 126.13
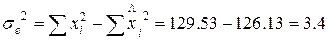
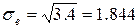
Получаем следующий доверительный интервал:
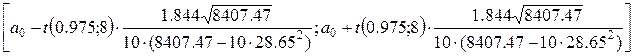
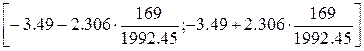
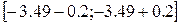
[–3.69;–3.29]
Доверительный интервал для коэффициента a1 (при y) рассчитывается по формуле:
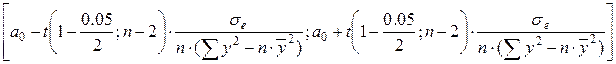
Получаем следующий доверительный интервал:
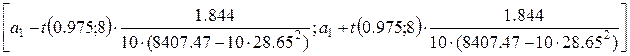
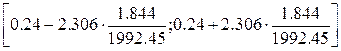
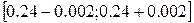
[0.238;0.242]
6. Провести разложение общей суммы квадратов. Вычислить
коэффициент детерминации и дать интерпретацию полученным результатам.
Решение.
Коэффициент детерминации.
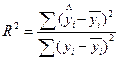 , где
, где 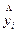 – значение y, вычисленное через уравнение
регрессии.
– значение y, вычисленное через уравнение
регрессии.
Подставив значения, получим:
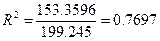
Высокое значение коэффициента детерминации (>0.5) говорит
о тесной связи между исследуемыми величинами.
7. По F–критерию
Фишера проверить значимость всего регрессионного уравнения в целом.
Решение.
Значение критериальной статистики F рассчитывается
по формуле:
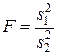 , где si2–
выборочные оценки дисперсий (i = 1, 2), а s12 – наибольшая
по величине дисперсия. Эти значения дисперсий вычислены в предыдущем пункте.
, где si2–
выборочные оценки дисперсий (i = 1, 2), а s12 – наибольшая
по величине дисперсия. Эти значения дисперсий вычислены в предыдущем пункте.
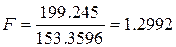
Теоретическое значение критерия F0.1;10;10 = 2.3226
Т.к. Fрасчетное<Fтеоретическое, то
гипотеза значимости подтверждается.
8. Построить таблицу дисперсионного анализа.
9. Выбрать точку Xn вдали от основного массива
данных и для нее вычислить точечный прогноз значения зависимой переменной.
Решение.
Возьмем Xn=10.
По уравнению регрессии получим Y(10)=3.24·10+17.67=32.4+17.67=50.07
10. Построить доверительный интервал для регрессионного
уравнения в целом.
Решение.
Доверительные интервалы для уравнения парной регрессии y=a0+a1x находятся по
формуле:
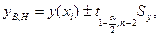 где yв, yн – соответственно верхняя и
нижняя границы доверительного интервала; xi – значение независимой переменной, для которой
определяется доверительный интервал.
где yв, yн – соответственно верхняя и
нижняя границы доверительного интервала; xi – значение независимой переменной, для которой
определяется доверительный интервал.
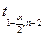 – квантиль
распределения Стьюдента (1–α) – доверительная вероятность, (n–2) – число степеней
свободы.
– квантиль
распределения Стьюдента (1–α) – доверительная вероятность, (n–2) – число степеней
свободы.
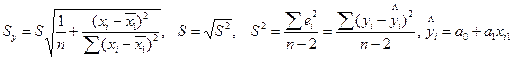
Пусть 1–α=0.9, тогда t0.95,10 = 1.812
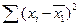 = 14.609
= 14.609
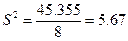
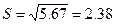
Найдем границы доверительного интервала для x=xmin=2
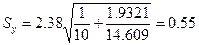
y(2) = 3.24·2+17.67 = 6.48+17.67 = 24.15

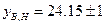
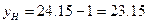
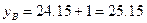
Найдем границы доверительного интервала для x=xmax=5.4
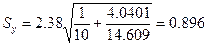
y(5.4)
= 3.24·5.4+17.67 = 17.496+17.67 = 35.166
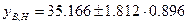
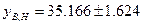
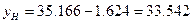
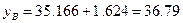
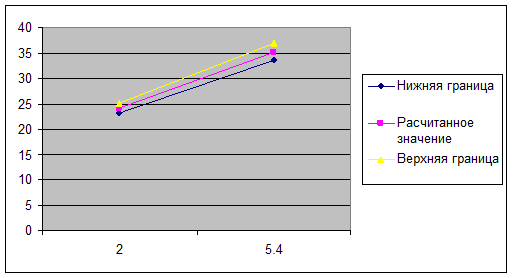
11. В одной системе координат изобразить исходные данные,
построенные регрессионные уравнения и найденный доверительный интервал.
12. Сделать общий вывод по всем полученным результатам.
Решение.
Регрессионная связь между указанными величинами высокая, ее
можно описать уравнениями:
Y=3.24·x+17.67
X=0.24·y–3.49
Литература.
1. Магнус Я.А., Катышев П.К., Пересецкая А.А, Эконометрика.
Начальный курс. Москва. 1997г. – 248с.
2. Елисеева И.И. Эконометрика. М. 2001 – 344с.
3. Айвозен С.А., Мхиторян В.С. Прикладная статистика и
основы эконометрики. М. 1998 – 1022с.
4. Доугерти К. Введение в эконометрику. М. 1999 – 402 с.