Контрольная работа № 1.
Задача 4. Даны
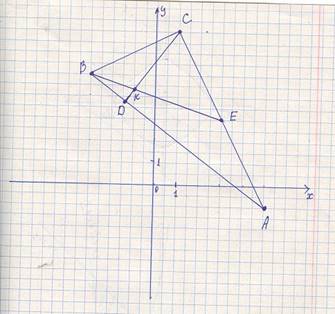
вершины A(5;–1), B(–3;5), C(1;7) треугольника. Сделать чертеж и
найти:
1) длину
стороны AB;
2) внутренний
угол A в радианах с
точностью до 0.01;
3) уравнение
высоты, проходящей через вершину С;
4) уравнение
медианы, проведенной через вершину B;
5) точку
пересечения медианы BE и высоты CD;
6) длину
высоты, проведенной через вершину C.
Решение.
1) Длина
стороны AB.
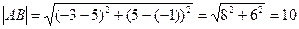
2) внутренний
угол A в радианах с
точностью до 0.01;
= 
= 
= 
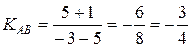
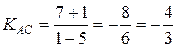
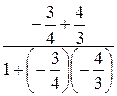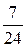
3) уравнение
высоты, проходящей через вершину С;
D –
точка пересечения высоты, проведенной через вершину С и стороны AB.
Уравнение
высоты CD.
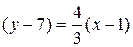
3y–21=4x–4
4x–3y+17=0
4) уравнение
медианы, проведенной через вершину B;
Середина
стороны AC – точка E(3;3).
Уравнение
медианы BE.
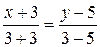
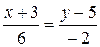
–2x–6=6y–30
2x+6y–24=0
x+3y–12=0
5) точку
пересечения медианы BE и высоты CD;
Найдем
координаты точки K – пересечения
высоты CD и медианы BE.
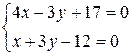
5x+5=0
x=–1
–1+3y–12=0
3y=13
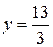
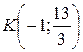
6) длину
высоты, проведенной через вершину C.
Уравнение
высоты CD.
4x–3y+17=0
Уравнение
стороны AB.
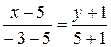
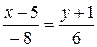
6x–30=–8y–8
6x+8y–22=0
3x+4y–11=0
Найдем
координаты точки D – пересечения
высоты CD и стороны AB.
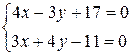
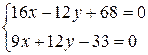
25x+35=0
x=–1.4
–4.2+4y–11=0
4y=15.2
y=3.8
D(–1.4;3.8)
Длина высоты CD.
= 
= 
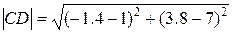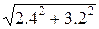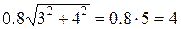
Задача 14. Найти
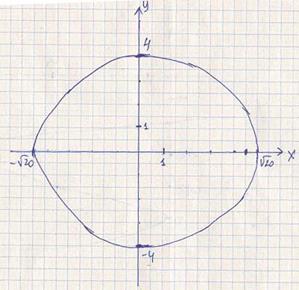
уравнение линии как геометрического места точек и построить эту линию. Составить
уравнение геометрического места точек, отношение расстояний которых до точки F(–2;0) и до прямой X=–10 равно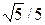 
.
Решение.
Расстояние от
точки с координатами (x;y) до точки F с координатами
(–2;0) будет равно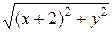 
Расстояние от
точки с координатами (x;y) до прямой x=–10 равно x+10.
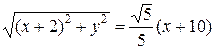
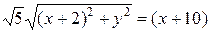
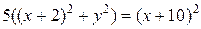
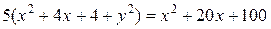
4x2+5y2=80
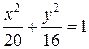
Эллипс.
Задача 32.
Найти производные заданных функций.
а)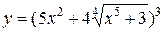 
= 
= 
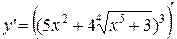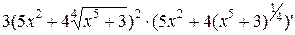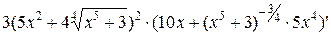
в)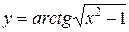 
= 
= 
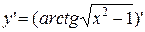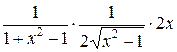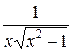
47.
Исследовать средствами дифференциального исчисления функцию y=x3–14x2+60x–72 и построить ее график.
Решение.
y(0)=–72
x3–14x2+60x–72=(x–6)2(x–2)
Область
определения функции – вся числовая прямая.
f(x)≠±f(x) – функция не является ни четной, ни нечетной.
Функция не
является периодической. Функция непрерывна во всей области определения. Найдем
поведение функции на концах области определения.
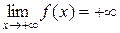
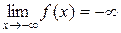
Исследуем
функцию по производной.
y'=3x2–28x+60
3x2–28x+60=0
|
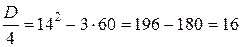
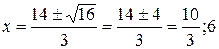
x
|
|
|
|
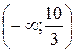
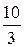
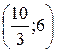
6
|
|
|
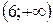
y'
|
+
|
0
|
–
|
0
|
+
|
|
y
|
↑
|
max
|
↓
|
min
|
↑
|
= 
= 
= 
= 
= 
= 
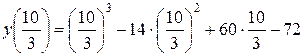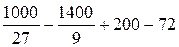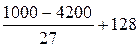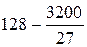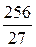y(6)=63–14∙62+60∙6–72=216–504+360–72=0
Исследуем
функцию по второй производной.
y"=6x–28
6x–28=0
|
x
|
|
|
|
|
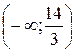
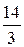
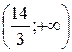
y”
|
–
|
0
|
+
|
|
y
|
выпукла
|
т. перегиба
|
вогнута
|
= 
= 
= 
= 
= 
= 
= 
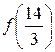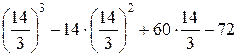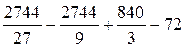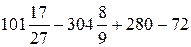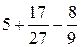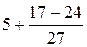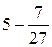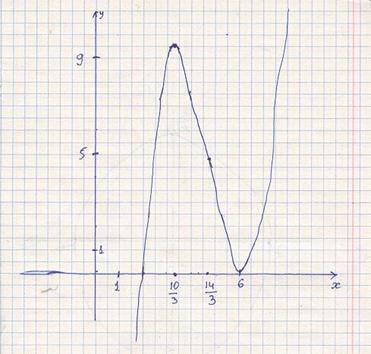
Контрольная работа №
2.
Задача 10. Найти
неопределенные интегралы. Результат проверить дифференцированием.
а)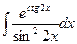 
=
=
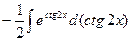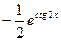+С
Проверка.
=
=
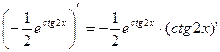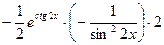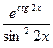
б)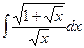 
=
=
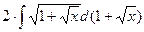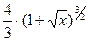+С
Проверка.
=
=
=
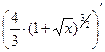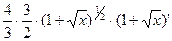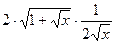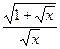
в)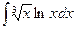 
= 
= 
= 
= 
=
=
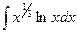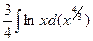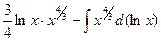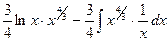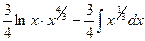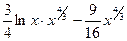+С
Проверка.
=
=
= 
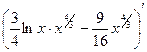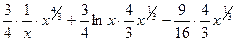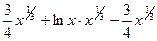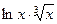
г)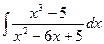 
Преобразуем
подынтегральное выражение.
x3–5=(x2–6x+5)(x+6)+(31x–35)
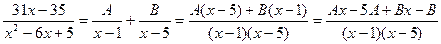
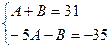
Сложив
уравнения, получим
–4A=–4
A=1
1+B=31
B=30
Получается
Учитывая все
вышеизложенное, получаем:
=
=
=
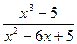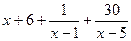
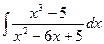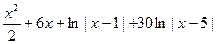+С
Проверка.
= = 
= 
= 
= 
=.
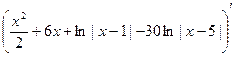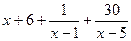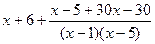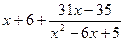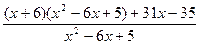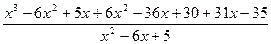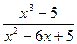Задача 12. Вычислить
площадь фигуры, ограниченной параболой y=x2–6x+7 и прямой y=x+1. Сделать чертеж.
Решение.
Найдем точки
пересечения графиков.
x2–6x+7=x+1
x2–7x+6=0
D=49–24=25
x=1; x=6.
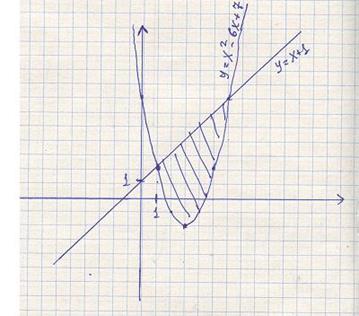
Площадь
фигуры, ограниченной указанными линиями равна:
= 
= 
= 
= 
= 
= 
= 
= 
= 
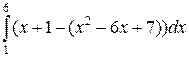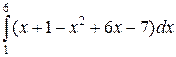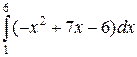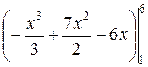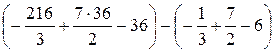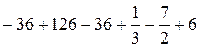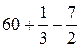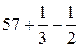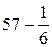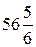
Задача 21. Найти
общее решение дифференциального уравнения (x2+1)y’–xy=x(x2+1) и частное решение, удовлетворяющее начальному
условию y=6 при x=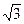
.
Решение
(x2+1)y’–xy=x(x2+1)
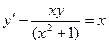
Найдем решение
однородного уравнения.
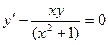
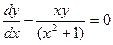
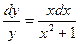
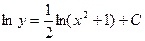
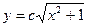
Решение
исходного уравнения найдем методом вариации постоянной.
C=C(x)
=
=
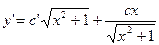
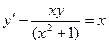
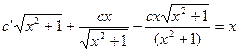
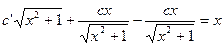
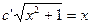
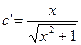
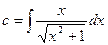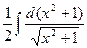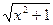+C1
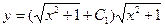
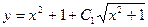
Это общее
решение дифференциального уравнения.
Найдем частное
решение, удовлетворяющее начальным условиям.
y(x0)=y0
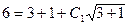
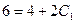
2C1=2
C1=1
Получаем
частное решение
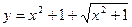
Задача 37. Найти
частные производные и полный дифференциал функции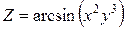 
Решение.
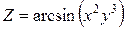
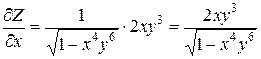
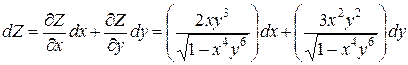
Задачи 48.
Дана функция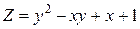 
и точка M(2;1).
Найти: а)
градиент функции Z в точке M(2;1);
б) производную
функции Z в точке M
по направлению вектора: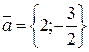 
.
Решение.
Найдем частные
производные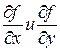 
.
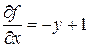
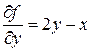
Градиент
функции Z
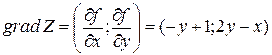
Градиент
функции Z в точке M(2;1)
(–1+1;2-2)=(0;0)
Так как
градиент функции в данной точке равен нулевому вектору, то производная по
любому направлению в этой точке будет равна 0.