Вариант 4
Задача 4.1.
Проведены измерения уровня интеллектуального развития (IQ) десяти американских семей. С помощью
коэффициентов ранговой корреляции определите, согласуются ли значения
коэффициентов IQ у
родителей и их детей.
|
Семья
|
Значения IQ
|
|
Для родителей
|
Для детей
|
|
1
|
125
|
110
|
|
2
|
120
|
105
|
|
3
|
110
|
95
|
|
4
|
105
|
125
|
|
5
|
105
|
120
|
|
6
|
95
|
105
|
|
7
|
95
|
75
|
|
8
|
90
|
95
|
|
9
|
80
|
90
|
|
10
|
75
|
80
|
Решение.
Коэффициент ранговой корреляции Спирмена рассчитывается по формуле:
.
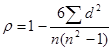Коэффициент ранговой корреляции Кендэлла рассчитывается по формуле:
.
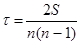Составляем расчетную таблицу:
|
Семья
|
Значения IQ
|
Разность рангов
d
|
d2
|
Баллы для рангов
|
|
Для родителей
R1
|
Для детей
R2
|
Положи-
тельные
Q
|
Отрица-тельные
Р
|
Итого
|
|
10
|
1
|
2
|
-1
|
1
|
8
|
1
|
7
|
|
9
|
2
|
3
|
-1
|
1
|
7
|
1
|
6
|
|
8
|
3
|
4,5
|
-1,5
|
2,25
|
5
|
1
|
4
|
|
6
|
4,5
|
6,5
|
-2
|
4
|
3
|
2
|
1
|
|
7
|
4,5
|
1
|
3,5
|
12,25
|
5
|
0
|
5
|
|
4
|
6,5
|
10
|
-3,5
|
12,25
|
0
|
4
|
-4
|
|
5
|
6,5
|
9
|
-2,5
|
6,25
|
0
|
3
|
-3
|
|
3
|
8
|
4,5
|
3,5
|
12,25
|
2
|
0
|
2
|
|
2
|
9
|
6,5
|
2,5
|
6,25
|
1
|
0
|
1
|
|
1
|
10
|
8
|
2
|
4
|
0
|
0
|
0
|
|
Итого
|
|
|
|
61,5
|
|
|
19
|
Получаем:
.
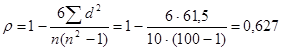
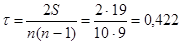Вывод:
Так как коэффициенты ранговой корреляции не близки к нулю и не близки к
1, то согласованность значений
коэффициентов IQ у
родителей и их детей средняя.
Задача 4.2.
Является ли данное распределение – распределением Пуассона?
|
Количество бракованных из-
делий на 100 проверок
|
Число рабочих
|
|
0
|
282
|
|
1
|
160
|
|
2
|
39
|
|
3
|
15
|
|
4
|
3
|
|
5
|
1
|
|
Итого
|
500
|
Решение.
Проверяем примерное равенство средней и дисперсии. Составляем расчетную
таблицу:
|
x
|
f
|
x*f
|
|
|
|
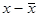
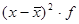
0
|
282
|
0
|
-0,6
|
101,52
|
|
1
|
160
|
160
|
0,4
|
25,6
|
|
2
|
39
|
78
|
1,4
|
76,44
|
|
3
|
15
|
45
|
2,4
|
86,4
|
|
4
|
3
|
12
|
3,4
|
34,68
|
|
5
|
1
|
5
|
4,4
|
19,36
|
|
Итого
|
500
|
300
|
11,4
|
344
|
|
Итого/500
|
|
0,6
|
0,0228
|
0,688
|
Получаем:
, 
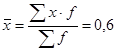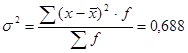. Итак, 
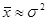, следовательно, данное распределение может быть
распределением Пуассона.
Рассчитаем
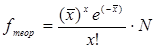и 
:
|
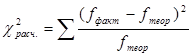Количество бракованных из-
делий на 100 проверок
|
Число рабочих
|
|
|
|
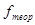
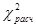
0
|
282
|
274,406
|
0,210
|
|
1
|
160
|
164,643
|
0,131
|
|
2
|
39
|
49,393
|
2,187
|
|
3
|
15
|
9,879
|
2,655
|
|
4
|
3
|
1,482
|
1,556
|
|
5
|
1
|
0,178
|
3,802
|
|
Итого
|
500
|
500
|
10,540
|
, 
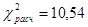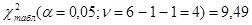
Так как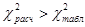 
, то распределение не является распределением Пуассона.
Задача 4.3.
Имеются данные о количестве совершенных преступлений против
собственности:
|
Активность
полиции
|
Среднедушевой доход в районе
|
Итого
|
|
Низкий
|
Средний
|
Высокий
|
|
Низкая
|
115
|
128
|
100
|
343
|
|
Умеренная
|
98
|
100
|
80
|
278
|
|
Высокая
|
90
|
50
|
30
|
170
|
|
Всего
|
303
|
278
|
210
|
791
|
Оцените уровень связи признаков с помощью коэффициентов взаимной
сопряженности и теоретико-информационных мер связи.
Решение.
Проверяем условие: 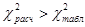, где
.
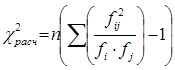Получаем: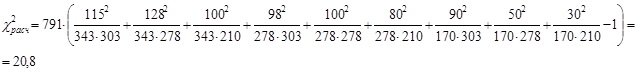 
.
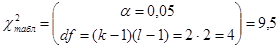Так
как 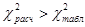, то среднедушевой доход в районе можно считать фактором
количества совершенных преступлений против собственности.
Коэффициент взаимной сопряженности Пирсона:
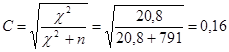
Коэффициент взаимной сопряженности
Чупрова:
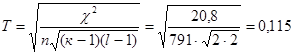
Скорректированный коэффициент Пирсона:
, 
, 
.
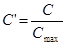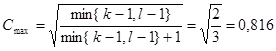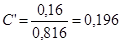Таким образом, между среднедушевым доход в районе и
количеством совершенных преступлений против собственности существует не очень
тесная связь.
Задача 4.4.
Заполните пустующие ячейки таблицы сопряженности. Есть ли взаимосвязь
между признаками? Если «да», охарактеризуйте ее тесноту с помощью известных
показателей.
|
Средний возраст
родителей при
рождении
ребенка
|
Успеваемость ребенка в школе
|
Итого
|
|
Неуд.
|
Удовл.
|
Хорошо
|
Отлично
|
|
16-20
|
|
45
|
38
|
12
|
110
|
|
21-25
|
10
|
|
56
|
18
|
|
|
26-30
|
3
|
26
|
40
|
|
107
|
|
31-35
|
6
|
25
|
45
|
|
106
|
|
36-40
|
10
|
40
|
|
27
|
115
|
|
41-45
|
8
|
38
|
40
|
30
|
|
|
Всего
|
|
216
|
|
|
|
Решение.
Заполним
пустые ячейки:
|
Средний возраст
родителей при
рождении
ребенка
|
Успеваемость ребенка в школе
|
Итого
|
|
Неуд.
|
Удовл.
|
Хорошо
|
Отлично
|
|
16-20
|
15
|
45
|
38
|
12
|
110
|
|
21-25
|
10
|
42
|
56
|
18
|
126
|
|
26-30
|
3
|
26
|
40
|
38
|
107
|
|
31-35
|
6
|
25
|
45
|
30
|
106
|
|
36-40
|
10
|
40
|
38
|
27
|
115
|
|
41-45
|
8
|
38
|
40
|
30
|
116
|
|
Всего
|
52
|
216
|
257
|
155
|
680
|
Проверяем условие: 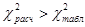, где
.
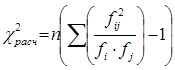Получаем: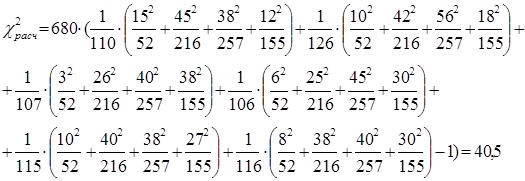 
.
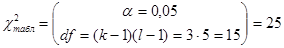Так как 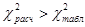, то средний возраст родителей при рождении ребенка можно
считать фактором успеваемости ребенка в школе.
Охарактеризуем тесноту взаимосвязи
с помощью коэффициентов взаимной сопряженности.
Коэффициент взаимной сопряженности Пирсона:
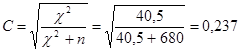
Коэффициент взаимной сопряженности
Чупрова:
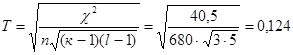
Скорректированный коэффициент Пирсона:
, 
, 
.
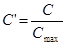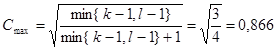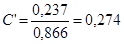Таким
образом, между средним возрастом родителей при рождении ребенка и успеваемостью
ребенка в школе существует заметная связь.