Содержание
Задача № 1. 3
Задача № 2. 6
Задача № 1
УСЛОВИЕ ЗАДАЧИ:
Транспортная задача
Имеются данные о поставщиках
пиломатериалов, расположенные в пунктах А1, А2 и А3 с мощностью производства
55, 18, 91 тыс. руб. Имеются потребители этого продукта В1, В2, В3, В4, В5 с
объемами спроса 26, 47, 54, 37 и 26 тыс. руб. Известны транспортные расходы на
перевозку единицы груза от каждого поставщика к каждому потребителю,
представленные матрицей тарифов
13 14 12 9 11
8 9 6 4 7
10 8 7 7 8
Требуется найти план перевозок грузов от
поставщиков к потребителям, при котором транспортные расходы будут минимальными
РЕШЕНИЕ:
1) Построим экономико-математическую модель задачи.
|
13
|
14
|
12
|
9
|
11
|
55
|
|
8
|
9
|
6
|
4
|
7
|
18
|
|
10
|
8
|
7
|
7
|
8
|
91
|
|
26
|
47
|
54
|
37
|
26
|
|
∑ аi = 165
∑bj = 190
xij – искомый объем перевозки от поставщика к
потребителю (поставка клетки)
Чтобы
мощность каждого поставщика была реализована, надо составить уравнение баланса для каждой строки:
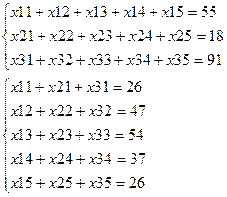
Очевидно,
что объем перевозимого груза не может быть отрицательным, поэтому следует
дополнительно предположить, что:
xij ≥ 0,
Тогда,
суммарные затраты на перевозку выражаются через коэффициент затрат и поставки
следующим образом:
F=13х11+14х12+12х13+9х14+11х15+8х21+9х22+6х23+4х24+7х25+10х31+8х32+7х33+7х34+8х35→min
2) Решим задачу методом наименьших затрат
Находим в таблице поставок клетки с наименьшим коэффициентом затрат.
Такая клетка одна (2,3) с коэффициентом затрат равным 6. сравним максимально возможные поставки для нее: х23 =
min (54, 18) = 18. в результате мощность
второго поставщика полностью исчерпана, поэтому оставшиеся клетки для второго поставщика перечеркиваем
пунктирной линией.
В оставшейся таблице наименьшим коэффициентом затрат обладают две
клетки (3,4) и (3,5). Сравним максимально возможные поставки для этих клеток: х
34 =min (37, 91) = 37 и х35 = min (26;91)= 26. Даем поставку в клетку
(3,4), для которой максимально возможная поставка оказалась больше. В итоге из рассмотрения выпадает столбец 4.
Далее действуем по той же схеме. В итоге получаем следующее:
|
|
26
|
47
|
54
|
37
|
26
|
|
 55 55
|
13
|
 14 14
|
  12 12
|
 9 9
|
11
|
|
|
26
|
3
|
|
|
26
|
|
 18 18
|
 8 8
|
9
|
  6 6
|
 4 4
|
7
|
|
|
|
|
18
|
|
|
|
91
|
  10 10
|
8
|
 7 7
|
  7 7
|
8
|
|
|
|
18
|
36
|
37
|
|
|
26
|
 
|
|

|
 
|
|
|
|
|
26
|
|
|
|
Был
добавлен фиктивный поставщик с мощностью 26 единиц.
Таким образом,
вычислим суммарные минимальные затраты в денежных единицах:
F = 13*26 + 14*3
+8*18 + 6* 18 + 7*36 + 7*37 +11*26 = 1429
(ед.)
Тогда план перевозок грузов от поставщиков к
потребителям при минимальных затратах будет выглядеть так:
Или:
 26 3 0 0 26
26 3 0 0 26
0 0 18 0 0
0 18 36 37 0
Задача № 2
УСЛОВИЕ ЗАДАЧИ:
Трендовая модель
Имеются данные (условные) о потреблении дизельного топлива
за 1998- 2003 годы по одному из крупных регионов, которые приведены в таблице
1. На основе имеющихся данных требуется решить следующие задачи:
1) Построить ломаную кривую изменения потребления дизельного топлива во времени.
Выдвинуть гипотезу о виде зависимости объема потребления дизельного топлива от
времени. Оценить неизвестные параметры методом наименьших квадратов
2) Для найденного уравнения регрессии построить
доверительную полосу при уровне доверия 0,9. Нарисовать ее на графике вместе с
линией регрессии
3) По линейному уравнению тренда найти точечный и
интервальный прогноз среднего потребления дизельного топлива в 2007 году и 2009 году
(доверительную вероятность принять равной 0,9). Изобразить на графике точечный
и интервальный прогноз.
РЕШЕНИЕ:
Таблица 1
Исходные данные
|
Год
|
Объем
потребления, тыс руб.
|
|
1988
|
1
|
|
1989
|
0,8
|
|
1990
|
0,8
|
|
1991
|
0,9
|
|
1992
|
1,1
|
|
1993
|
1,2
|
|
1994
|
1,4
|
|
1995
|
1,3
|
|
1996
|
1,5
|
|
1997
|
1,7
|
|
1998
|
1,6
|
|
1999
|
1,2
|
|
2000
|
1,7
|
|
2001
|
1,9
|
|
2002
|
1,8
|
|
2003
|
1,7
|
Рис. 1. Зависимость объемов потребления
дизельного топлива от года, тыс. руб.
Найдем параметры уравнения регрессии
методом наименьших квадратов.
Предполагается наличие линейной связи между Х и У, то есть регрессионная
модель описывается функцией:
Уi’ = а0 + а1 х, (1)
где Уi’ – значение результативного признака;
а0 и а1 – параметры уравнения
регрессии, определяемые из системы уравнений:
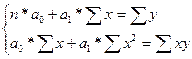 , (2)
, (2)
Для
нахождения параметров уравнения регрессии по методу наименьших квадратов,
составим расчетную таблицу (таблица 2)
Таблица 2
Расчетная таблица для нахождения параметров
уравнения регрессии
|
№ п/п
|
Х
|
У
|
Х2
|
ХУ
|
У'
|
Уi - У'
|
/Уi - У'//Уi
|
|
1
|
1988
|
1
|
3952144
|
1988
|
538,11
|
-537,11
|
537,11
|
|
2
|
1989
|
0,8
|
3956121
|
1591,2
|
538,38
|
-537,58
|
671,975
|
|
3
|
1990
|
0,8
|
3960100
|
1592
|
538,65
|
-537,85
|
672,3125
|
|
4
|
1991
|
0,9
|
3964081
|
1791,9
|
538,92
|
-538,02
|
597,8
|
|
5
|
1992
|
1,1
|
3968064
|
2191,2
|
539,19
|
-538,09
|
489,1727
|
|
6
|
1993
|
1,2
|
3972049
|
2391,6
|
539,46
|
-538,26
|
448,55
|
|
7
|
1994
|
1,4
|
3976036
|
2791,6
|
539,73
|
-538,33
|
384,5214
|
|
8
|
1995
|
1,3
|
3980025
|
2593,5
|
540
|
-538,7
|
414,3846
|
|
9
|
1996
|
1,5
|
3984016
|
2994
|
540,27
|
-538,77
|
359,18
|
|
10
|
1997
|
1,7
|
3988009
|
3394,9
|
540,54
|
-538,84
|
316,9647
|
|
11
|
1998
|
1,6
|
3992004
|
3196,8
|
540,81
|
-539,21
|
337,0063
|
|
12
|
1999
|
1,2
|
3996001
|
2398,8
|
541,08
|
-539,88
|
449,9
|
|
13
|
2000
|
1,7
|
4000000
|
3400
|
541,35
|
-539,65
|
317,4412
|
|
14
|
2001
|
1,9
|
4004001
|
3801,9
|
541,62
|
-539,72
|
284,0632
|
|
15
|
2002
|
1,8
|
4008004
|
3603,6
|
541,89
|
-540,09
|
300,05
|
|
16
|
2003
|
1,7
|
4012009
|
3405,1
|
542,16
|
-540,46
|
317,9176
|
|
ИТОГО
|
31928
|
21,6
|
63712664
|
43126,1
|
8642,16
|
-8620,56
|
6898,349
|
Подставляем
полученные значения из таблицы 2 в формулу (2):
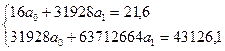
Из
первого уравнения выражаем а0, подставляем во второе уравнение и
получаем соответствующее значение:
а1 = 0,07 и а0 = 138,3
Тогда
искомое уравнение регрессии имеет вид:
Уi’=
138.3 + 0,07Х.
1) Для проверки адекватности определим среднее относительное
линейное отклонение по формуле (7)
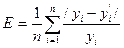 , (3)
, (3)
Подставляя
значения из таблицы 2 в формулу (3), получим:
Е = 0,10 или 10 %.
Так
как Е меньше 15 %, то связь между факторным и результативным признаками
достаточно тесная.
Полученное
уравнение регрессии пригодно для прогнозных значений, так как значение Е меньше
15 %.
2) Для построения доверительной полосы найдем у’(t) для каждого значения t с
использованием уравнения регрессии и таблицы 3
Таблица 3
|
t
|
Х
|
У(Х)
|
У'(t)
|
У'(Х)
|
|
1
|
1988
|
1
|
138,73
|
0,36
|
|
2
|
1989
|
0,8
|
138,66
|
0,43
|
|
3
|
1990
|
0,8
|
138,59
|
0,5
|
|
4
|
1991
|
0,9
|
138,52
|
0,57
|
|
5
|
1992
|
1,1
|
138,45
|
0,64
|
|
6
|
1993
|
1,2
|
138,38
|
0,71
|
|
7
|
1994
|
1,4
|
138,31
|
0,78
|
|
8
|
1995
|
1,3
|
138,24
|
0,85
|
|
9
|
1996
|
1,5
|
138,17
|
0,92
|
|
10
|
1997
|
1,7
|
138,1
|
0,99
|
|
11
|
1998
|
1,6
|
138,03
|
1,06
|
|
12
|
1999
|
1,2
|
137,96
|
1,13
|
|
13
|
2000
|
1,7
|
137,89
|
1,2
|
|
14
|
2001
|
1,9
|
137,82
|
1,27
|
|
15
|
2002
|
1,8
|
137,75
|
1,34
|
|
16
|
2003
|
1,7
|
137,68
|
1,41
|
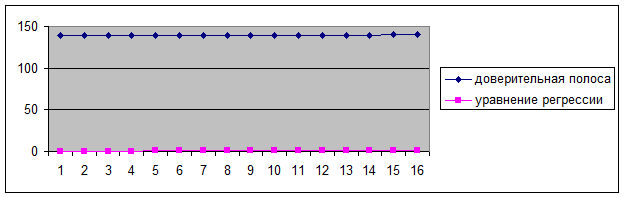
Рис.
2. Уравнение регрессии и доверительная
полоса
3) Оценим условное математическое ожидание для 2007 года Мt = 20
Оценкой 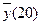 является групповая
средняя у’(t= 20)= 138,8 + 0,07
*20= 137,4
является групповая
средняя у’(t= 20)= 138,8 + 0,07
*20= 137,4
Найдем
оценку S 2
дисперсии δ2. Используем данные таблицы 4
Таблица 4
|
t
|
Х
|
У'(t = 20)
|
У'(t )
|
еt
|
еt-1
|
еt*еt
|
t - tср
|
(t - tср)2
|
|
1
|
1988
|
138,94
|
138,87
|
-0,07
|
-
|
0,0049
|
-7,5
|
56,25
|
|
2
|
1989
|
138,94
|
138,94
|
0
|
-0,07
|
0
|
-6,5
|
42,25
|
|
3
|
1990
|
138,94
|
139,01
|
0,07
|
0
|
0,0049
|
-5,5
|
30,25
|
|
4
|
1991
|
138,94
|
139,08
|
0,14
|
0,07
|
0,0196
|
-4,5
|
20,25
|
|
5
|
1992
|
138,94
|
139,15
|
0,21
|
0,14
|
0,0441
|
-3,5
|
12,25
|
|
6
|
1993
|
138,94
|
139,22
|
0,28
|
0,21
|
0,0784
|
-2,5
|
6,25
|
|
7
|
1994
|
138,94
|
139,29
|
0,35
|
0,28
|
0,1225
|
-1,5
|
2,25
|
|
8
|
1995
|
138,94
|
139,36
|
0,42
|
0,35
|
0,1764
|
-0,5
|
0,25
|
|
9
|
1996
|
138,94
|
139,43
|
0,49
|
0,42
|
0,2401
|
0,5
|
0,25
|
|
10
|
1997
|
138,94
|
139,5
|
0,56
|
0,49
|
0,3136
|
1,5
|
2,25
|
|
11
|
1998
|
138,94
|
139,57
|
0,63
|
0,56
|
0,3969
|
2,5
|
6,25
|
|
12
|
1999
|
138,94
|
139,64
|
0,7
|
0,63
|
0,49
|
3,5
|
12,25
|
|
13
|
2000
|
138,94
|
139,71
|
0,77
|
0,7
|
0,5929
|
4,5
|
20,25
|
|
14
|
2001
|
138,94
|
139,78
|
0,84
|
0,77
|
0,7056
|
5,5
|
30,25
|
|
15
|
2002
|
138,94
|
139,85
|
0,91
|
0,84
|
0,8281
|
6,5
|
42,25
|
|
16
|
2003
|
138,94
|
139,92
|
0,98
|
0,91
|
0,9604
|
7,5
|
56,25
|
|
136
|
31928
|
2223,04
|
2230,32
|
7,28
|
6,3
|
4,9784
|
0
|
340
|
Тогда, S 2 = 4,9784 /(20-2) = 0,27
Вычислим
оценку дисперсии групповой средней:
S 2 у’t = 20 = 0,27 –(1/20 +
(21 – 8,5)2/340) = 0,24
Тогда, S у’t = 20 = 0,48
Интервальная
оценка прогноза среднего значения объемов потребления определяется:
ух –tj;к
* S ух ≤у (20)≤ ух +tj;к
* S ух, (8)
Подставляя значения в полученное неравенство, имеем:
138,94 – 1,94 * 0,48 ≤ у (20) ≤ 138,94 +
1,94 * 0,48,
Или
138 ≤ у(20) ≤ 139,87
Для
нахождения интервальной оценки прогноза индивидуального значения У* (20)
вычислим дисперсию его оценки:
S 2у0 = 0,24 *(1+1/20 +(2007- 1995,5)2
)= 31,99
Тогда,
S у0 = 5,65
Доверительный
интервал для прогнозов индивидуального значения:
ух0 –tj;к
* S ух0 ≤у (20)≤ ух0 +tj;к
* S ух0, (9)
279,29 – 0,73 * 5,65 ≤ у (20) ≤ 279,29 +
0,73 * 5,65,
275,17≤ у (20) ≤ 283,41