Содержание
Введение. 3
1. Виды выборочного изучения. 6
2. Принцип «гнезд» как вид
классификации генеральной совокупности 10
3. Использование «гнездового»
способа в многоступенчатой комбинированной выборке. 13
4. Ошибки выборок. 18
5. Определение необходимого объема выборки. 22
Заключение. 23
ЛИТЕРАТУРА.. 26
Введение.
В связи с тем, что статистика имеет дело с массовыми
явлениями, статистические исследования весьма трудоемки и дороги. Поэтому давно
возникла мысль заменить сплошное наблюдение выборочным. Важная роль в
формировании выборочного метода наблюдения принадлежит работам Якоба Бернулли
(1654-1705). Весомый вклад в разработку теоретических основ выборочного метода
внесли русские математики - П.Л. Чебышев, А.М. Ляпунов, А.А. Марков. Российская
статистика имеет немалые заслуги в практическом применении выборочного метода.
В последние годы выборочные обследования стали
широко применяться в работе органов государственной статистики. Крупные и
средние предприятия охватываются сплошным наблюдением за их деятельностью, а
наблюдение за деятельностью малых предприятий производится с помощью выборочных
обследований.
Применение выборочного наблюдения взамен сплошного
дает возможность лучше организовать наблюдение, обеспечивает быстроту проведения
наблюдения, приводит к экономии средств и затрат труда на получение и обработку
информации.[1]
Множество всех единиц совокупности, обладающих
определенным признаком и подлежащих изучению, носит в статистике название
генеральной совокупности.
На практике по тем или иным причинам не всегда
возможно или же нецелесообразно рассматривать всю генеральную совокупность.
Тогда ограничиваются изучением лишь некоторой части ее, конечной целью которого
является распространение полученных результатов на всю генеральную
совокупность, т. е. применяют выборочный метод.
Для этого из генеральной совокупности особым образом
отбирается часть элементов, так называемая выборка, и результаты обработки
выборочных данных (например, средние арифметические значения) обобщаются на всю
совокупность.
Теоретической основой выборочного метода является
закон больших чисел. В силу этого закона при ограниченном рассеивании признака
в генеральной совокупности и достаточно большой выборке с вероятностью, близкой
к полной достоверности, выборочная средняя может быть сколь угодно близка к
генеральной средней. Закон этот, включающий в себя группу теорем, доказан
строго математически. Таким образом, средняя арифметическая, рассчитанная по
выборке, может с достаточным основанием рассматриваться как показатель,
характеризующий генеральную совокупность в целом.
Разумеется, не всякая выборка может быть основой для
характеристики всей совокупности, к которой она принадлежит. Таким свойством
обладают лишь репрезентативные (представительные) выборки, т. е. выборки,
которые правильно отражают свойства генеральной совокупности. Существуют
способы, позволяющие гарантировать достаточную репрезентативность выборки. Как
доказано в ряде теорем математической статистики, таким способом при условии
достаточно большой выборки является метод случайного отбора элементов
генеральной совокупности, такого отбора, когда каждый элемент генеральной
совокупности имеет равный с другими элементами шанс попасть в выборку. Выборки,
полученные таким способом, называются случайными выборками. Случайность выборки
является, таким образом, существенным условием применения выборочного метода
Так, при организации выборочного обследования и
формировании выборки из имеющихся сплошных данных исследователь располагает
определенной свободой маневра для обеспечения репрезентативности выборок. При
этом он может опираться на хорошо разработанную в математической статистике
теорию, методику и технику получения таких выборок.
При оперировании же данными ранее проведенных
выборочных обследований следует проверить, в какой мере они были выполнены в
соответствии с требованиями, предъявляемыми к выборочному методу. Для этого
надо знать, как было проведено это обследование. Чаще всего это вполне можно
сделать.
И совсем иное дело — естественные выборки данных.
Прежде всего необходимо доказать их репрезентативность. Без этого экстраполяция
показателей выборок на всю изучаемую совокупность будет необоснованной.
Поскольку пока еще нет достаточно надежных методов математической проверки
репрезентативности естественных выборок, то решающую роль здесь играет
выяснение истории их возникновения и содержательный анализ имеющихся данных.
1. Виды выборочного
изучения.
В зависимости от того, как осуществляется отбор
элементов совокупности в выборку, различают несколько видов выборочного
обследования. Отбор может быть случайным, механическим, типическим и серийным.
Случайным является такой отбор, при котором все
элементы генеральной совокупности имеют равную возможность быть отобранными.
Другими словами, для каждого элемента генеральной совокупности обеспечена
равная вероятность попасть в выборку.
Требование случайности отбора достигается на
практике с помощью жребия или таблицы случайных чисел.
При отборе способом жеребьевки все элементы
генеральной совокупности предварительно нумеруются и номера их наносятся на
карточки. После тщательной перетасовки из пачки любым способом (подряд или в
любом другом порядке) выбирается нужное число карточек, соответствующее объему
выборки. При этом можно либо откладывать отобранные карточки в сторону (тем
самым осуществляется так называемый бесповторный отбор), либо, вытащив
карточку, записать ее номер и возвратить в пачку, тем самым давая ей
возможность появиться в выборке еще раз (повторный отбор). При повторном отборе
всякий раз после возвращения карточки пачка должна быть тщательно перетасована.
Способ жеребьевки применяется в тех случаях, когда
число элементов всей изучаемой совокупности невелико. При большом объеме
генеральной совокупности осуществление случайного отбора методом жеребьевки
становится сложным. Более надежным и менее трудоемким в случае большого объема
обрабатываемых данных является метод использования таблицы случайных чисел.
Для очень больших совокупностей отбор с помощью
таблицы случайных чисел становится трудно осуществимым, так как сложно
перенумеровать всю совокупность. Здесь лучше применить механический отбор.
Механический отбор производится следующим образом.
Если формируется 10%-ная выборка, т. е. из каждых десяти элементов должен быть
отобран один, то вся совокупность условно разбивается на равные части по 10
элементов. Затем из первой десятки выбирается случайным образом элемент.
Например, жеребьевка указала девятый номер. Отбор остальных элементов выборки
полностью определяется указанной пропорцией отбора N номером первого
отобранного элемента. В рассматриваемом случае выборка будет состоять из
элементов 9, 19, 29 и т. д.
Механическим отбором следует пользоваться осторожно,
так как существует реальная опасность возникновения так называемых систематических
ошибок. Поэтому прежде чем делать механическую выборку, необходимо
проанализировать изучаемую совокупность. Если ее элементы расположены случайным
образом, то выборка, полученная механическим способом, будет случайной. Однако
нередко элементы исходной совокупности бывают частично или даже полностью
упорядочены. Весьма нежелательным для механического отбора является порядок
элементов, имеющий правильную повторяемость, период которой может совпасть с
периодом механической выборки. [2]
Нередко элементы совокупности бывают упорядочены по
величине изучаемого признака в убывающем или возрастающем порядке и не имеют
периодичности. Механический отбор из такой совокупности приобретает характер
направленного отбора, так как отдельные части совокупности оказываются
представленными в выборке пропорционально их численности во всей совокупности,
т. е. отбор направлен на то, чтобы сделать выборку представительной.
Механический отбор, как никакой другой, широко
использовался в русской и советской статистике.
Другим видом направленного отбора является
типический отбор. Следует отличать типический отбор от отбора типичных
объектов. Отбор типичных объектов применялся в земской статистике, а также при
бюджетных обследованиях. При этом отбор «типичных селений» или «типичных
хозяйств» производился по некоторым экономическим признакам, например по
размерам землевладения на двор, по роду занятий жителей и т. п. Отбор такого
рода не может быть основой для применения выборочного метода, так как здесь не
выполнено основное его требование — случайность отбора.
При собственно типическом отборе в выборочном методе
совокупность разбивается на группы, однородные в качественном отношении, а
затем уже внутри каждой группы производится случайный отбор. Типический отбор
организовать сложнее, чем собственно случайный, так как необходимы определенные
знания о составе и свойствах генеральной совокупности, но зато он дает более
точные результаты.
При серийном отборе вся совокупность разбивается на
группы (серии). Затем путем случайного или механического отбора выделяют
определенную часть этих серий и производят их сплошную обработку. По сути дела,
серийный отбор представляет собой случайный или механический отбор,
осуществленный для укрупненных элементов исходной совокупности.
Точность выборки зависит от схемы отбора. Выборка
может быть проведена по схеме повторного и беcповторного отбора.
Повторный отбор. Каждая отобранная единица, или серия возвращается во
всю совокупность и может вновь попасть в выборку. Это так называемая схема возвращенного
шара.
Бесповторный
отбор. Каждая обследованная
единица изымается и не возвращается в совокупность, поэтому она не попадает в
повторное обследование. Эта схема получила название невозвращеного
шара.
Рассмотренные виды отборов могут применяться в
комбинации. Комбинированный отбор может проходить в одну или несколько
ступеней.
Выборка называется одноступенчатой,
если отобранные однажды единицы совокупности подвергаются изучению.
Выборка называется многоступенчатой,
если отбор совокупности походит по ступеням, последовательным
стадиям, причем каждая ступень, стадия отбора имеет свою единицу отбора.
Многофазная
выборка характеризуется тем,
что на всех ступенях выборки сохраняется одна и та же единица отбора, но
проводится несколько стадий, фаз выборочных обследований, которые различаются
между собой широтой программы обследования и объемом выборки.
2. Принцип «гнезд»
как вид классификации генеральной совокупности
Существуют
два основных вида классификации (группировки) генеральной совокупности:
районирование (стратификация) и кластеризация (метод гнезд, серийная выборка).
Районированная (стратификационная) выборка
предполагает предварительную группировку единиц генеральной совокупности по
различающимся между собой типам.
В основу классификации закладывается признак (или
совокупность признаков), по которому респонденты существенно отличаются друг от
друга, и при этом именно данный признак, по мнению исследователя, может
существенно влиять на изучаемое явление. Таким образом, при выборе критерия
стратификации (районирования) исследователь руководствуется двумя
особенностями:
1) данная характеристика должна влиять на изучаемое
явление;
2) по данной характеристике единицы совокупности
должны различаться.
Например, при изучении отношения к приватизации
можно предположить, что тип предприятия, на котором работают респонденты
(государственное или частное), будет существенно сказываться на их отношении к
приватизации. Исследователь также знает, что доля людей, работающих на частных
предприятиях, незначительна, и при механическом случайном отборе вероятность их
попадания в выборку достаточно низкая. В таком случае все предприятия
разделяются на группы в зависимости от формы собственности, а потом из каждого
типа отбираются респонденты пропорционально численности данного контингента в
генеральной совокупности. В большинстве крупномасштабных опросов общественного
мнения по национальным выборкам первичная стратификация осуществляется по
географической локализации респондентов (отсюда и синонимичное название этого
принципа — районирование).
В статистическом смысле районирование соответствует
выделению такого числа и таких статистически однородных групп, чтобы дисперсия
заданных параметров внутри полученных групп была меньше, чем между ними.
Кластерный («гнездовой») способ предварительной
классификации объекта в определенном смысле противоположен районированному.
Если при районировании исследователь выделяет разнотипные подсовокупности, то
при гнездовой выборке генеральная совокупность разбивается на однотипные группы
(«гнезда»), внутри которых содержатся разнородные единицы наблюдения. Гнездо –
единица отбора высшей ступени, состоящая из более мелких единиц низшей ступени.
В качестве таких «гнезд» могут выступать школы, предприятия, семьи, коллективы,
почтовые отделения, избирательные участки и т.п. организации, интегрирующие тем
или иным образом группы людей, если исследователь считает, что эти кластеры
достаточно однотипны.
Используя принцип кластеризации, исследователь
должен руководствоваться тремя основными положениями:
1) все единицы генеральной совокупности должны быть
распределены между «гнездами»;
2) основные характеристики «гнезд» должны быть
максимально идентичными по заданным параметрам, т.е. различия между гнездами
должны быть минимальными, а составляющие их единицы по возможности более
неоднородные.
3) большое число малых гнезд предпочтительнее малого
числа крупных.
При использовании гнездовой выборки, в рамках
«гнезда» можно осуществлять сплошной опрос, а можно выборочный; это зависит от
численности и однородности совокупностей «гнезд».
Число единиц, образующих гнездо, называют его
размером.
Гнездовой отбор обладает большими организационными
преимуществами перед отбором элементарных единиц. Гнездовая выборка является
удобной и экономичной формой отбора.[3]
3. Использование
«гнездового» способа в многоступенчатой комбинированной выборке
Обычно районированный и гнездовой подходы в
научно-методической литературе противопоставляются друг другу. Но в современной
практике проведения массовых крупномасштабных исследований при построении
выборки чаще всего используются оба этих принципа. Применяя последовательно на
разных ступенях отбора каждый из этих принципов, исследователь добивается
повышения репрезентативности выборочной совокупности по различным
характеристикам, которые, по мнению исследователя, могут оказывать
принципиальное влияние на изучаемое явление.
Приведем несколько примеров подготовки выборки с
комментариями, поясняющими соображения, которыми руководствуется исследователь,
последовательно реализуя описанные выше принципы на каждой из ступеней отбора.
1. Например, социолог предполагает исследовать
профессиональные ориентации старшеклассников, в частности, ориентации на
поступление в вуз. Казалось бы, в данном случае на первой ступени целесообразно
применить гнездовую выборку, и в качестве «гнезд» рассматривать школы, часть
которых следует в случайном порядке отобрать как основу будущей выборочной
совокупности. Однако исследователь принимает во внимание следующие
обстоятельства:
1) существуют специальные школы (математические, с
углубленным изучением иностранных языков и т.п.), контингент которых в большей
степени ориентирован на вуз;
2) таких школ немного в общем перечне школ, и
поэтому существует достаточно высокая вероятность, что они не попадут в выборку
«гнезд». Учитывая, что школы, контингент которых в большей степени ориентирован
на вуз, может оказаться за пределами выборки, что, несомненно, скажется на
данных, касающихся профессиональных ориентаций старшеклассников, автор проекта
принимает решение — в качестве первого шага произвести районирование
(стратификацию) по этому показателю. Специальные школы выписываются в отдельный
список (перечень). В дальнейшем «гнезда» (школы) выбираются из каждого списка
отдельно, пропорционально численности старшеклассников в каждой из двух
полученных подсовокупностей (общие школы, специальные школы).
Естественно, что в основу районирования
(стратификации) генеральной совокупности старшеклассников исследователь может
заложить и другие критерии, например, тип городского района (индустриальный,
культурно-административный, «спальный» и т.п.), если он считает, что школы
разных районов не являются достаточно идентичными «гнездами»; и различия между
ними могут принципиально сказываться на результатах опроса. В итоге, на первой
ступени отбора генеральная совокупность стратифицируется (реализуется принцип
районирования), а на второй, когда исследователь считает, что в рамках каждой
страты «гнезда» достаточно идентичны с точки зрения целей исследования,
производится случайный отбор намеченного числа «гнезд» (школ). В дальнейшем
исследователь может в каждой школе проводить сплошной опрос старшеклассников, а
может, пользуясь принципом гнездового метода, отобрать классы.
Сколько следует отбирать школ, сколько классов,
сколько учеников опрашивать в каждом классе? Решение этих вопросов в каждом
исследовании — это поиск компромисса между требованиями теории (учет всех
признаков, дифференцирующих единицы наблюдения и отбора, а также дисперсии этих
признаков) и практическими возможностями организации исследования. Понятно,
что, чем меньше школ, тем легче организовать опрос. Но в таком случае
существенное влияние на выборочную совокупность могут оказать особенности школ,
не учтенные исследователем.
2. Сочетание районированного (стратификационного) и
кластерного («гнездового») подходов обычно используется и при построении
территориальных выборок, по которым проводятся массовые опросы общественного
мнения. Например, исследователь предполагает провести опрос населения по
репрезентативной общенациональной выборке Украины.
Если бы он хотел составить случайную одноступенчатую
выборку взрослого населения Украины (старше 18 лет), ему требовалось бы
составить список всех избирателей (более 37 млн человек) и с заданной ошибкой
репрезентативности отобрать из общего списка, пользуясь таблицей случайных
чисел, требуемое количество единиц наблюдения (например, при средней
ошибке — 3% требуется опросить 1800 человек). На такую процедуру не идет
ни один исследователь. Во-первых, сбор и составление общего перечня единиц
наблюдения — процедура очень трудоемкая, наталкивающаяся практически на
непреодолимые препятствия. Но даже если ее осуществить, то в результате будет
получено очень рассеянное в пространстве поле выборочной совокупности.
Практически невозможно будет найти интервьюеров, которые согласятся проводить
опрос 10-15 человек, локализованных на значительном расстоянии друг от друга. А
если бы такие интервьюеры и нашлись, то существенно возрастают транспортные
расходы. Учитывая, что на результате обязательно скажется «недостижимость»
части отобранных единиц наблюдения, что в конечном итоге все равно нарушит
принцип «равной вероятности попадания каждой единицы генеральной совокупности в
выборку», приступать к такой работе (подготовке одноступенчатой случайной выборки
взрослого населения Украины) нецелесообразно.
Поэтому исследователь сразу решает строить
многоступенчатую выборку. Теоретически здесь лучше применять гнездовой подход,
и в качестве «гнезда» использовать избирательные участки (ЖЭКи, почтовые
отделения). Это несколько бы упростило процедуру, по сравнению с
одноступенчатой случайной выборкой, но в принципе те же организационные
проблемы также стояли бы перед исследователем. Кроме того, он лишается
возможности сопоставлять результаты исследования по различным регионам, так как
их репрезентация не предусмотрена проектом выборки.
Для оптимизации процесса организации исследования
при построении территориальной выборки обычно на первом этапе производят
районирование: определяют типы регионов таким образом, чтобы можно было
сказать, что население одного типа региона достаточно однородно по какому-либо
признаку (признакам), а между населением разных типов существуют различия по
этому признаку. Затем каждую административно-политическую единицу (область или
район) относят к одному из выделенных типов. В основу типологии берется признак
или комплекс признаков, которые, по мнению исследователя, могут существенно
влиять на особенности изучаемого явления. Такими критериями типологии могут
выступать социально-культурные особенности населения, сложившиеся исторически,
особенности этнического состава населения административных подразделений,
политические ориентации (выявленные в ходе выборов или референдумов). Таким
образом, критерий типологии определяется в основном предметом исследования и
компетентностью автора проекта выборки. Критерий типологии должен быть
обоснован в проекте выборки. В дальнейшей работе из каждой страты (типа
региона) исследователь будет отбирать число единиц наблюдения, пропорциональное
численности населения регионов.
Второй шаг обычно также предусматривает дальнейшее
районирование, так как исследователь знает, что обычно тип поселения может
существенно сказываться на результатах исследования. Эта типология может быть
произведена с различной степенью точности: например, можно выделить два типа
(городское и сельское население); можно произвести более тонкую дифференциацию,
учитывая численность населенных пунктов, их специализацию в народном хозяйстве
и т.д. и т.п. Здесь опять исследователь ищет компромиссное решение: чем больше
типов и признаков заложено в основу типологизации, тем меньше будет ошибка
репрезентативности, но тем больший объем выборочной совокупности придется
формировать, чтобы наполнить полученные типы. В рабочем плане выборки
исследователь определяет численность выборочной подсовокупности каждого типа
населенного пункта.
В дальнейшей процедуре все населенные пункты,
распределенные по типам, в рамках каждого типа рассматриваются как равноценные
«гнезда», из которых производится отбор необходимого числа населенных пунктов.
Следующая ступень может также осуществляться
«гнездовым» способом, где в качестве «гнезда» выступают избирательные участки
(жэки, почтовые отделения). Эти организации удобно рассматривать в качестве
«гнезд», поскольку, во-первых, они располагают списками единиц наблюдения, а
во-вторых, достаточно однородны по своей внутренней структуре. Если
исследователь считает, что они не однородны по какому-то важному для
исследования качеству, то на третьей ступени он может еще раз произвести
районирование (стратификацию) в рамках каждого из населенных пунктов. Из
окончательно стратифицированной совокупности кластеров («гнезд») производится
их отбор в выборочную совокупность. Все страты и кластеры на различных ступенях
представляют собой единицы отбора.
На последней ступени осуществляется отбор единиц
наблюдения. Эта процедура может осуществляться различными техниками случайного
отбора. [4]
4.
Ошибки выборок
Между характеристиками выборочной
совокупности и искомыми характеристиками (параметрами) генеральной
совокупности, как правило, существует некоторое расхождение, которое называют
ошибкой. Общая величина возможной ошибки выборочной характеристики слагается из
ошибок двоякого рода ошибки регистрации и ошибки репрезентативности.
Ошибки
регистрации свойственны
любому статистическому наблюдению вообще и появление их может быть вызвано
несовершенством измерительных приборов, недостаточной квалификацией
наблюдателя, неточностью подсчетов и т.п.
Можно полагать, что по сравнению со
сплошным наблюдениями опасность возникновения ошибок регистрации при проведении
выборочных наблюдений должна быть меньше, так как выборочные наблюдения
проводятся с участием более квалифицированных работников и, следовательно,
более тщательно. Значительно уменьшается при выборочном наблюдении и опасность
преднамеренных искажений данных, так как специально подобранные и обученные
наблюдатели в них не заинтересованы.
Ошибки
репрезентативности присущи только
несплошным наблюдениям и представляют собой расхождение между величиной
полученных по выборке показателей и величиной этих показателей, которые были бы
получены при проведенном с одинаковой степенью точное при сплошном наблюдении.
Ошибки репрезентативности могут
быть систематическими и случайными.
Систематические
ошибки могут возникать в связи
с особенностями принятой системы отбора и обработки данных наблюдений или в
связи с нарушением установленных правил отбора.
Возникновение случайных ошибок
репрезентативности объясняется недостаточно равномерным
представлением в выборочной совокупности различных категорий единиц генеральной
совокупности, в силу чего распределение отобранной совокупности единиц не
вполне точно воспроизводит распределение единиц генеральной совокупности.
Определение возможной и фактически
допущенной ошибки выборки имеет важное значение при применении выборочного
метода. Величина ошибки характеризует степень надежности результатов выборки;
знание этой величины необходимо при оценке параметров генеральной совокупности.
Оценки возможной величины и состава ошибок репрезентативности ложатся в основу
планирования проектируемого выборочного наблюдения.
Величина случайной ошибки
репрезентативности зависит:
1.
От принятого
способа формирования выборочной совокупности. Выбор последнего связан с
решением вопросов о единице отбора, способе отбора единиц, способе размещения
всего объема отбираемых единиц по различным группам генеральной совокупности;
2.
От объема
выборки;
3.
От степени
колеблемости изучаемого признака в генеральной совокупности.
При серийной (гнездовой) выборке величина
ошибки выборки зависит не от числа обследованных единиц, а от числа
обследованных серий (s) и от величины межгрупповой дисперсии:
.
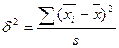Серийная выборка в основном
проводится как бесповторная, и формула ошибки выборки в этом случае имеет
следующий вид:
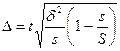
где s - число отобранных серий;
S - число серий в генеральной
совокупности.
Установленный предел Δ для ошибки выборки лишь
указывает, что если из генеральной совокупности сделать много выборок, то для
подавляющего большинства из них ошибка выборки не превысит вычисленного нами
предела Δ. При этом, правда, могут быть все-таки и такие выборки, у
которых ошибка выборки больше Δ, и не исключено, что конкретная выборка
входит в их число. Однако можно точно измерить степень уверенности в том, что
ошибка конкретной выборки не превысит Δ. Для этого нужно указать долю
выборок, у которых ошибка выборки не превосходит Δ. Обозначим эту долю
выборок через Р, где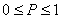 
. Чем
ближе Р к единице, тем больше будет уверенность в том, что ошибка конкретной
выборки не превышает ΔНа практике используются, например, значения, равные
0,68; 0,95; 0,99 и некоторые другие.Разумеется, всегда желательно обеспечить
большую надежность результатов, поэтому надо стараться выбрать Р возможно ближе
к 1. Однако необходимо учитывать, что с возрастанием надежности увеличивается и
t, а значит, и предельная ошибка Δ=tμ, т. е. падает точность
результатов, что может оказаться по тем или иным соображениям недопустимым.
Поэтому на практике приходится довольствоваться некоторым компромиссом между
противоречивыми требованиями максимальной надежности и максимальной точности.
Если такого компромисса достичь не удается и надежность и точность
неудовлетворительны, следует сделать вывод, что объем выборки недостаточен и
необходимо произвести новую выборку большего объема или же дополнить старую. [5]
Заметим, что стремясь к большей
точности и надежности результатов, не следует излишествовать в этом
направлении, так как может оказаться, что для достижения поставленных
требований придется брать выборку объемом во всю совокупность. При этом теряет
смысл само применение выборочного метода. Как правило, такие повышенные
требования к результатам не оправдываются целями исследования и без ущерба для
дела можно остановиться на более умеренных ограничениях. В том же случае, когда
высокие требования вытекают из целей исследования и вычисленный объем выборки
оказывается порядка объема всей совокупности, следует сделать вывод о том, что
в данном случае применение выборочного метода нецелесообразно. Отметим, что
приведенная формула дает общий объем выборки приближенно. Поэтому желательно
если есть возможность, еще несколько увеличить объем выборки по сравнению с
вычисленным.
5. Определение необходимого объема выборки
При проектировании выборочного
наблюдения с заранее заданным значением допустимой ошибки выборки очень важно
правильно определить численность (объем) выборочной совокупности, которая с
определенной вероятностью обеспечит заданную точность результатов наблюдения.
Формулы для определения необходимой численности выборки n легко получить
непосредственной из формул ошибок выборки.
Серийная выборка в основном
проводится как бесповторная, и формула
численности выборки в этом случае имеет следующий вид:
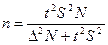
Эти формулы показывают, что с
увеличением предполагаемой ошибки выборки значительно уменьшается необходимый
объем выборки.
Заключение.
Сущность выборочного метода заключается в том, что
из генеральной совокупности извлекается часть элементов, выборка, на основании
параметров которой делаются выводы, относящиеся к генеральной совокупности.
Применение выборочного наблюдения взамен сплошного
дает возможность лучше организовать наблюдение, обеспечивает быстроту
проведения наблюдения, приводит к экономии средств и затрат труда на получение
и обработку информации.
Ключевая проблема выборочного исследования
заключается в получении репрезентативной (представительной выборки), по параметрам
которой можно объективно судить о характере параметров генеральной
совокупности.
Серийная («гнездовая») выборка является одним из
распространенных видов отбора.
При серийном отборе вся совокупность разбивается на
гнезда (кластеры) более мелких единиц. Затем путем случайного или механического
отбора выделяют определенную часть этих серий и производят их обработку. По
сути дела, серийный отбор представляет собой случайный или механический отбор,
осуществленный для укрупненных элементов исходной совокупности. В качестве таких «гнезд» могут выступать школы,
предприятия, семьи, коллективы, почтовые отделения, избирательные участки и
т.п. организации, интегрирующие тем или иным образом группы людей, если
исследователь считает, что эти кластеры достаточно однотипны.
В выборку могут быть включены как все единицы
низшего уровня, так и их часть.
Используя принцип кластеризации, исследователь
должен руководствоваться тремя основными положениями:
1) все единицы генеральной совокупности должны быть
распределены между «гнездами»;
2) основные характеристики «гнезд» должны быть
максимально идентичными по заданным параметрам, т.е. различия между гнездами
должны быть минимальными, а составляющие их единицы по возможности более
неоднородные.
3) большое число малых гнезд предпочтительнее малого
числа крупных.
Серийная выборка в основном
проводится как бесповторная, и формула ошибки выборки в этом случае имеет
следующий вид:
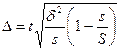
где s - число отобранных серий;
S - число серий в генеральной
совокупности.
Формула численности выборки имеет следующий вид:
.
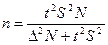В современной практике проведения массовых
крупномасштабных исследований при построении выборки чаще всего используются
комбинации гнездового подхода с
районированным. Применяя последовательно на разных ступенях отбора каждый из
этих принципов, исследователь добивается повышения репрезентативности
выборочной совокупности по различным характеристикам, которые, по мнению
исследователя, могут оказывать принципиальное влияние на изучаемое явление.
Гнездовой отбор обладает большими организационными
преимуществами перед отбором элементарных единиц. Гнездовая выборка является
удобной и экономичной формой отбора.
ЛИТЕРАТУРА
1.
Гришин А.Ф. Статистика: Учеб. Пособие. – М.:
Финансы и статистика, 2003.
2.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н.
Общая теория статистики: Учебник.-М.:ИНФРА – М., 1996.
3.
Ефремова М.Р. «Общая теория статистики»; М.:
«Инфра-М», 1996.
4.
Переяслова И.Г., Колбачев Е.Б., Переяслова О.Г. Статистика.
Серия «Высшее образование». – Ростов н/Д: «Феникс», 2003.
5.
Социально-экономическая статистика: Учебник для
вузов/Под ред. проф. Б.И.Башкатова. – М.: ЮНИТИ-ДАНА, 2002.
6.
Экономическая статистика (под. ред. Ю.Н. Иванова)
М.:ИНФРА-М, 1998.
[1]
Ефимова М.Р., Петрова Е.В.,
Румянцев В.Н. Общая теория статистики: Учебник.-М.:ИНФРА – М., 1996.- стр.95.
[2]
Экономическая статистика (под.
ред. Ю.Н. Иванова) М.:ИНФРА-М, 1998, стр.106.
[3]
Переяслова И.Г., Колбачев
Е.Б., Переяслова О.Г.Статистика.
Серия «Высшее образование». – Ростов н/Д: «Феникс», 2003.- стр.47.
[4]
Социально-экономическая
статистика: Учебник для вузов/Под ред. проф. Б.И.Башкатова. – М.: ЮНИТИ-ДАНА,
2002. – стр.237..
[5]
Социально-экономическая
статистика: Учебник для вузов/Под ред. проф. Б.И.Башкатова. – М.: ЮНИТИ-ДАНА,
2002. – стр.253.