МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Контрольная работа
По дисциплине: «Финансовая математика»
Вариант №7
Задание 1.
Требуется:
1)
Построить
адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора,
приняв параметры сглаживания α1=0,3; α2=0,6;
α3=0,3.
2)
Оценить
точность построенной модели с использованием средней относительной ошибки
аппроксимации.
3)
Оценить
адекватность построенной модели на основе исследования:
·
Случайности
остаточной компоненты по критерию пиков;
·
Независимости
уровней ряда остатков по d-критерию (критические значения d1 = 1,10 и d2 = 1,37) и по первому коэффициенту автокорреляции при
критическом значении r1=0,32.
·
Нормальности
распределения ряда остатков по критерию RS c критическими значениями от 3 до 4,21
4)
Построить
точечный прогноз на 4 шага вперед, т.е. на 1 год
5)
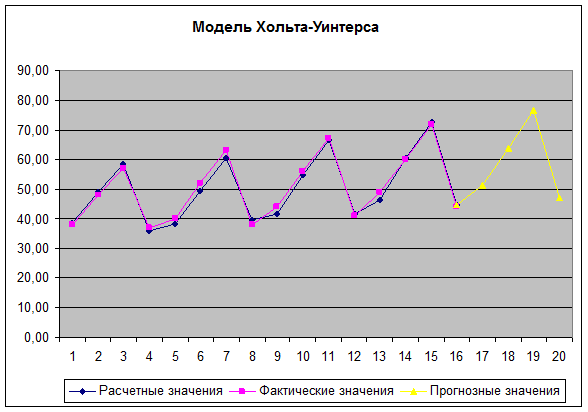
Построить
график, на котором должны быть отражены фактические, расчетные и прогнозные
значения.
Исходные данные
|
Квартал
|
Y(t)
|
|
1
|
38
|
|
2
|
48
|
|
3
|
57
|
|
4
|
37
|
|
5
|
40
|
|
6
|
52
|
|
7
|
63
|
|
8
|
38
|
|
9
|
44
|
|
10
|
56
|
|
11
|
67
|
|
12
|
41
|
|
13
|
49
|
|
14
|
60
|
|
15
|
72
|
|
16
|
44
|
|
|
806
|
В
первую очередь необходимо определить значения коэффициентов а(0) и b(0).
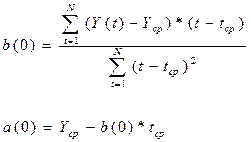
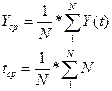
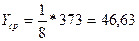
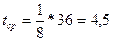
Находим:
1) 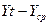
2) 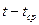
3)
(Y(t)-Yср)*(t-tср)
|
Квартал
|
Y(t)
|
Y(t)-Yср
|
t-tср
|
(Y(t)-Yср)*(t-tср)
|
(t-tср)2
|
Y(t)рег
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
38
|
-8,63
|
-3,50
|
30,19
|
12,25
|
44,00
|
|
2
|
48
|
1,38
|
-2,50
|
-3,44
|
6,25
|
44,75
|
|
3
|
57
|
10,38
|
-1,50
|
-15,56
|
2,25
|
45,50
|
|
4
|
37
|
-9,63
|
-0,50
|
4,81
|
0,25
|
46,25
|
|
5
|
40
|
-6,63
|
0,50
|
-3,31
|
0,25
|
47,00
|
|
6
|
52
|
5,38
|
1,50
|
8,06
|
2,25
|
47,75
|
|
7
|
63
|
16,38
|
2,50
|
40,94
|
6,25
|
48,50
|
|
8
|
38
|
-8,63
|
3,50
|
-30,19
|
12,25
|
49,25
|
|
|
373
|
|
|
31,50
|
42,00
|
|
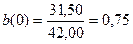
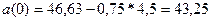
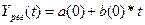 (в таблице)
(в таблице)
Далее нужно рассчитать значения сезонного коэффициента
F(-3), F(-2), F(-1) и F(0).
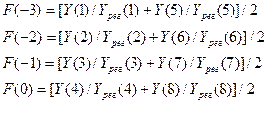
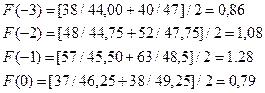
|
Квартал
|
F(t)
|
|
-3
|
0,86
|
|
-2
|
1,08
|
|
-1
|
1,28
|
|
0
|
0,79
|
Находим коэффициент Yp(1), при t=0, k=1, L=4
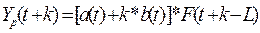
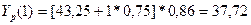
Находим
коэффициента a(1), b(1).
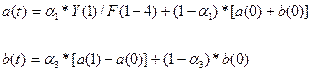
а(1) = 0,3*38/0,86+0,7*44= 44,10
b(1) =0,3(44,10-43,25)+0,7*0,75= 0,78
при t=1
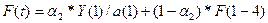
F(1) = 0,6*38 / 44,10+ 0,4* 0,86 = 22,8 / 44,44 = 0,86
Пологая,
что t=1, k=1, найдем Yp(2)
Yp(2) = [44,10+1*0,78]*1,08= 48,50
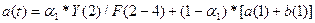
а(2) =
0,3*48/1,08+0,7*44,88= 44,74
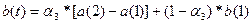
b(1) =0,3(44,74-44,10)+0,7*0,78 = 0,74
F(2) = 0,6*48 / 44,74+ 0,4* 1,08 = 1,08
Проверка точности модели.
Перед
тем, как строить прогноз построенной модели, нужно проверить на точность и адекватность.
Для
проверки модели на качество, в первую очередь рассчитывают остатки.
Е(t) =Y(t)-Yp(t) = 38-38,79 = -0,79
Для
того, чтобы условие в точности выполнялось, средняя относительная ошибка по
модели не должно превышать 5%
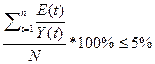
Проверка адекватности модели
Проверку
случайности уровней ряда остатков Е(t) проводят по критерию поворотных
точек, каждое следующее значение ряда остатков Е(t) сравнивают с двумя соседними
Если
оно больше (или меньше) обоих соседних значений, то точка считается поворотной
и обозначается цифрой 1. Общее число поворотных точек Р=5
Далее находим величину q
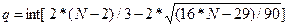
q= 2*14 / 3-2*√((16*16-29)/90) = 9,0
Так как
p=10>q=6, то значит условие случайности
уровней ряда остатков выполнено
Вывод:
так как число р=6 меньше критического значения q=6,16, то условие случайности ряда
остатков не выполняется.
Проверка
независимости уровней ряда (проверка на отсутствие автокорреляции)
По d-критерию Дарбина-Уотсона
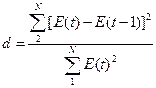
Значения
взяты с таблицы
d = 60.66/38.2 = 1.59
Если значение d>2 это означает, что имеет место отрицательная автокорреляция и
значение d
уточняется.
Если по
d- критерию
нельзя сделать вывод о независимости ряда остатков, то проводят проверку по
первому коэффициенту автокорреляции.
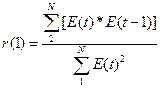 = 7,34/38,2 = 0,19
= 7,34/38,2 = 0,19
Проверка
уровней ряда остатков на нормальность распределения проводится по RS-критерию.
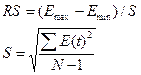
S= √(38,2/15) = 1,60
RS = (2.69-(-1.5))/1.6 = 2.63
Величина
RS сравнивается с
критическими табличными значениями RS1 и RS2.
-1.5<2.63<2.69
Вывод:
ряд остатков подчиняется нормальному распределению.
Все
проверки выполнены, можно приступать к построению прогноза.
Начиная
строить прогноз, делаем t=1…..16, k меняется по шагова.
При расчете значений Yp(17)- Yp(20)
коэффициент k
увеличивается на каждом шаге. Для расчета Yp(17)- Yp(20)
используем последние значения коэффициентов а(16) и b(16).
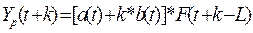
Yp(17)= (62,15+1*0,99)*0,81 = 51,36
Yp(18)= (62,15+2*0,99)*1 = 63,84
Yp(19)= (62,15+3*0,99)*1,17 = 76,51
Yp(20)= (62,15+4*0,99)*0,71 = 47,06
|
Фактические
значения
|
Расчетные
значения
|
Прогнозные
значения
|
|
38
|
38,61
|
0,00
|
|
48
|
49,18
|
0,00
|
|
57
|
58,38
|
0,00
|
|
37
|
36,04
|
0,00
|
|
40
|
38,14
|
0,00
|
|
52
|
49,47
|
0,00
|
|
63
|
60,60
|
0,00
|
|
38
|
39,50
|
0,00
|
|
44
|
41,72
|
0,00
|
|
56
|
54,73
|
0,00
|
|
67
|
66,59
|
0,00
|
|
41
|
41,72
|
44,83
|
|
49
|
46,31
|
51,36
|
|
60
|
60,34
|
63,84
|
|
72
|
72,44
|
76,51
|
|
44
|
44,83
|
47,06
|
|
Квар
|
Y(t)
|
Y(t)-Yср
|
t-tср
|
(Y(t)-Yср)*(t-tср)
|
(t-tср)2
|
Y(t)рег
|
a(t)
|
b(t)
|
F(t)
|
Yp(t)
|
E(t)
|
Точки поворота
|
E(t)2
|
[E(t)-E(t-1)]2
|
E(t)*E(t-1)
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
|
-3
|
|
|
|
|
|
|
|
|
0,77
|
|
|
|
|
|
|
|
|
-2
|
|
|
|
|
|
|
|
|
0,98
|
|
|
|
|
|
|
|
|
-1
|
|
|
|
|
|
|
|
|
1,17
|
|
|
|
|
|
|
|
|
0
|
|
|
|
|
|
|
50,13
|
0,25
|
0,73
|
|
|
|
|
|
|
|
|
1
|
38
|
-12,38
|
0,00
|
0,00
|
0,00
|
50,38
|
50,14
|
0,17
|
0,76
|
38,61
|
-0,61
|
*****
|
0,37
|
|
|
|
|
2
|
48
|
-2,38
|
1,00
|
-2,38
|
1,00
|
50,63
|
49,95
|
0,06
|
0,97
|
49,18
|
-1,18
|
0
|
1,40
|
0,33
|
0,72
|
|
|
3
|
57
|
6,62
|
2,00
|
13,24
|
4,00
|
50,88
|
49,66
|
-0,04
|
1,16
|
58,38
|
-1,38
|
1
|
1,90
|
0,04
|
1,63
|
|
|
4
|
37
|
-13,38
|
3,00
|
-40,14
|
9,00
|
51,13
|
50,01
|
0,08
|
0,73
|
36,04
|
0,96
|
0
|
0,93
|
5,49
|
-1,33
|
|
|
5
|
40
|
-10,38
|
4,00
|
-41,52
|
16,00
|
51,38
|
50,83
|
0,30
|
0,78
|
38,14
|
1,86
|
0
|
3,47
|
0,81
|
1,80
|
|
|
6
|
52
|
1,62
|
5,00
|
8,10
|
25,00
|
51,63
|
51,91
|
0,53
|
0,99
|
49,47
|
2,53
|
1
|
6,40
|
0,44
|
4,71
|
|
|
7
|
63
|
12,62
|
6,00
|
75,72
|
36,00
|
51,88
|
53,06
|
0,72
|
1,17
|
60,60
|
2,40
|
0
|
5,74
|
0,02
|
6,06
|
|
|
8
|
38
|
-12,38
|
7,00
|
-86,66
|
49,00
|
52,13
|
53,17
|
0,54
|
0,72
|
39,50
|
-1,50
|
1
|
2,25
|
15,16
|
-3,59
|
|
|
9
|
44
|
-6,38
|
8,00
|
-51,04
|
64,00
|
52,38
|
54,59
|
0,80
|
0,79
|
41,72
|
2,28
|
1
|
5,21
|
14,30
|
-3,42
|
|
|
10
|
56
|
5,62
|
9,00
|
50,58
|
81,00
|
52,63
|
55,78
|
0,92
|
1,00
|
54,73
|
1,27
|
0
|
1,61
|
1,03
|
2,89
|
|
|
11
|
67
|
16,62
|
10,00
|
166,20
|
100,00
|
52,88
|
56,80
|
0,95
|
1,18
|
66,59
|
0,41
|
0
|
0,17
|
0,74
|
0,52
|
|
|
12
|
41
|
-9,38
|
11,00
|
-103,18
|
121,00
|
53,13
|
57,44
|
0,86
|
0,72
|
41,72
|
-0,72
|
1
|
0,52
|
1,28
|
-0,30
|
|
|
13
|
49
|
-1,38
|
12,00
|
-16,56
|
144,00
|
53,38
|
59,32
|
1,16
|
0,81
|
46,31
|
2,69
|
1
|
7,24
|
11,66
|
-1,95
|
|
|
14
|
60
|
9,62
|
13,00
|
125,06
|
169,00
|
53,63
|
60,38
|
1,13
|
1,00
|
60,34
|
-0,34
|
0
|
0,11
|
9,18
|
-0,91
|
|
|
15
|
72
|
21,62
|
14,00
|
302,68
|
196,00
|
53,88
|
61,40
|
1,10
|
1,17
|
72,44
|
-0,44
|
0
|
0,19
|
0,01
|
0,15
|
|
|
16
|
44
|
-6,38
|
15,00
|
-95,70
|
225,00
|
54,13
|
62,15
|
0,99
|
0,71
|
44,83
|
-0,83
|
*****
|
0,68
|
0,15
|
0,36
|
44,83
|
|
17
|
|
|
|
|
|
|
|
|
|
51,36
|
|
|
|
|
|
51,36
|
|
18
|
|
|
|
|
|
|
|
|
|
63,84
|
|
|
|
|
|
63,84
|
|
19
|
|
|
|
|
|
|
|
|
|
76,51
|
|
|
|
|
|
76,51
|
|
20
|
|
|
|
|
|
|
|
|
|
47,06
|
|
|
|
|
|
47,06
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Суммы
|
806,00
|
|
|
304,40
|
1240,00
|
836,08
|
|
|
|
|
|
6,00
|
38,20
|
60,66
|
7,34
|
|
|
Таблица 2. Вспомогательные
данные
|
|
|
|
|
|
|
|
|
|
|
|
N
|
16,0000
|
|
Проверка
качества модели
|
|
|
L
|
4,0000
|
|
|
|
|
|
|
|
tср
|
1,0000
|
|
|
|
|
|
|
|
Yср
|
50,38
|
|
Точность
модели
|
|
|
OK
|
|
Альфа1
|
0,3000
|
|
Проверка
случайности ряда остатков E(t)
|
OK
|
|
Альфа2
|
0,6000
|
|
Проверка
независимости уровней ряда E(t)
|
OK
|
|
Альфа3
|
0,3000
|
|
|
по
критерию Дарбина-Уотсона
|
OK
|
|
k
|
1,0000
|
|
|
первый
коэффициент автокорреляции
|
OK
|
|
d1
|
1,1000
|
|
Проверка
нормальности распределения ряда E(t)
|
OK
|
|
d2
|
1,3700
|
|
|
|
|
|
|
|
r1
|
0,3200
|
|
|
|
|
|
|
|
RS1
|
-1,4987
|
|
|
|
|
|
|
|
RS2
|
2,6914
|
|
|
|
|
|
|
|
q
|
6,1570
|
|
|
|
|
|
|
|
p
|
6,0000
|
|
|
|
|
|
|
|
d
|
1,5879
|
|
|
|
|
|
|
|
r(1)
|
0,1922
|
|
|
|
|
|
|
|
S
|
1,5959
|
|
|
|
|
|
|
|
RS
|
2,6256
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 2
Даны
цены (открытия, максимальная, минимальная и закрытия) за 10дней. Интервал
сглаживания принять равным пяти дням. Рассчитать:
1) экпоненциальную
скользящую среднюю(ЕМА);
2)
момент;
3)
скорость изменения цен;
4)
индекс относительной силы;
5) % R, %K, %D.
Расчеты
проводить для всех дней, для которых эти расчеты можно выполнить на основании
имеющих данных.
|
|
Вариант
7.
|
|
Дни
|
Цены
|
|
|
Макс.
|
Мин.
|
Закр.
|
|
1
|
663
|
605
|
610
|
|
2
|
614
|
577
|
614
|
|
3
|
639
|
580
|
625
|
|
4
|
625
|
572
|
574
|
|
5
|
600
|
553
|
563
|
|
6
|
595
|
563
|
590
|
|
7
|
608
|
590
|
598
|
|
8
|
610
|
573
|
580
|
|
9
|
595
|
575
|
595
|
|
10
|
600
|
580
|
580
|
n=5
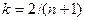
k= 0.33
1) Так
как известен интервал сглаживания и цена закрытия найдем простую скользящую
среднюю величину по формуле:
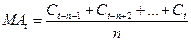
МА(5)=
(610+614+625+574+563)/5 = 2986/5 = 597,2
Затем
находим взвешенную скользящую среднюю величину WMAt
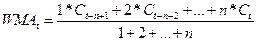
WMA(5) = (1*610+2*614+3*625+4*574+5*563)/15
= 8824/15 = 588.27
Экспоненциальная
скользящая средняя
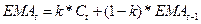
Для n=5, первое значение ЕМА, которую
нельзя рассчитать, будет равна МА5 = 597,2, далее ЕМА считается по формуле
ЕМА6=
1/3*590+(1-1/3)*597,2 = 594,8
ЕМА7 =
1/3*598+(1-1,3)*594,8 = 595,87
2) Для
определения момента купли или продажи ориентируются на взаимное расположение
двух скользящих средних с различными интервалами сглаживания.
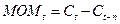
МОМ(6)
= С6-С(6-5) = С6-С1= 590-610 = -20
МОМ(7)
= С7-С2= 598-614 = -16
3)Рассчитываем
скорость изменение цен.
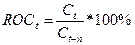
ROC(6) = C6/C1*100% = 590/610*100% = 96.72%
ROC(7) = C7/C2*100% = 598/614*100% = 97.39%
4)Индекс
относительной силы
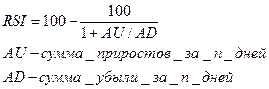
Находим
повышение и понижение цен, путем Сt-Ct-1
|
C(t)
|
Повышение
цены
|
Понижение
цены
|
|
4
|
11
|
12
|
|
610
|
|
|
|
614
|
4,00
|
|
|
625
|
11,00
|
|
|
574
|
|
51,00
|
|
563
|
|
11,00
|
|
590
|
27,00
|
|
|
598
|
8,00
|
|
|
580
|
|
18,00
|
|
595
|
15,00
|
|
|
580
|
|
15,00
|
AU – повышение цен за 5 дней
AD – понижение цен за 5 дней (в таблице)
RSI(6) = 100-(100/(1+42/62)) = 40,38
RSI(7) = 100-(100/(1+46/62)) = 42,59
RSI(8) = 100-(100/(1+35/80)) = 30,43
И т.
д., введены в таблице
5) % R, %K, %D.
Найдем maх(Н5) и min(L5) значения цен за n (5) дней
|
H5
|
L5
|
|
663,00
|
553,00
|
|
639,00
|
553,00
|
|
639,00
|
553,00
|
|
625,00
|
553,00
|
|
610,00
|
553,00
|
|
610,00
|
563,00
|
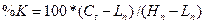 = 10/110*100% = 9,09%
= 10/110*100% = 9,09%
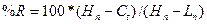 = 100/110*100% = 90,91%
= 100/110*100% = 90,91%
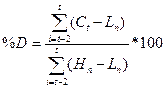
Для
удобства расчета найдем Сумма C(t)-L5
за 3 дня и Сумма H5-L5 за 3 дня
(с 5 по 7;с 6 по 8 и т.д.).
%D = 92/282*100%
= 32.62%
|
|
Цена
|
Индикаторы
|
|
Цена открытия
|
max
|
min
|
C(t)
|
MA(t)
|
WMA(t)
|
EMA(t)
|
MOM(t)
|
ROC(t)
|
Повышение цены
|
Понижение цены
|
AU
|
AD
|
RSI(t)
|
H5
|
L5
|
C(t)-L5
|
H5-C(t)
|
H5-L5
|
%K
|
%R
|
Сумма C(t)-L5 за
3 дня
|
Сумма H5-L5 за 3 дня
|
%D
|
Медленная %D
|
Зона
пере-проданности
|
Зона
пере-купленности
|
|
Дни (t)
|
1
|
2
|
3
|
4
|
5
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
|
1
|
|
663
|
605
|
610
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
614
|
577
|
614
|
|
|
|
|
|
4,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
639
|
580
|
625
|
|
|
|
|
|
11,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
625
|
572
|
574
|
|
|
|
|
|
|
51,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
600
|
553
|
563
|
597,20
|
588,27
|
597,20
|
|
|
|
11,00
|
|
|
|
663,00
|
553,00
|
10,00
|
100,00
|
110,00
|
9,09%
|
90,91%
|
|
|
|
|
|
|
|
6
|
591
|
595
|
563
|
590
|
593,20
|
585,87
|
594,80
|
-20,00
|
96,72
|
27,00
|
|
42,00
|
62,00
|
40,38
|
639,00
|
553,00
|
37,00
|
49,00
|
86,00
|
43,02%
|
56,98%
|
|
|
|
|
|
|
|
7
|
594
|
608
|
590
|
598
|
590,00
|
587,47
|
595,87
|
-16,00
|
97,39
|
8,00
|
|
46,00
|
62,00
|
42,59
|
639,00
|
553,00
|
45,00
|
41,00
|
86,00
|
52,33%
|
47,67%
|
92,00
|
282,00
|
32,62%
|
|
|
|
|
8
|
577
|
610
|
573
|
580
|
581,00
|
584,13
|
590,58
|
-45,00
|
92,80
|
|
18,00
|
35,00
|
80,00
|
30,43
|
625,00
|
553,00
|
27,00
|
45,00
|
72,00
|
37,50%
|
62,50%
|
109,00
|
244,00
|
44,67%
|
|
|
|
|
9
|
592
|
595
|
575
|
595
|
585,20
|
588,80
|
592,05
|
21,00
|
103,66
|
15,00
|
|
50,00
|
29,00
|
63,29
|
610,00
|
553,00
|
42,00
|
15,00
|
57,00
|
73,68%
|
26,32%
|
114,00
|
215,00
|
53,02%
|
|
|
|
|
10
|
0
|
600
|
580
|
580
|
588,60
|
587,07
|
588,03
|
17,00
|
103,02
|
|
15,00
|
50,00
|
33,00
|
60,24
|
610,00
|
563,00
|
17,00
|
30,00
|
47,00
|
36,17%
|
63,83%
|
86,00
|
176,00
|
48,86%
|
|
|
|
|
11
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интервал
сглаживания n=
|
5,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумма
от 1 до n
|
|
15,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэфф.
K для EMA
|
|
0,33
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание
3
Выполнить различные коммерческие расчеты, используя
данные, приведенные в таблице.
S = 3 500 000 (сумма средств в рублях)
Т лет = 5 (время в годах)
i=40 (ставка
в процентах)
m=4 (число
начислений)
Тн = 11.01.02. (дата начальная)
Тк = 19.03.02 (дата конечная)
Тдн = 90 (время в днях)
3.1 Банк выдал
ссуду, размером S руб. Дата
выдачи ссуды – Тн, возврата- Тк, День выдачи и день возврата считать за 1 день.
Проценты рассчитываются по простой процентной ставке i% годовых.
Найти:
3.1.1) точные проценты с точным числом дней ссуды (I);
3.1.2) обыкновенные проценты с точным числом дней
ссуды (I);
3.1.3) обыкновенные проценты с приближенным числом
дней ссуды (I).
Дано:
S = 3 500 000
Тн = 11.01.02
Тк = 19.03.02
i = 40
Решение:
3.1.1)
к=366
t= 20+28+19
= 67
I= 3 500 000 * 0,40*67/366 = 256 284,15
3.1.2)
к = 360
t = 67
I = 3 500 000 * 0,40*67/360 = 260 555, 56
3.1.3)
к=360
t = 19+30+19=68
I = 3 500 000* 0.40*68/360 = 264 444,44
Ответ: 3.1.1) 256 284,15; 3.1.2) 260 555,
56; 3.1.3) 272 222,22
3.2 Через Тдн
дней после подписания договора должник уплатит S руб. Кредит выдан под i% годовых
(проценты обыкновенные). Какова первоначальная сумма и дисконт?
Дано:
S = 3 500 000
Тдн = 90
i = 40
Решение:
S= P(1+ni)
P= S/(1+ni)
P=
3 500 000/(1+90/360*0.4) = 3 181 818,18
D= S –P = 3
500 000 - 3 181 818,18 = 318 181 .82
3.3 Через Tдн
предприятие должно получить по векселю S рублей. Банк приобрел этот вексель с дисконтом. Банк учел вексель по
учетной ставке i % годовых
(в году 360 дней). Определить полученную предприятием сумму и дисконт.
Дано:
n= 90/360
S = 3 500 000
i = 40%
Решение:
D=
3 500 000*0.4*90/360 = 350 000
P=S-D = 3 500 000 – 350 000 = 3 150 000
3.4 В
кредитном договоре на сумму S рублей и
сроком на Tлет лет,
зафиксирована ставка сложных процентов i% годовых. Определить наращенную сумму.
Дано:
S = 3 500 000 руб.
Тлет = 5 лет
i = 40%
Решение:
S = 3 500 000*(1+0,4)^5 = 18 823 840,00
3.5 Ссуда
размером S рублей предоставлена на Tлет.
Проценты сложные, ставка – i% годовых.
Проценты начисляются m раз в году. Вычислить наращенную сумму(S).
Дано:
S = 3 500 000 руб.
Тлет = 5 лет
i = 40%
m=4
Решение:
S = 3 500 000* (1+0.4/4) ^5*4 = 8 252 816,92
3.6 Вычислить
эффективную ставку процента, если банк начисляет проценты m раз в году исходя из номинальной ставки i% годовых.
Дано:
i = 40%
m=4
Решение:
Iэ =
[(1+0,4/4) ^4 – 1]*100% = 46,41%
Ответ: 46,41%
3.7.
Определить, какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную
ставку i% годовых.
Дано:
i = 40%
m=4
Решение:
I = 4[(1+0,4)^-4 -1] = 4[1/3,84 -1] = 35,10%
3.8 Через Tлет
предприятию будет выплачена сумма S рублей.
Определить ее современную стоимость при условии, что применяется сложная
процентная ставка i% годовых.
Дано:
S = 3 500 000 руб.
Тлет = 5 лет
i = 40%
Решение
S =
3 500 000/(1+0.4)^5 = 650 770.51
3.9 Через Tлет
по векселю должна быть выплачена сумма S рублей. Банк учел вексель по сложной учетной ставке i% годовых. Определить дисконт.
Дано:
S = 3 500 000 руб.
Тлет = 5 лет
i = 40%
Решение
D = S[1-(1-i)^5] = 3 500 000(1-(1-0,4)^5) = 3 227 840
3.10 В течение
Tлет на расчетный счет в конце каждого года поступает по S руб., на которые m раз в год начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном счете к концу указанного
срока.
Дано:
R = 3 500 000 руб.
Тлет = 5 лет
i = 40%
m=4
Решение:
S= R*((1+0.40/4)^20-1)/((1+0.4/4) ^4-1)= 3 500 000*((1.1)^20-1)/((1.1)^4-1)= 43 193 815,61
|
Сумма
|
Дата начальная
|
Дата конечная
|
Время в днях
|
Время в годах
|
Ставка
|
Число начислений
|
Точное число дней сделки
|
Приближенное число дней сделки
|
|
S
|
Tн
|
Tк
|
Tдн
|
Tлет
|
i
|
m
|
|
|
|
3500000
|
11.01.02
|
19.03.02
|
90
|
5
|
40,00%
|
4
|
67
|
70
|
|
|
|
|
|
|
|
|
|
|
1.
|
1.1 Точные с точным числом дней
|
256284,15
|
|
|
|
|
1.2 Обыкновенные с точным числом дней
|
260555,56
|
|
|
|
|
1.3 Обыкновенные с приближенным числом дней
|
272222,22
|
|
|
|
|
|
|
|
|
|
|
|
2.
|
Первоначальная сумма P
|
3181818,18
|
|
|
|
|
Дискнот D
|
350000
|
|
|
|
|
|
|
|
|
|
|
|
3.
|
Полученная сумма P
|
3150000
|
|
|
|
|
Дисконт D
|
350000
|
|
|
|
|
|
|
|
|
|
|
|
4.
|
Наращенная сумма S
|
18823840,0
|
|
|
|
|
|
|
|
|
|
|
|
5.
|
Наращенная сумма при начислении m раз в год
|
5636785
|
|
|
|
|
|
|
|
|
|
|
|
6.
|
Эффективная ставка процента iэ
|
46,41
|
|
|
|
|
|
|
|
|
|
|
|
7.
|
Номинальная ставка процента jном
|
4,12
|
|
|
|
|
|
|
|
|
|
|
|
8.
|
Современная стоимость при сложной ставке P
|
650770,51
|
|
|
|
|
|
|
|
|
|
|
|
9.
|
Дисконт D
|
3227840
|
|
|
|
|
|
|
|
|
|
|
|
10.
|
Сумма на расчетном счету
|
10240932,8
|
|
|
|
|
|
|
|
|
|
|
|
|