Министерство образования РФ

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Отчет по лабораторной работе

на тему: «Оптимизационные экономико-математические модели. Методы получения оптимизационных решений»

 

                                                          

 

      Исполнитель:

студентка 3 курса

Руководитель:

 

Омск - 2008

Вариант №7

 

 

 

 

ЗАДАЧА 1

Распределение рекламного бюджета

Фирма рекламирует свою продукцию с использованием четырёх средств: телевидения, радио, газет и афиш. Из различных рекламных экспериментов, которые проводились в прошлом, известно, что эти средства приводят к увеличению прибыли соответственно на 10, 3, 7 и 4 у.е., затраченную на рекламу.

Распределение рекламного бюджета по различным средствам подчинено следующим ограничениям:

а) полный бюджет не должен превосходить 500 000 у.е.;

б) следует расходовать не более 40% бюджета на телевидение и не более 20% бюджета на афиши;

в) вследствие привлекательности для подромтков радио на него следует расходовать по крайней мере половину того, что планируется на телевидение.

 

Решение:

Экономико-математическая модель

Обозначим через X₁, X₂, X₃, X₄  количество денежных средств, которые вкладываются в рекламу.

Целевая функция – это математическая запись критерия оптимальности, то есть выражение, которое необходимо максимизировать:

f(х)=10Х₁+3Х₂ +7Х₃+4Х₄.

Ограничения по ресурсам:

X₁ 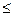 0,4(10X₁+3X₂+7X₃+4X₄)

X₄ 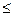 0,2(10X₁+3X₂+7X₃+4X₄)

Х₂ ³ 0,5X₁

_X ³ 0

Преобразуем:

-3Х₁-1,2Х₂-2,8Х₃-1,6Х₄ 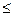 0

-2Х₁-0,6Х₂-1,4Х₃+0,2Х₄ 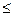 0

-0,5Х₁+Х₂ ³ 0

Х ³ 0

Приведем подробное описание технологии получения решения приведенной ЗЛП.

Обозначим: М1 – один щелчок левой кнопки мыши;

М2 – двойной щелчок левой кнопки мыши

Далее необходимо выполнить следующее:

1.          Создадим форму для ввода условий задачи. Запустим Excel, для этого выберем Microsoft Excel из подменю Программы главного меню Windows. Открывается чистый лист Excel. Создадим текстовую форму – таблицу для ввода условий задачи (рис. 1.1).

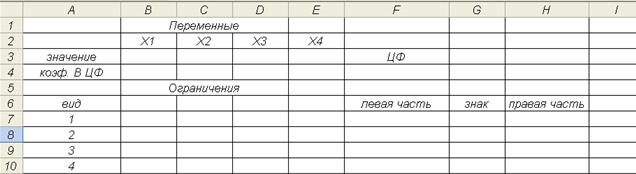
Рис. 1.1

2.          Укажем адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначим через Х₁, Х_2, Х₃, Х₄ количество денежных средств, которые вкладываются в рекламу. В нашей задаче оптимальные значения компонент вектора Х=( Х₁, Х_2, Х₃, Х₄) будут помещены в ячейках В3:E3, оптимальное значение целевой функции – в ячейке F4.

3.          Введем исходные данные задачи в созданную форму – таблицу, представленную на рис.1.2. Сохраним таблицу.

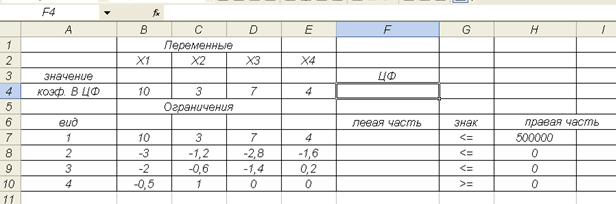
Рис 1.2

4.          Введем зависимость для целевой функции:

-         курсор в ячейку D4;

-         курсор на кнопку «Мастер функций», расположенную на панели инструментов;

-         М1. На экране появляется диалоговое окно Мастер функций шаг 1 из 2 (рис. 1.3);

-         Курсор в окно “Категория” на категорию Математические;

-         М1;

-         Курсор в окно Функции на СУММПРОИЗВ;

-         М1. На экране появляется диалоговое окно СУММПРОИЗВ (рис. 1.4);

-         В строку “Массив 1” ввести В$3:Е$3;

-         В строку «Массив 2» ввести B4:Е4;

-         Кнопка «ОК». На экране: в ячейку F4 введена функция (рис. 1.5).

5.     Введем зависимости для ограничений:

-         курсор в ячейку D4;

-         на панели инструментов кнопка Копировать в буфер → М1;

-         курсор в ячейку D7;

-         на панели инструментов кнопка Вставить из буфера → М1

В строке Меню указатель мыши на имя Сервис → М1. В развернутом меню команда Поиск решения → М1. Появляется диалоговое окно Поиск решения  (рис. 7).

6.          Назначим целевую функцию (установим целевую ячейку):

-   курсор в строку Установить целевую ячейку;

-   введем адрес ячейки $D$4;

-   введем направление целевой функции в зависимости от условия задачи – Максимальному значению;

-   курсор в строку Изменяя ячейки;

-   введем адреса искомых переменных  B$3:C$3.

7.          Введем ограничения:

-   указатель мыши на кнопку Добавить → М1. Появляется диалоговое окно Добавление ограничения (рис. 8);

-   в строке Ссылка на ячейку введем адрес $D$7;

-   введем знак ограничения ≤;

-   в строке Ограничение введем адрес $F$7;

-   указатель мыши на кнопку Добавить → М1. На экране вновь диалоговое окно Добавление ограничения ;

-   введем остальные ограничения задачи по вышеописанному алгоритму. В строке Ссылка на ячейку введем адрес $D$8, в строке Ограничение введем $F$8 (рис 9);

-   после введения последнего ограничения кнопка ОК.

На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 10).

8.     Введем параметры для решения ЗЛП:

-         в диалоговом окне указатель мыши на кнопку Параметры поиска решения (рис. 11);

-         установим флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения

-         указатель мыши н кнопку Выполнить.

Через непродолжительное время появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками В3:С3 для значений Хi  и ячейка D4 с максимальным значением целевой функции (рис 12).

-         кнопка ОК.

Появились три типа отчета: отчет по результатам, отчет по пределам, отчет по устойчивости (см. рис 13,14,15).

В таблице в ячейке D4 появилось значение 8,57143, в ячейках D7, D8 соответственно 20 и 22,8571, в ячейках В3:С3 значения 0 и 2,8571429 (рис. 6).

Полученное решение означает, что максимальный доход – 8,57143 тыс.руб при выпуске и реализации 0шт стульев и 5,8271429шт столов.

0х1+2,8571429х3=8,57143

При этом все трудовые ресурсы и фонд рабочего времени оборудования будут использованы полностью.

 

 

 

ЗАДАЧА 2

В распоряжении некоторой компании имеется 6 торговых точек и 5 продавцов. Из прошлого опыта известно, что эффективность работы продавцов в различных торговых точках неодинакова. Коммерческий директор компании произел оценку деятельности каждого продавца в  каждой торговой точке. Результаты этой оценки представлены в таблице.

Продавец	Объёмы продаж по торговым точкам, USD/тыс.шт.
I	II	III	IV	V	VI
A	68	72	75	83	75	69
B	56	60	58	63	61	59
C	35	38	40	45	25	27
D	40	42	47	45	53	36
E	62	70	68	67	69	70

Решение: