ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Филиал в г. Барнауле

Кафедра математики и информатики

ОТЧЕТ

О результатах выполнения

компьютерной лабораторной работы

Вариант № 3

                                                                    Выполнила:

Барнаул 2007 г

ОТЧЕТ О ВЫПОЛНЕНИИ ЛАБОРАТОРНОЙ РАБОТЫ

ЗАДАЧА №1

Вариант №3

Металлургическому заводу требуется уголь с содержанием фосфора не более 0,03% и с долей зольных примесей не более 3,25%. Завод закупает три сорта угля - А, В, С с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты А, В, С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену? Содержание примесей и цена исходных продуктов приведены в таблице.

Сорт угля	Содержание (%)	Цена 1 т (руб.)
фосфора	золы
А	0,06	2,0	30
В	0,04	4,0	30
С	0,02	3,0	45

Решение

 

1.      Перечислить искомые переменные и указать их смысл.

X1- доля сорта угля А, в %

Х2 - доля сорта угля В, в %

Х3 - доля сорта угля С, в %

Ограничения задачи имеют вид:

min (30x1+30x2+45x3

0,06x1+0,04x2+0,02x3≤0,03

2,0x1+4x2+3x3≤3,25

x1+x2+x3=1

x1,x2,x3≥0

Перенесем параметры задачи в ячейки следующим образом

Введем исходные данные задачи

x1	x2	x3
30	30	45
0,06	0,04	0,02		0,03
2	4	3		3,25
1	1	1		1
1				0
	1			0
		1		0

Поместим курсор в ячейку Е22, произойдет выделение ячейки

Поместим курсор на кнопку Мастер функций, расположенной на панели инструментов.

В окне Категория выберем Математические

В окне Функции выберем строку СУММПРОИЗВ

В строку Массив 1 введем В21: D21

В строку Массив 2 введем В22: D22

               

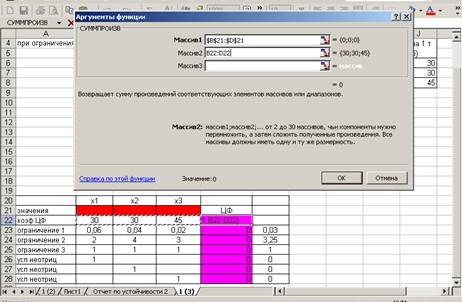
Поместим курсор в ячейку Е22

На панели инструментов кнопка Копировать в буфер

Поместим курсор в ячейку Е23

На панели инструментов найдем Вставить из буфера

Аналогично вставляем во все ограничения

В строке Меню указатель мышки поместим на Сервис. в развернутом меню выберем команду Поиск решения. запустим команду поиск решения

Поместим курсор в строку Установить целевую ячейку

Введем адрес ячейки

Ведем тип целевой функции.

Поместим курсор в строку Изменяя ячейки.

Введем адреса искомых переменных

Поместим указатель мыши на кнопку добавить

Добавим ограничения

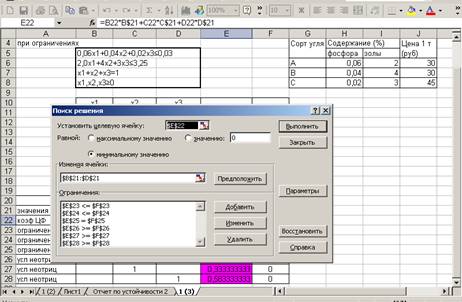
В диалоговом окне поместим указатель мышки на кнопку Параметры.

Установим флажки в окнах Линейная модель и Неотрицательные значения

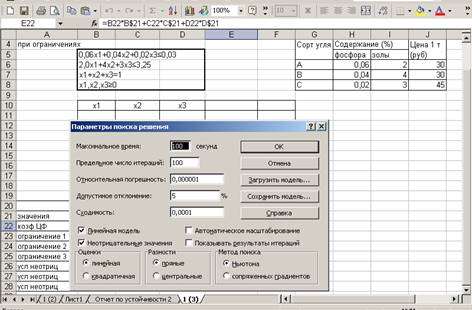
Поместим указатель мышки на кнопку ОК.

Помесим указатель мышки на кнопку Выполнить.

Сохранить найденное решение

	x1	x2	x3
значения	0,083333	0,33333333	0,58333333	ЦФ
коэф ЦФ	30	30	45	38,75
ограничение 1	0,06	0,04	0,02	0,03	0,03
ограничение 2	2	4	3	3,25	3,25
ограничение 3	1	1	1	1	1
усл неотриц	1			0,083333333	0
усл неотриц		1		0,333333333	0
усл неотриц			1	0,583333333	0

Укажем тип отчета Устойчивость, получим дополнительную информацию об оптимальном решении

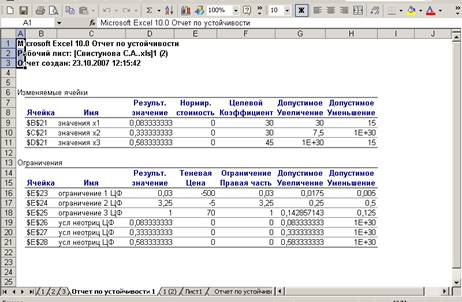
В результате решения задачи был получен ответ: необходимо в данной пропорции(0,83; 0,33; 0,58) смешивать сходные продукты А, В, С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену 38,75 руб.

                                                                      ЗАДАЧА №2

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на 5 участках автодорог. Песок на  участки ремонтных работ может доставляться из 3 карьеров, месячные объемы предложений по карьерам  известны. Из планов производства ремонтных работ известно месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат ( в у.е.) на перевозку одной тонны песку с карьеров на ремонтные участки.

Числовые данные для решения содержаться ниже в матрице планирования

Карьер	Участок работ	Предложение
В1	В2	В3	В4	В5
А1	4	2	3	4	1	60
А2	2	4	3	5	6	90
А3	6	5	4	6	2	140
Потребности	40	30	90	80	50

Требуется :

1. Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.

2. Определить, что произойдет с  оптимальным планом, если изменятся условия перевозок: а) появиться запрет на перевозки от первого карьера до второго участка работ; б) по этой коммуникации будет ограничен объем перевозок трем тоннам.  

 

 

Решение

 

2. Перечислить искомые переменные и указать их смысл.

 

Х1-  это объем потребностей по первому участку ( В1)

Х2- это объем потребности по второму участку    ( В2)

Х3- это объем потребности по третьему участку   (В3)

Х4- это объем потребности по четвертому участку ( В4)

Х5- это объем потребности по пятому участку        ( В5)                      

Хij- это оптимальный план.   

3 .Записать математическую модель задачи, указать смысл целевой функции и ограничений.

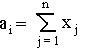
где а_i - мощность поставщика i;

Xij- Объем поставки песка от карьера I на ремонтные участки j
n- количество ремонтных участков

	Матрица планирования
5	1	1	1	1	1
5	1	1	1	1	1
5	1	1	1	1	1
	3	3	3	3	3

Исходные данные
	40	30	90	80	50
60	4	2	3	4	1
90	2	4	3	5	6
140	6	5	4	6	2

Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза, необходимо зарезервировать ячейку и ввести формулу для ее вычисления

       ^{n  m}

F=SS   c_ijx_ij

     _y=1i=1

где c_ij – стоимость доставки единицы груза от поставщика i  к потребителю j

x_ij – объем поставки груза от поставщика i к потребителю j

Для этого необходимо произвести следующие действия:

Поместить курсор в ячейку В25

Запустим Мастер функций

В окне Категория выберем Математические

В окне Функция при помощи спинера выберем СУММПРОИЗВ

Нажмем кнопку ОК

В окне СУММПРОИЗВ укажем адреса массивов, элементы которых обрабатываются этой функцией

В поле Массив 1 укажем адреса В3:F5

В поле Массив 2 укажем адреса В19:F21

min

970

Выберем Сервис=>Поиск решений

Поместим курсор в поле Установить целевую ячейку

Введем адрес$B$25

Установим направление изменения целевой функции, равное Минимальному значению

Вводим адреса измененных ячеек В19:F21.Для этого необходимо:

Выбрать Изменяя ячейки

Вводим адреса $B$19:$F$21

Выберем Добавить ограничения

В поле Ссылка на ячейку вводим адреса $G$19:$G$21

В среднем поле устанавливаем знак «=»

В поле Ограничение устанавливаем адреса $A$3:$A$5

Для подтверждения введенного условия нажимаем кнопку ОК

Выбираем Добавить ограничения

В поле Ссылка на ячейку вводим адрес $B$22:$F$22

В поле знака выбираем знак равенства

В поле Ограничения установим адрес $B$2:$F$2

Нажимаем кнопку ОК

После этого возвращаемся в поле Поиск решения. После ввода всех ограничений нажимаем ОК. На экране появится окно Поиск решения с введенными ограничениями

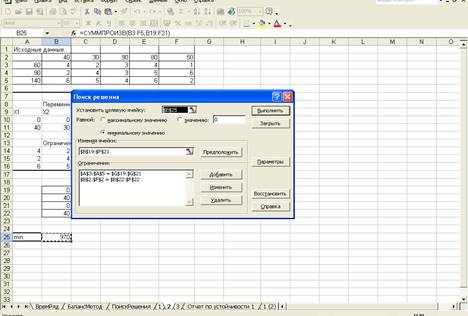
Щелкнем по кнопке Параметры

Выбираем переключатель Линейная модель и Неотрицательные значения

Нажимаем кнопку ОК. После этого произойдет переход в поиск решения

Нажимаем кнопку Выполнить.

	Матрица перевозок (изменяемые ячейки)
0	30	0	30	0	60
40	0	50	0	0	90
0	0	40	50	50	140
40	30	90	80	50

Отчет по устойчивости задачи