СОДЕРЖАНИЕ

Исходные данные.

Задание 1. Регрессионно-корреляционный                                                                                                                                                                                                                                                                                                                                                                                                                                                       анализ.

Задание 2. Факторный анализ.


Задание 3. Компонентный анализ.

Задание 4. Дискриминаторный анализ и оптимальная группировка объектов.

Исходные данные:

Номер

объекта

Индекс

динамики

себестои-мости

продукции, Y2%

Трудо-емкость

единицы

продук-

ции,

X1 чел./изд.

Удельный

вес

рабочих

в составе

персонала, X2

Удельный вес покупных

изделий в общих затратах

На производство, X3

Премии и

вознагра-ждения

на 1 работника,

 X5 тыс.руб.

1

204,2

0,23

0,78

0,4

1,23

2

209,6

0,24

0,75

0,26

1,04

3

222,6

0,19

0,68

0,4

1,8

4

236,7

0,17

0,7

0,5

0,43

5

62

0,23

0,62

0,4

0,88

6

53,1

0,43

0,76

0,19

0,57

7

172,1

0,31

0,73

0,25

1,72

8

56,5

0,26

0,71

0,44

1,7

9

52,6

0,49

0,69

0,17

0,84

10

46,6

0,36

0,73

0,39

0,6

11

53,2

0,37

0,68

0,33

0,82

12

30,1

0,43

0,74

0,25

0,84

13

146,4

0,35

0,66

0,32

0,67

14

18,1

0,38

0,72

0,02

1,04

15

13,6

0,42

0,68

0,06

0,66

16

89,8

0,3

0,77

0,15

0,86

17

62,5

0,32

0,78

0,08

0,79

18

46,3

0,25

0,78

0,2

0,34

19

103,5

0,31

0,81

0,2

1,6

20

73,3

0,26

0,79

0,3

1,46

 

Задание 1. Регрессионно-корреляционный анализ.

Уравнение регрессии ищем в виде:

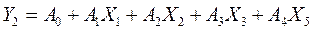
Используем автоматизированное вычисление множественного линейного уравнения связи (регрессии)  с помощью EXCEL.

Получаем уравнение множественной связи:

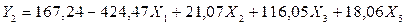
Из уравнения видно, что основным признаком, определяющим уровень снижения себестоимости продукции является повышение трудоемкости единицы продукции. Уменьшение трудоемкости единицы продукции на 1 чел./изд. увеличивает индекс себестоимости продукции на 424,47 процентных пункта.

Наиболее заметным признаком – фактором удорожания продукции является удельный вес покупных изделий в общих затратах на производство. Повышение доли этих затрат на один пункт (0,01) увеличивает индекс динамики себестоимости на 1,16%.

Значимость уравнения регрессии в целом оцениваем посредством F-критерия. По результатам дисперсионного анализа (посредством EXCEL, результаты на след. стр.)  имеем

.

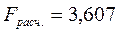По таблице для  уровня значимости a = 0,05, к1 = 4, к2 = 20 – 4 – 1 = 15 находим 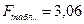. Так как 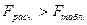, делаем вывод о значимости уравнения множественной регрессии.

Оценим тесноту связи признака-результата с признаками-регрессорами с помощью коэффициента множественной детерминации R2. По результатам регрессионной статистики R2 = 0,49 – это означает, что 49 % вариации результативного признака объясняется вариацией факторных переменных, т.е. полученное уравнение не достаточно хорошо описывает изучаемую взаимосвязь между факторами.

ВЫВОД ИТОГОВ















Регрессионная статистика






Множественный R

0,700223






R-квадрат

0,490312






Нормированный R-квадрат

0,354395






Стандартная ошибка

58,53297






Наблюдения

20















Дисперсионный анализ





 

df

SS

MS

F

Значимость F


Регрессия

4

49437,91

12359,48

3,607439

0,029839


Остаток

15

51391,63

3426,109




Итого

19

100829,5

 

 

 











 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

Y-пересечение

167,2374

267,1635

0,625974

0,540741

-402,208

736,6833

-402,208

736,6833

Переменная X 1

-424,471

206,3497

-2,05705

0,057506

-864,295

15,35344

-864,295

15,35344

Переменная X 2

21,07086

299,2958

0,070401

0,944804

-616,863

659,0051

-616,863

659,0051

Переменная X 3

116,0467

139,5348

0,831668

0,41864

-181,365

413,4583

-181,365

413,4583

Переменная X 4

18,06021

31,91179

0,565942

0,579802

-49,9582

86,07861

-49,9582

86,07861



























Проверим параметры уравнения регрессии на значимость с помощью t – критерия. Наблюдаемые значения t – критерия составляют:

t(A0) =

0,625974

t(A1) =

-2,05705

t(A2) =

0,070401

t(A3) =

0,831668

t(A4) =

0,565942


Для данной задачи табличное значение t – критерия равно 1,75 при вероятности его превышения (по абсолютному значению), равной 0,1. Так как ни одно из фактических значений t – критерия не превышает табличного, делаем вывод о случайности полученных величин Аj.


Следующий этап регрессионного анализа – исключение тех признаков-регрессоров, которые оказывают незначительное влияние на результативный показатель.

По результатам t – критерия самым незначительным является признак Х2. Удалив Х2,  получаем уравнение регрессии:

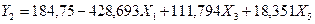
Наблюдаемые значения t – критерия составляют:

t(A0) =

1,955

t(A1) =

-2,242

t(A3) =

0,917

t(A5) =

0,599

при табличном уровне tкр=1,74 для  a/2 = 0,05 и n = 17. Делаем вывод о значимости параметров А0 и А1.

По результатам дисперсионного анализа имеем

.

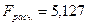Получено уменьшение F – критерия при незначительном снижении коэффициента множественной корреляции.


По результатам t – критерия самым незначительным является признак Х5. Удалив Х5,  получаем уравнение регрессии:

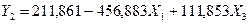
Наблюдаемые значения t – критерия составляют:


t(A0) =

2,605

t(A1) =

-2,513

t(A3) =

0,936

при табличном уровне tкр=1,74 для  a/2 = 0,05 и n = 17. Делаем вывод о значимости параметров А0 и А1.

По результатам дисперсионного анализа имеем

.

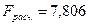Получено заметное увеличение F – критерия при незначительном снижении коэффициента множественной корреляции.


Продолжая процесс исключения и сравнивая результаты регрессионной статистики  для Y2, X1  и  Y2, X3 убеждаемся, что наилучшим оказывается уравнение парной регрессии

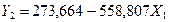
Основным признаком, определяющим уровень снижения себестоимости продукции является повышение трудоемкости единицы продукции. Уменьшение трудоемкости единицы продукции на 1 чел./изд. увеличивает индекс себестоимости продукции на 558,807 процентных пункта.




 

ВЫВОД ИТОГОВ















Регрессионная статистика для Y2, X1, X3,Х5





Множественный R

0,700102






R-квадрат

0,490143






Дисперсионный анализ





 

df

SS

MS

F

Значимость F


Регрессия

3

49420,93

16473,64

5,127123

0,011262











 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

Y-пересечение

184,7472

94,47717

1,95547

0,068224

-15,5354

385,0298

-15,5354

385,0298

Переменная X 1

-428,693

191,2038

-2,24207

0,03948

-834,027

-23,3592

-834,027

-23,3592

Переменная X 3

111,7943

121,8101

0,917775

0,372365

-146,432

370,0202

-146,432

370,0202

Переменная X 5

18,3506

30,64432

0,598825

0,557673

-46,6124

83,31364

-46,6124

83,31364

 

ВЫВОД ИТОГОВ















   Регрессионная статистика для Y2, X1, X3





Множественный R

0,691893






R-квадрат

0,478716






Дисперсионный анализ





 

df

SS

MS

F

Значимость F


Регрессия

2

48268,76

24134,38

7,805905

0,003937


Остаток

17

52560,78

3091,811




Итого

19

100829,5

 

 

 











 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

Y-пересечение

211,8613

81,34096

2,604608

0,018503

40,24662

383,4759

40,24662

383,4759

Переменная X 1

-456,883

181,7885

-2,51327

0,022333

-840,424

-73,3421

-840,424

-73,3421

Переменная X 3

111,8525

119,4901

0,936082

0,362339

-140,25

363,9548

-140,25

363,9548

 

ВЫВОД ИТОГОВ















Регрессионная статистика для Y2 и Х1






Множественный R

0,672196






R-квадрат

0,451847






Дисперсионный анализ





 

df

SS

MS

F

Значимость F


Регрессия

1

45559,57

45559,57

14,83757

0,001168











 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

Y-пересечение

273,6643

47,34742

5,77992

1,77E-05

174,191

373,1377

174,191

373,1377

Переменная X 1

-558,807

145,0711

-3,85196

0,001168

-863,591

-254,024

-863,591

-254,024

 

 

ВЫВОД ИТОГОВ















Регрессионная статистика для Y2 и Х3






Множественный R

0,533881






R-квадрат

0,285029






Дисперсионный анализ





 

df

SS

MS

F

Значимость F


Регрессия

1

28739,33

28739,33

7,175839

0,015326











 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

Y-пересечение

20,1866

32,19091

0,62709

0,538474

-47,444

87,81724

-47,444

87,81724

Переменная X 1

291,7266

108,9029

2,678776

0,015326

62,92979

520,5233

62,92979

520,5233

 Задание 2. Факторный анализ.

Используя анализ данных в EXCEL:

 

X1 

X2 

X3 

X5 





Среднее

0,315

0,728

0,2655

0,9945

Стандартная ошибка

0,019595

0,01123

0,029811

0,099566

Медиана

0,31

0,73

0,255

0,85

Мода

0,23

0,78

0,4

1,04

Стандартное отклонение

0,08763

0,050221

0,133317

0,445273

Дисперсия выборки

0,007679

0,002522

0,017773

0,198268

Эксцесс

-0,72114

-0,55808

-0,76502

-0,78293

Асимметричность

0,249508

-0,30395

-0,13229

0,594076

Интервал

0,32

0,19

0,48

1,46

Минимум

0,17

0,62

0,02

0,34

Максимум

0,49

0,81

0,5

1,8

Сумма

6,3

14,56

5,31

19,89

Счет

20

20

20

20

Находим матрицу исходных данных в стандартизированном виде:

-0,9700

1,0354

1,0089

0,5289

-0,8559

0,4381

-0,0413

0,1022

-1,4265

-0,9558

1,0089

1,8090

-1,6547

-0,5575

1,7590

-1,2678

-0,9700

-2,1505

1,0089

-0,2571

1,3123

0,6372

-0,5663

-0,9533

-0,0571

0,0398

-0,1163

1,6293

-0,6276

-0,3584

1,3089

1,5844

Z =

1,9970

-0,7567

-0,7163

-0,3470

0,5135

0,0398

0,9339

-0,8860

0,6276

-0,9558

0,4838

-0,3919

1,3123

0,2389

-0,1163

-0,3470

0,3994

-1,3540

0,4088

-0,7288

0,7418

-0,1593

-1,8415

0,1022

1,1982

-0,9558

-1,5414

-0,7512

-0,1712

0,8363

-0,8664

-0,3021

0,0571

1,0354

-1,3914

-0,4593

-0,7418

1,0354

-0,4913

-1,4699

-0,0571

1,6328

-0,4913

1,3598

-0,6276

1,2345

0,2588

1,0454

Используя автоматизированное вычисление  с помощью EXCEL, получаем матрицу R:

X1

X2

X3

X5

X1

1,000

-0,066

-0,599

-0,303

X2

-0,066

1,000

-0,304

0,131

X3

-0,599

-0,304

1,000

0,182

X5

-0,303

0,131

0,182

1,000

Зададим показатели общности по правилу 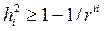, где - элемент главной диагонали матрицы R-1. С помощью EXCEL получаем R-1:

1,814

0,438

1,169

0,279

0,438

1,253

0,672

-0,154

1,169

0,672

1,919

-0,083

0,279

-0,154

-0,083

1,120

Тогда ,   ,   ,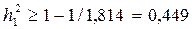  

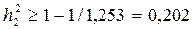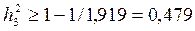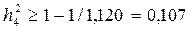
Матрица Rh получается из R заменой единиц на главной диагонали показателями общности, полученных методом максимальных элементов строк матрицы R:

X1

X2

X3

X5

X1

0,449

-0,066

-0,599

-0,303

X2

-0,066

0,202

-0,304

0,131

X3

-0,599

-0,304

0,479

0,182

X5

-0,303

0,131

0,182

0,107

Находим собственный вектор и собственное число матрицы Rh по матрице Rh, проведя необходимое число итераций, достигнув точности 0,001 (это легко делается в EXCEL):

a0

b1

a1

b2

a2

b3

a3

b4

a4

b5

a5

b6

a6

1

-0,5190

-1,0000

-0,2333

-0,5322

-1,0325

-1,0000

-1,0091

-0,9583

-1,1574

-0,9923

-1,1645

-0,9660

1

-0,0370

-0,0713

0,2229

0,5085

-0,0966

-0,0935

-0,1115

-0,1059

-0,2037

-0,1747

-0,2169

-0,1800

1

-0,2420

-0,4663

0,4384

1,0000

0,7399

0,7166

1,0530

1,0000

1,1664

1,0000

1,2055

1,0000

1

0,1170

0,2254

0,2329

0,5314

0,4667

0,4520

0,4695

0,4459

0,5062

0,4340

0,5062

0,4199

 

0,5190

 

0,4384

 

1,0325

 

1,0530

 

1,1664

 

1,2055

 

b7

a7

b8

a8

b9

a9

b10

a10

b11

a11

b12

a12

-1,1481

-0,9658

-1,1468

-0,9636

-1,1453

-0,9633

-1,1450

-0,9631

-1,1448

-0,9630

-1,1448

-0,9630

-0,2216

-0,1864

-0,2232

-0,1876

-0,2238

-0,1883

-0,2240

-0,1884

-0,2241

-0,1885

-0,2241

-0,1885

1,1888

1,0000

1,1901

1,0000

1,1889

1,0000

1,1889

1,0000

1,1887

1,0000

1,1887

1,0000

0,4961

0,4173

0,4949

0,4158

0,4939

0,4154

0,4937

0,4152

0,4936

0,4152

0,4935

0,4152

1,1888

 

1,1901

 

1,1889

 

1,1889

 

1,1887

 

1,1887

 

Первый собственный вектор матрицы Rh :

-0,963

а(1) = 

-0,189

1,000

0,415

Первое собственное число матрицы Rh   l1 =.1,189

Тогда


-0,7834

А1 =

-0,1534

0,8135

0,3377

 

Первичными признаками, наиболее коррелированными с первым фактором, оказываются Х1 и Х3.


Матрица воспроизведенных корреляций: R1 = A1 A1 Т

0,6137

0,1202

-0,6373

-0,2646

R1 =

0,1202

0,0235

-0,1248

-0,0518

-0,6373

-0,1248

0,6618

0,2747

-0,2646

-0,0518

0,2747

0,1141

 

Матрица остаточных корреляций: Rh - R1 :

-0,1647

-0,1862

0,0383

-0,0384

-0,1862

0,1785

-0,1792

0,1828

0,0383

-0,1792

-0,1828

-0,0927

-0,0384

0,1828

-0,0927

-0,0071

 

Так как на главной диагонали есть отрицательные элементы, то процесс выделения факторов при данных общностях  закончен.


Повторим процесс, задав новые общности как максимальные элементы строк.

Матрица Rh получается из R заменой единиц на главной диагонали показателями общности, полученных методом максимальных элементов строк матрицы R:

X1

X2

X3

X5

X1

0,599

-0,066

-0,599

-0,303

X2

-0,066

0,304

-0,304

0,131

X3

-0,599

-0,304

0,599

0,182

X5

-0,303

0,131

0,182

0,303

Находим собственный вектор и собственное число матрицы Rh по матрице Rh, проведя необходимое число итераций, достигнув точности 0,001 (это легко делается в EXCEL):

a0

b1

a1

b2

a2

b3

a3

b4

a4

b5

a5

b6

a6

1

-0,3502

-1,0000

-0,5413

-1,0000

-1,2238

-1,0000

-1,1646

-1,0000

-1,2244

-1,0000

-1,2397

-0,9983

1

0,0615

0,1757

0,2734

0,5051

0,0628

0,0513

-0,0923

-0,0793

-0,1761

-0,1438

-0,2102

-0,1692

1

-0,1159

-0,3310

0,4198

0,7756

0,9737

0,7957

1,0908

0,9367

1,2014

0,9812

1,2418

1,0000

1

0,1822

0,5202

0,3422

0,6322

0,5938

0,4852

0,5156

0,4427

0,5164

0,4217

0,5125

0,4127

0,3502

0,5413

1,2238

1,1646

1,2244

1,2418

b7

a7

b8

a8

b9

a9

b10

a10

b11

a11

b12

a12

-1,2452

-0,9904

-1,2382

-0,9872

-1,2355

-0,9860

-1,2344

-0,9855

-1,2339

-0,9853

-1,2337

-0,9852

-0,2242

-0,1783

-0,2281

-0,1819

-0,2296

-0,1833

-0,2303

-0,1838

-0,2305

-0,1841

-0,2306

-0,1842

1,2573

1,0000

1,2543

1,0000

1,2530

1,0000

1,2525

1,0000

1,2523

1,0000

1,2523

1,0000

0,5105

0,4060

0,5060

0,4034

0,5042

0,4023

0,5034

0,4019

0,5031

0,4018

0,5030

0,4017

1,2573

1,2543

1,2530

1,2525

1,2523

1,2523

Первый собственный вектор матрицы Rh :

-0,985

а(1) = 

-0,184

1,000

0,402

Первое собственное число матрицы Rh   l1 =.1,252

Тогда


-0,8383

А1 =

-0,1567

0,8509

0,3418

 

Первичными признаками, наиболее коррелированными с первым фактором, оказываются Х1 и Х3.


Матрица воспроизведенных корреляций: R1 = A1 A1 Т

 

0,7027

0,1314

-0,7133

-0,2865

R1 =

0,1314

0,0246

-0,1334

-0,0536

-0,7133

-0,1334

0,7240

0,2908

-0,2865

-0,0536

0,2908

0,1168

 


Матрица остаточных корреляций: Rh - R1 :

-0,1337

-0,1939

0,1442

-0,0013

-0,1939

0,2643

-0,1555

0,1776

0,1443

-0,1555

-0,1550

-0,1179

-0,0012

0,1776

-0,1179

0,0561

 

Анализируя матрицу остаточных корреляций, замечаем, что первый выделенный фактор объясняет вариацию первого и третьего исходных признаков более, нежели это предусматривалось при задании общностей.. Так как на главной диагонали есть отрицательные элементы, то процесс выделения факторов при данных общностях  закончен.

Распределение дисперсий:

Переменная

Х1

Общность

h12

Cпецифичность

b12

Характерность

u12 = 1- h12 - b12

1

0,5690

-

0,431

2

0,2889

0,264

0,447

3

0,5690

-

0,431

4

0,1729

0,0561

0,771

Первый выделенный фактор имеет реальное содержание, т.к. охватывает около 31% общей дисперсии (l1/4=1,2522/4=0,313). Первичными признаками, наиболее коррелированными с первым фактором являются Х2 и Х4.

Оценим уровни факторов на основе соотношения FT = AT R-1 ZT, где

-0,8383

А =

-0,1567

0,8509

0,3418

Получаем матрицу индивидуальных значений факторов по каждому объекту:


F1

1,0157

0,3964

1,4636

1,6359

1,0790

-1,0751

0,1323

1,1711

-1,3703

F =

0,1370

-0,0587

-0,7615

-0,0002

-1,3097

-1,4327

-0,4332

-0,8450

-0,0815

-0,1618

0,4987

                                     

Рассчитаем корреляцию между Y2, F1  c помощью EXCEL (результаты на след. стр.).

Наблюдается заметная корреляция между Y2 и F1.

Уравнение регрессии: .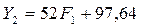

Критерий F=15,32 больше табличного (Fтабл.= 8,4 для a=0,01), поэтому уравнение регрессии можно считать статистически значимым с доверительной вероятностью не менее 0,99.

Сформируем уровни индивидуальных значений фактора F1 через первичные признаки. Матрица

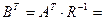
-0,4991

-0,0450

0,5197

0,1019

Получаем:

.

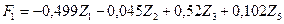Наибольшее влияние на индекс динамики себестоимости продукции проявляется через показатели Х1 и Х3.


ВЫВОД ИТОГОВ















Регрессионная статистика для Y2 и F1






Множественный R

0,678093






R-квадрат

0,459811






Нормированный R-квадрат

0,4298






Стандартная ошибка

55,0086






Наблюдения

20















Дисперсионный анализ





 

df

SS

MS

F

Значимость F


Регрессия

1

46362,51

46362,51

15,32166

0,001017


Остаток

18

54467,04

3025,947




Итого

19

100829,5

 

 

 











 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

Y-пересечение

97,64

12,3003

7,938019

2,74E-07

71,79801

123,482

71,79801

123,482

Переменная F1

51,99828

13,28422

3,914289

0,001017

24,08914

79,90742

24,08914

79,90742


Задание 3. Компонентный анализ.

Для решения задачи компонентного анализа используем метод главных компонент.

Для выделения первой компоненты определяем первый собственный вектор и соответствующее ему собственное число матрицы R коэффициентов корреляции первичных признаков Х:

1,000

-0,066

-0,599

-0,303

-0,066

1,000

-0,304

0,131

-0,599

-0,304

1,000

0,182

-0,303

0,131

0,182

1,000

 

Находим собственный вектор и собственное число матрицы R. Первый собственный вектор матрицы R:

-0,9961

а(1) = 

-0,2088

1,0000

0,5941

Первое собственное число матрицы R:   l1 =.1,768.

Тогда для первой компоненты получаем:

-0,64447

-0,8570

С1 =

-0,13511

 

А1 =

-0,1797

0,647013

0,8604

0,384416

0,5112

Матрица воспроизведенных корреляций: R1 = A1 A1 Т

0,7344

0,1540

-0,7373

-0,4381

R1 =

0,1540

0,0323

-0,1546

-0,0918

-0,7373

-0,1546

0,7402

0,4398

-0,4381

-0,0918

0,4398

0,2613

Матрица остаточных корреляций: R1 = R - R1 :

0,2656

-0,2200

0,1383

0,1351

-0,2200

0,9677

-0,1494

0,2228

0,1383

-0,1494

0,2598

-0,2578

0,1351

0,2228

-0,2578

0,7387

Находим собственный вектор и собственное число матрицы R1. Собственный вектор матрицы R1:

-0,1979

а(2) = 

1,0000

-0,3571

0,6207

Собственное число матрицы R1:   l2 =.1,203

Тогда для второй компоненты получаем:

-0,1589

-0,1743

С2 =

0,80271

 

А2 =

0,8804

-0,2867

-0,3144

0,49824

0,5464

Третья компонента дисперсии системы определяется по матрице остаточной корреляции, объясняемой только третьей и четвертой компонентами

 R’’ =R - (A1, A2) (А1,А2)Т

 

0,2352

-0,0665

0,0836

0,2303

R’’ =

-0,0665

0,1926

0,1274

-0,2582

0,0836

0,1274

0,1609

-0,0860

0,2303

-0,2582

-0,0860

0,4401

Находим собственный вектор и собственное число матрицы R''. Собственный вектор матрицы R’’:

0,5109

а(2) = 

-0,5942

-0,2095

1,0000

Собственное число матрицы R’’:   l3 =.0,729

Тогда для третьей компоненты получаем:

0,39676

0,3388

С3 =

-0,4615

 

А3 =

-0,3941

-0,1627

-0,1389

0,77664

0,6632

Аналогично определяем нагрузку четвертой компоненты.

0,1204

0,0670

0,1306

0,0056

R’’' =

0,0670

0,0373

0,0727

0,0032

0,1306

0,0727

0,1416

0,0061

0,0056

0,0032

0,0061

0,0003

Четвертый  собственный вектор матрицы R:

0,9222

а(4) = 

0,5132

1,0000

0,0430

Собственное число:   l4 =.0,3

Тогда для четвертой компоненты получаем:

0,63403

0,3470

С4 =

0,35281

 

А4 =

0,1931

0,6875

0,3763

0,02956

0,0162

Получаем матрицу С собственных векторов, последовательность собственных чисел и матрицу А – нагрузок компонент:

-0,64447

-0,1589

0,39676

0,63403

С =

-0,13511

0,80271

-0,4615

0,35281

0,647013

-0,2867

-0,1627

0,6875

0,384416

0,49824

0,77664

0,02956

l1 =.1,768;   l2 =.1,203;  l3 =0,729;   l4 =.0,3.

-0,8570

-0,1743

0,3388

0,3470

А =

-0,1797

0,8804

-0,3941

0,1931

0,8604

-0,3144

-0,1389

0,3763

0,5112

0,5464

0,6632

0,0162

Основная доля дисперсии приходится на 1-ю и 2-ю компоненты.

Найдем матрицу F =CT*Z (в матрицу С включаем первые два главных фактора):

F1

F2

1,3413

0,9595

0,5050

0,5504

2,3966

0,0715

1,7924

-1,3206

1,4696

-1,9895

-1,6647

-0,0097

0,5825

0,8862

1,9089

0,2262

-1,7817

-0,8922

-0,0727

-0,7588

-0,1130

-1,2009

-1,0867

-0,1563

-0,0901

-1,6307

-1,6087

0,3331

-1,9292

-0,8900

-0,6793

0,7964

-1,2535

0,9922

-0,5448

0,3575

0,0210

2,1381

0,8070

1,5374

Проводим анализ зависимости между Y2, F1 и F2.

Наблюдается заметная попарная корреляция между Y2, F1. Коэффициент множественной корреляции 0,681 достаточно близок к 1, что говорит о существенной зависимости между Y2, F1 и F2.


Уравнение регрессии признака-результата  по главным компонентам имеет вид: .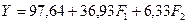

ВЫВОД ИТОГОВ















Регрессионная статистика для Y2, F1, F2






Множественный R

0,680803






R-квадрат

0,463492






Нормированный R-квадрат

0,400374






Стандартная ошибка

56,41017






Наблюдения

20















Дисперсионный анализ





 

df

SS

MS

F

Значимость F


Регрессия

2

46733,73

23366,87

7,343206

0,005028


Остаток

17

54095,81

3182,107




Итого

19

100829,5

 

 

 











 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

Y-пересечение

97,64

12,6137

7,740792

5,7E-07

71,02739

124,2526

71,02739

124,2526

Переменная F 1

36,92997

9,732099

3,794657

0,001448

16,39701

57,46293

16,39701

57,46293

Переменная F 2

6,331462

11,80111

0,536514

0,598555

-18,5667

31,22967

-18,5667

31,22967



























 

 

Столбец 1

Столбец 2

Столбец 3

 

 

Столбец Y2

1

 

 

Столбец F1

0,674098

1

 

 

Столбец F2

0,09517

-0,00021

1

 

Задание 4. Дискриминаторный анализ и оптимальная группировка объектов.

В качестве дискриминантных выберем признаки X1, X3, так как с ними при выделении первой главной компоненты и первого главного фактора связаны наибольшие факторные и компонентные нагрузки. Добавим также признак  X5.

Номер объекта

X1

X3

X5

1

0,23

0,4

1,23

2

0,24

0,26

1,04

3

0,19

0,4

1,8

4

0,17

0,5

0,43

5

0,23

0,4

0,88

6

0,43

0,19

0,57

7

0,31

0,25

1,72

8

0,26

0,44

1,7

9

0,49

0,17

0,84

10

0,36

0,39

0,6

11

0,37

0,33

0,82

12

0,43

0,25

0,84

13

0,35

0,32

0,67

14

0,38

0,02

1,04

15

0,42

0,06

0,66

16

0,3

0,15

0,86

17

0,32

0,08

0,79

18

0,25

0,2

0,34

19

0,31

0,2

1,6

20

0,26

0,3

1,46

Формируем первую обучающую выборку из объектов 1, 2, 3, имеющих минимальные значения 1 и 2 признаков. Во вторую обучающую выборку включаем объекты 9, 10,11, имеющих максимальные значения 1 и 2 признаков и проводим дискриминантный анализ с помощью STATISTICA:

Discriminant Function Analysis Summary (040306дискр)

No. of vars in model: 3; Grouping: тип (2 grps)

Wilks' Lambda: ,05672 approx. F (3,2)=11,086 p< ,0839

Wilks'

Partial

F-remove

p-level

Toler.

1-Toler.

X1

0,385608

0,147101

11,59610

0,076475

0,445067

0,554933

X3

0,101641

0,558075

1,58375

0,335226

0,471948

0,528052

X5

0,056932

0,996327

0,00737

0,939395

0,846771

0,153229

Изменим обучающие выборки. Формируем первую обучающую выборку из объектов 2, 3, 4. Во вторую обучающую выборку включаем объекты 9, 12,15 и проводим дискриминантный анализ:

Discriminant Function Analysis Summary (040306äèñêð)

No. of vars in model: 3; Grouping: òèï (2 grps)

Wilks' Lambda: ,05121 approx. F (3,2)=12,353 p< ,0758

Wilks'

Partial

F-remove

p-level

Toler.

1-Toler.

X1

0,328384

0,155931

10,82617

0,081268

0,792848

0,207152

X3

0,051662

0,991159

0,01784

0,905975

0,800074

0,199926

X5

0,055535

0,922034

0,16912

0,720776

0,942281

0,057719

Изменим обучающие выборки. Формируем первую обучающую выборку из объектов 7, 8, 19. Во вторую обучающую выборку включаем объекты 4, 10,18 и проводим дискриминантный анализ:

Discriminant Function Analysis Summary (040306äèñêð)

No. of vars in model: 3; Grouping: òèï (2 grps)

Wilks' Lambda: ,00205 approx. F (3,2)=325,12 p< ,0031

Wilks'

Partial

F-remove

p-level

Toler.

1-Toler.

X1

0,014129

0,144831

11,8092

0,075247

0,116609

0,883391

X3

0,013624

0,150195

11,3160

0,078151

0,131741

0,868259

X5

0,891119

0,002296

868,9418

0,001149

0,105125

0,894875

Минимальное из полученных значений статистики Уилкса равно 0,00205 (для третьей группировки) и близко к 0, что свидетельствует о хорошей дискриминации.

Первая обучающая выборка имеет вид:

Номер объекта

X1

X3

X5

7

0,31

0,25

1,72

8

0,26

0,44

1,7

19

0,31

0,2

1,6

Вектор средних значений по выборке 1:

0,2933

Х1 =

0,2967

1,6733

Вторая обучающая выборка имеет вид:

Номер объекта

X1

X3

X5

4

0,17

0,5

0,43

10

0,36

0,39

0,6

18

0,25

0,2

0,34

Вектор средних значений по выборке 2:

0,2600

Х2 =

0,3633

0,4567

Матрицы отклонений уровней признаков от средних:

0,0167

-0,0467

0,0467

U1 =

-0,0333

0,1433

0,0267

0,0167

-0,0967

-0,0733


-0,0900

0,1367

-0,0267

U2 =

0,1000

0,0267

0,1433

-0,0100

-0,1633

-0,1167

Матрицы внутривыборочных рассеиваний:

0,004641

-0,006

0,001372

U1 =

-0,006

0,022357

-0,01637

0,001372

-0,01637

0,015003


0,0275

-0,00918

-0,01831

U2 =

-0,00918

0,031248

-0,02208

-0,01831

-0,02208

0,040386

Объединенная матрица внутривыборочных  рассеиваний:

0,03214

-0,01518

-0,01694

U = U1 + U2

-0,01518

0,05360

-0,03845

-0,01694

-0,03845

0,05539



-136371,0

-136508,4

-136468,0

U-1 =

-136536,5

-136636,8

-136607,7

-136498,4

-136610,1

-136559,5

Определяем вектор разности средних значений признаков в выборках:

0,0333

(Х1 –  Х2) =

-0,0667

1,2167

Определяем вектор С дискриминантных множителей:

-161476,66

С = U-1(Х1 –  Х2) =        

-161643,579

-161585,447

Посредством дискриминантных множителей приводим массив исходных данных к одномерному представлению ( Z ):

X1

X3

X5

Z

1

0,23

0,4

1,23

-300547

2

0,24

0,26

1,04

-248831

3

0,19

0,4

1,8

-386192

4

0,17

0,5

0,43

-177755

5

0,23

0,4

0,88

-243992

6

0,43

0,19

0,57

-192251

7

0,31

0,25

1,72

-368396

8

0,26

0,44

1,7

-387802

9

0,49

0,17

0,84

-242335

10

0,36

0,39

0,6

-218124

11

0,37

0,33

0,82

-245589

12

0,43

0,25

0,84

-245578

13

0,35

0,32

0,67

-216505

14

0,38

0,02

1,04

-232643

15

0,42

0,06

0,66

-184165

16

0,3

0,15

0,86

-211653

17

0,32

0,08

0,79

-192257

18

0,25

0,2

0,34

-127637

19

0,31

0,2

1,6

-340923

20

0,26

0,3

1,46

-326392

Многомерная средняя первой обучающей выборки (объекты 7, 8, 19) равна

Z1 = -365497.

Многомерная средняя второй обучающей выборки (объекты 4, 10, 18) равна  Z2 = -174505,3.

Граница дискриминации:Z дискр.= (Z1 + Z2)/2 = -270001,17.

Итоги дискриминации:

Класс 1 – объекты 1,3,7,8,19,20.

Класс 2 – объекты 2,4,5,6,9,10,11,12,13,14,15,16,17,18.