Всероссийский заочный финансово-экономический институт
КОНТРОЛЬНАЯ РАБОТА
По дисциплине: «ФИНАНСОВАЯ
МАТЕМАТИКА»
Вариант № 9
Задание 1
ЗАДАЧА 1 (ИЗ КОНТГОЛЬНОЙ
РАБОТЫ)
Приведены поквартальные
данные о кредитах коммерческого банка, выданных на жилищное строительство (в
у.е.) за 4 года (всего 16 кварталов, первая строка соответствует первому
кварталу первого года).
Требуется:
1) Построить адаптивную мультипликативную
модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания
a1=0.3, a2=0.6, a3=0.3.
2) Оценить точность построенной модели,
вычислив среднюю относительную ошибку аппроксимации.
3) Проверить адекватность построенной
модели на основе исследования:
- случайности остаточной компоненты по
критерию числа точек поворота;
- независимости уровней ряда остатков по d-критерию (критические значения d1=1.10, d2=1.37) и по первому коэффициенту автокорреляции при
критическом значении r1=0.32;
- нормальности распределения остаточной
компоненты по R/S-критерию с критическими значениями 3 и 4.21.
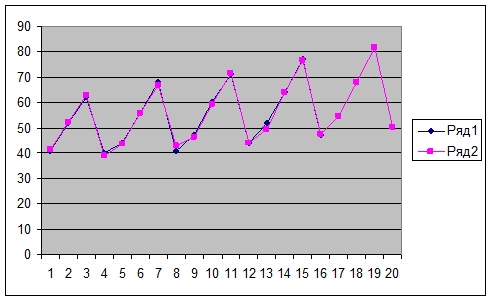
4) Отразить на графике фактические,
расчетные и прогнозные данные.
Вычисления провести в
среде EXCEL, точность – два знака после запятой.
Решение:
1. В столбец Y(t), строки 1-16 основной
таблицы внесем исходные данные.
Таблица 1
|
t
|
Y(t)
|
Yr(t)
|
a(t)
|
b(t)
|
F(t)
|
|
-3
|
|
|
|
|
|
|
-2
|
|
|
|
|
|
|
-1
|
|
|
|
|
|
|
0
|
|
|
|
|
|
|
1
|
41
|
|
|
|
|
|
2
|
52
|
|
|
|
|
|
3
|
62
|
|
|
|
|
|
4
|
40
|
|
|
|
|
|
5
|
44
|
|
|
|
|
|
6
|
56
|
|
|
|
|
|
7
|
68
|
|
|
|
|
|
8
|
41
|
|
|
|
|
|
9
|
47
|
|
|
|
|
|
10
|
60
|
|
|
|
|
|
11
|
71
|
|
|
|
|
|
12
|
44
|
|
|
|
|
|
13
|
52
|
|
|
|
|
|
14
|
64
|
|
|
|
|
|
15
|
77
|
|
|
|
|
|
16
|
47
|
|
|
|
|
|
17
|
|
|
|
|
|
|
18
|
|
|
|
|
|
|
19
|
|
|
|
|
|
|
20
|
|
|
|
|
|
2. Скопируемв столбец Y(t) таблицы 2
первые 8 значений из соответствующего столбца таблицы 1.
3. Во таблице 2 под столбцами t и
Y(t) вычислим средние значения (используя функцию СРЗНАЧ).
4. Провести вычисления в столбцах
t-tsr, Y-Ysr, (t-tsr)(Y(t)-Ysr), (t-tsr)*(t-tsr). Для этого
в соответствующие ячейки первой строки (при t=1) ввести соответствующие формулы,
при использовании ссылок на ячейки со значениями tsr, Ysr использовать абсолютную адресацию
(указаниям столбца и строки должен предшествовать знак $). Затем содержимое
этих ячеек скопируем в остальные ячейки того же столбца.
5. Под этими столбцами вычислим суммы
соответствующих значений.
- В
ячейки а(0), b(0) основной таблицы введем формулы
.
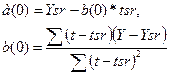- Во
вспомогательной таблице вычислим значения Yr1(t). Для этого в ячейку
Yr1(t) введем формулу =a(0)+t*b(0) (с абсолютными ссылками на
а(0), b(0)), затем
формулу скопируем в остальные ячейки столбца.
Таблица 2
|
t
|
Y(t)
|
Yr1(t)
|
t-tsr
|
Y-Ysr
|
(t-tsr)(Y(t)-Ysr)
|
(t-tsr)*(t-tsr)
|
|
1
|
41
|
47,75
|
-3,5
|
-9,5
|
33,25
|
12,25
|
|
2
|
52
|
48,54
|
-2,5
|
1,5
|
-3,75
|
6,25
|
|
3
|
62
|
49,32
|
-1,5
|
11,5
|
-17,25
|
2,25
|
|
4
|
40
|
50,11
|
-0,5
|
-10,5
|
5,25
|
0,25
|
|
5
|
44
|
50,898
|
0,5
|
-6,5
|
-3,25
|
0,25
|
|
6
|
56
|
51,68
|
1,5
|
5,5
|
8,25
|
2,25
|
|
7
|
68
|
52,46
|
2,5
|
17,5
|
43,75
|
6,25
|
|
8
|
41
|
53,25
|
3,5
|
-9,5
|
-33,25
|
12,25
|
|
4,5
|
50,5
|
|
0
|
0
|
33
|
42
|
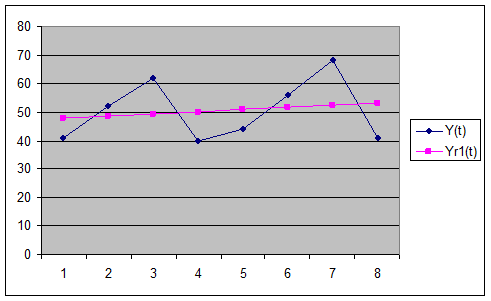
- Для
визуальной проверки полученных значений построим графики Y(t),
Yr1(t). Для этого активизируем в
меню «Вставка» позицию «Диаграмма/График», выберем во второй строке самую
левую позицию, затем следуем указаниям мастера диаграмм. В качестве данных
выберем первые два столбца второй таблицы.
9. Заполним таблицу 1. В ячейки F(-3), F(-2), F(-1), F(0) ввести нужные формулы (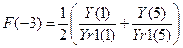
, в остальные ячейки формулу скопировать)
10.
Ввеем формулы в ячейки a(1) = a1 (Y(1)
/ F(-3) + (1- a1)*[a(0)+b(0)], b(1) = a3*
[a(1)-a(0)] + (1- a3)*b(0),
F(1) = a2 *Y(1)
/ a(1) + (1- a2)*F(-3),
Yr(1) = Yp(0+1) = [a(0)+1*b(0)]*F(0+1-4). При необходимости используем абсолютные ссылки (со знаком $).
Скопируем одновременно эти формулы в строки, соответствующие значениям t=2,…,16.
Таблица 1
|
t
|
Y(t)
|
Yr(t)
|
a(t)
|
b(t)
|
F(t)
|
|
-3
|
|
|
|
|
0,86
|
|
-2
|
|
|
|
|
1,08
|
|
-1
|
|
|
|
|
1,28
|
|
0
|
|
|
46,96
|
0,79
|
0,78
|
|
1
|
41
|
41,14
|
47,70
|
0,77
|
0,86
|
|
2
|
52
|
52,23
|
48,41
|
0,75
|
1,08
|
|
3
|
62
|
62,76
|
48,98
|
0,70
|
1,27
|
|
4
|
40
|
38,96
|
50,08
|
0,82
|
0,79
|
|
5
|
44
|
43,79
|
50,97
|
0,84
|
0,86
|
|
6
|
56
|
55,72
|
51,89
|
0,86
|
1,08
|
|
7
|
68
|
67,00
|
52,99
|
0,93
|
1,28
|
|
8
|
41
|
42,75
|
53,26
|
0,74
|
0,78
|
|
9
|
47
|
46,55
|
54,15
|
0,78
|
0,87
|
|
10
|
60
|
59,20
|
55,16
|
0,85
|
1,08
|
|
11
|
71
|
71,57
|
55,87
|
0,81
|
1,27
|
|
12
|
44
|
44,15
|
56,62
|
0,79
|
0,78
|
|
13
|
52
|
49,69
|
58,21
|
1,03
|
0,88
|
|
14
|
64
|
64,20
|
59,18
|
1,01
|
1,08
|
|
15
|
77
|
76,67
|
60,27
|
1,04
|
1,28
|
|
16
|
47
|
47,69
|
61,04
|
0,96
|
0,77
|
|
17
|
|
54,70
|
|
|
|
|
18
|
|
68,14
|
|
|
|
|
19
|
|
81,55
|
|
|
|
|
20
|
|
50,15
|
|
|
|
11.
Скопируем
значения столбцов Yr(1), Y(1) из основной таблицу в таблицу 3
(при копировании использовать режим «копировать только значения»).
12.
Аналогично
предыдущему, в первую строку таблицы 3 для вычисления значений E(t), отн.
погр., E(t)2 ввести формулы:
E(t) = Y(t) – Yr(t), отн. погр. = E(t) / Y(t), E(t)2 = E(t) * E(t). Скопируем эти формулы в остальные
ячейки столбца.
13.
Во
вторую строку таблицы 3 введем формулы для вычисления (E(2)-E(1))2, E(2)*E(1).
Скопируем эти формулы в остальные ячейки столбца.
14.
Во
вторую строку таблицы 3 введем формулу для проверки наличия точки поворота
(пример =ЕСЛИ(ИЛИ(И(E56<E57;E58<E57);И(E56>E57;E58>E57));1;0),
скопируем эту формулу в остальные ячейки столбца за исключением последней.
Таблица
3
|
t
|
Y(t)
|
Yr(t)
|
E(t)
|
отн. погр.
|
т. Поворота
|
E(t)2
|
(E(t)-E(t-1))
2
|
E(t)*E(t-1)
|
|
1
|
41
|
41,14
|
-0,14
|
-0,34
|
|
0,02
|
|
|
|
2
|
52
|
52,23
|
-0,23
|
-0,44
|
0
|
0,05
|
0,01
|
0,03
|
|
3
|
62
|
62,76
|
-0,76
|
-1,22
|
0
|
0,57
|
0,28
|
0,17
|
|
4
|
40
|
38,96
|
1,04
|
2,61
|
1
|
1,09
|
3,25
|
-0,79
|
|
5
|
44
|
43,79
|
0,21
|
0,48
|
1
|
0,04
|
0,70
|
0,22
|
|
6
|
56
|
55,72
|
0,28
|
0,49
|
0
|
0,08
|
0,00
|
0,06
|
|
7
|
68
|
67,00
|
1,00
|
1,47
|
1
|
1,00
|
0,52
|
0,28
|
|
8
|
41
|
42,75
|
-1,75
|
-4,28
|
1
|
3,08
|
7,58
|
-1,75
|
|
9
|
47
|
46,55
|
0,45
|
0,96
|
0
|
0,21
|
4,87
|
-0,79
|
|
10
|
60
|
59,20
|
0,80
|
1,33
|
1
|
0,63
|
0,12
|
0,36
|
|
11
|
71
|
71,57
|
-0,57
|
-0,81
|
1
|
0,33
|
1,88
|
-0,46
|
|
12
|
44
|
44,15
|
-0,15
|
-0,35
|
0
|
0,02
|
0,18
|
0,09
|
|
13
|
52
|
49,69
|
2,31
|
4,44
|
1
|
5,33
|
6,06
|
-0,36
|
|
14
|
64
|
64,20
|
-0,20
|
-0,32
|
1
|
0,04
|
6,30
|
-0,47
|
|
15
|
77
|
76,67
|
0,33
|
0,43
|
1
|
0,11
|
0,28
|
-0,07
|
|
16
|
47
|
47,69
|
-0,69
|
-1,47
|
|
0,48
|
1,04
|
-0,23
|
|
|
|
|
0,19
|
9
|
13,08
|
33,07
|
-3,71
|
15.
Вычислим
среднее значение величин из столбца отн. погр., сделаем вывод о точности
построенной модели. Условие точности выполнено, так как 0,19% < 5%.
16.
Вычислим
число точек поворота (сумма чисел в соответствующем столбце) p = 9, сравним с пороговым значением q> (2 * (N – 2)/ 3 – 2 * \| (16N – 29)/ 90 ), получаем q > 6. Так как р>q, условие случайности уровней ряда остатков выполнено.
17.
В какой-нибудь ячейке вычислим величину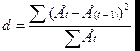 
= 2,5 сравним с
пороговыми (d2) и (d1), для нашего случая берем из таблицы d1=1.08 и d2=1.36. Т.к. d > 2,5, то используем d* = 4 - d = 4 – 2,5 =
1.5. Т.к. d* > d(1), но d* < d(2), то d-критерий не используется.
18.
В какой-нибудь ячейке вычислим статистическую
оценку первого коэффициента автокорреляции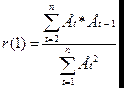 
= |0,28| ,
сравним с пороговым. Если |r(1)| < rтаб, то уровни ряда остатков независимы. Для нашей задачи
критический уровень rтаб = 0,32 - значит уровни независимы.
19.
В
какой-нибудь ячейке вычислить величину критерия
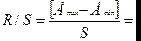4,35 , сравнить с пороговыми, которые зависят от точек
N и уровня
значимости. Для N =16 и 5 уровня значимости RS для нормального распределения находится от 3 до 4,21.
Полученное значение RS не попало в заданный интервал.
20.
Для
вычисления прогнозных значений в ячейку Yr(t), t=17 ввести формулу =(a(16)+(t-16)*b(16))*F(t-4)
с абсолютными ссылками на ячейки a(16), b(16)) и с относительной на ячейку t (время). Формулу скопировать в
ячейки t=18, 19, 20.
21.
Аналогично
п. 8 построим графики Y(t), Yr(t).
Задание 2
Даны цены (максимальная,
минимальная, закрытия) за 10 дней. Интервал сглаживания принять равным пяти
дням. Рассчитать:
- экспоненциальную
скользящую среднюю,
- момент,
- скорость изменения цен,
- индекс относительной
силы
- %R, %K, %D.
Расчеты проводить для
всех дней, для которых эти расчеты можно выполнить на основании имеющихся
данных.
Решение:
1. Сформируем таблицу исходных данных
|
Дни
|
Цены
|
|
Макс.
|
Мин.
|
Закр.
|
|
1
|
650
|
618
|
645
|
|
2
|
680
|
630
|
632
|
|
3
|
657
|
627
|
657
|
|
4
|
687
|
650
|
654
|
|
5
|
690
|
660
|
689
|
|
6
|
739
|
685
|
725
|
|
7
|
725
|
695
|
715
|
|
8
|
780
|
723
|
780
|
|
9
|
858
|
814
|
845
|
|
10
|
872
|
840
|
871
|
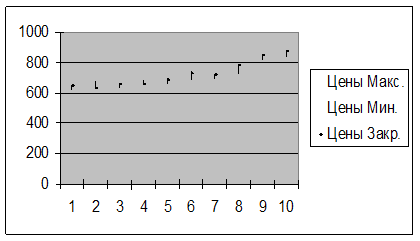
2. С помощью мастера диаграмм построим
гистограмму (штриховую диаграмму).
3. Для вычисления экспоненциальной
средней сформируем таблицу
|
Дни
|
Цены закр.
|
Эксп. Сред.
|
|
1
|
645
|
|
|
2
|
632
|
|
|
3
|
657
|
|
|
4
|
654
|
|
|
5
|
689
|
655,40
|
|
6
|
725
|
678,60
|
|
7
|
715
|
690,73
|
|
8
|
780
|
720,49
|
|
9
|
845
|
761,99
|
|
10
|
871
|
798,33
|
Вычисления проводем по формуле EMAi=k*Ci+(1-k)*EMAi-1. при i=6,…,10, n=5, k=2/(n+1)=1/3, значение EMA5 принимаем равным средней цене закрытия за 1-5 дни.
4. Аналогично п. 8 задачи 1 построим графики
цены закрытия и экспоненциальной средней(в одной системе координат.
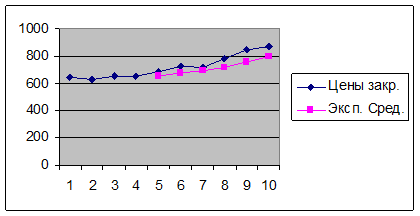
5. Для вычисления осцилляторов
сформируем таблицу
|
Дни
|
MOM
|
ROC
|
Пониж..
|
Повыш.
|
AU
|
AD
|
RSI
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
13
|
0
|
|
|
|
|
3
|
|
|
0
|
25
|
|
|
|
|
4
|
|
|
3
|
0
|
|
|
|
|
5
|
|
|
0
|
35
|
|
|
|
|
6
|
80
|
112,40
|
0
|
36
|
60
|
16
|
78,95
|
|
7
|
83
|
113,13
|
10
|
0
|
96
|
16
|
85,71
|
|
8
|
123
|
118,72
|
0
|
65
|
96
|
13
|
88,07
|
|
9
|
191
|
129,20
|
0
|
65
|
136
|
13
|
91,28
|
|
10
|
182
|
126,42
|
0
|
26
|
201
|
10
|
95,26
|
Вычисления проведем по формулам MOMi=Ci – Ci-5,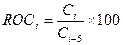 
(i=6,7,8,9,10), пониж. и повыш. (i=2,3,…,10) (вычислим с использованием функции ЕСЛИ, см.
п. 14 задачи 1).
6. Вычислим при i=6,…,10 введя в верхние ячейки и
копируя в остальные ячейки формулы AUi - суммы повыш. за предшествующие 5
дней, ADi - суммы пониж. за предшествующие 5 дней,), RSIi=100-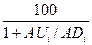
.
7. Построим графики МОМ, ROC, RCI.
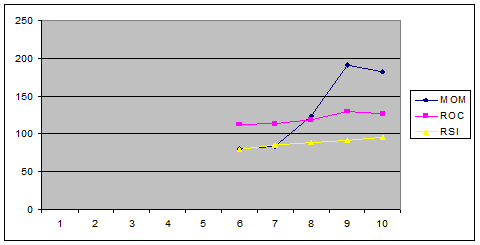
8. Для вычисления стохастических линий
сформировать таблицу
|
цена -
|
макс-мин
|
%K
|
%R
|
%D
|
|
71
|
72
|
98,61
|
1,39
|
-
|
|
98
|
112
|
87,50
|
12,50
|
-
|
|
88
|
112
|
78,57
|
21,43
|
86,82
|
|
130
|
130
|
100,00
|
0,00
|
89,26
|
|
185
|
198
|
93,43
|
6,57
|
91,59
|
Для вычисления значений минимальных и
максимальных цен за предшествующие дни используем функции МАКС и МИН. Вычисляем
по формулам
%K=100(цена
– мин)/ (макс-мин),
%R=100-%K (вычисления проводем при i=5,6,…,10),
%D
(вычисления проводем при i=7,8,9,10) равен отношению сумм цена – мин и макс-мин за три предшествующих
дня.
Задание 3.
Выполнить различные
коммерческие расчеты, используя данные, приведенные в таблице. В условии задачи
значения параметров приведены в виде переменных. Например, S означает некую сумму средств в
рублях, Тлет – время в годах, I – ставку в процентах и т.д. По
именам переменных из таблицы необходимо выбрать соответствующие численные
значения параметров и выполнить расчеты.
|
Вариант
|
Сумма
|
Дата
начальная
|
Дата
конечная
|
Время в днях
|
Время в годах
|
Ставка
|
Число начислений
|
|
S
|
T н
|
T k
|
T дн
|
T лет
|
i
|
m
|
|
9
|
4500000
|
09.01.02
|
21.03.02
|
90
|
5
|
50
|
4
|
3.1. Банк выдал ссуду, размером S рублей. Дата выдачи ссуды -
T н, возврата
- T
k. День выдачи и день возврата считается за один день.
Процента рассчитываются по простой процентной ставке i% годовых. Найти:
3.1.1 точные проценты с
точным числом дней ссуды;
3.1.2 обыкновенные
проценты с точным числом дней ссуды;
3.1.3 обыкновенные проценты с приближенным числом
дней ссуды.
Решение:
3.1.1 K
= 365, t = 71, I = S*i*t / K =
4500000*0,5*71 / 365 = 437671,23 руб.;
3.1.2 K
= 360, t = 71, I = S*i*t / K =
4500000*0,5*71 / 360 = 443750 руб.;
3.1.3 K
= 360, t = 71, I = S*i*t / K =
4500000*0,5*72 / 360 = 450000 руб.
3.2. Через T дн дней
после подписания договора должник уплатит S рублей. Кредит выдан под i% годовых (проценты обыкновенные).
Какова первоначальная сумма и дисконт?
Решение:
P = S / (1 +
T дн /
360 *i) = 4500000 / (1 + 90 / 360 *0,5)= 4000000 руб.;
D = S – P = 4500000
– 4000000 = 50000 руб.
3.3. Через T дн дней
предприятие должно получить по векселю S рублей. Банк приобрел этот вексель с
дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дням).
Определить полученную предприятием сумму и дисконт.
Решение:
D = S * d * T дн / 360 = 4500000 * 0,5 * 90 /360 = 562500
руб.;
P = S – D = 4500000 –
562500 = 3937500 руб.
3.4. В кредитном договоре на сумму S рублей и сроком на T лет лет,
зафиксирована ставка сложных процентов, равная i% годовых. Определить наращенную
сумму.
Решение:
Р = S * (1 + i)n = 4500000 * (1 + 0,5)5 = 34171875 руб.
3.5. Ссуда размером S рублей предоставлена на T лет. Проценты сложные, ставка - i% годовых. Проценты начисляются m раз в году. Вычислить наращенную
сумму.
Решение:
Р =
S * (1 + im / m)n*m = 4500000 * (1 + 0,5/4)5*4 = 47452922 руб,.
3.6. Вычислить эффективную ставку процента, если банк начисляет проценты m раз в году, номинальной ставки i% годовых.
Решение:
(1 + i э)n = (1 + im/ m) m*n
i э = (1 + i /
m)m - 1 = (1 + 0,5 / 4) 4 - 1 =0,6%.
3.7. Определить, какой должна быть
номинальная ставка при
начислении процентов m раз в году, чтобы обеспечить эффективную ставку i% годовых.
Решение:
(1 + i э)n = (1 + im / m) n*m
im =( m |/(1 + i э) – 1)*m = (4 |/(1 + 0,5) – 1)*4 = 0,43%.
3.8. Через T лет лет
предприятию будет выплачена сумма S рублей. Определить ее совместную
стоимость при условии, что применяется сложная процентная ставка i% годовых.
Решение:
S = Р * (1 + i )n
Р =
S / (1 + i )n = 4500000/(1 +
0,5) 5 = 592592,6 руб.
3.9. Через T лет лет по
векселю должна быть выплачена сумма S рублей. Банк учел вексель по
сложной учетной ставке i% годовых. Определить дисконт.
Решение:
d = i
Р =
S * (1 - i )n = 4500000*(1 -
0,5) 5 = 140625 руб.,
D = S – P = 4500000 –
140625 = 4359375 руб.
3.10. В течение T лет лет на расчетный счет в конце каждого года поступает по S рублей, на которые m раз в году начисляются проценты по
сложной годовой ставке i% годовых. Определить сумму на
расчетном счете к концу указанного срока.
Решение:
Р =
S * ((1 + i
э)n
– 1)/ i э= 4500000 * (1 + 0,6) 5– 1)/ 0,6 = 71143200 руб.