Индивидуальное задание по Эконометрике

Вариант 80

Имеются данные о потреблении дизельного топлива, объемах валовой продукции сельского хозяйства и общих объемах инвестиций (капитальных вложений) за 1985–2000 г.г. по одному из крупных экономических регионов, которые приведены в таблице 1. На основе имеющихся данных требуется решить следующие задачи.

Годы	Валовая продукция промышленности – x1 (млрд. р.)	Объем капитальных вложений – x2 (млрд. р.)	Объем потребления дизельного топлива – y (млн. т.)
1985	5,2	3,2	1,5
1986	6,3	3	1,1
1987	5,7	2,8	1,7
1988	5,8	2,6	1,3
1989	6,3	2,8	1,7
1990	6,6	3,2	1,9
1991	6,8	3,5	2,2
1992	7,3	4,1	2,1
1993	8	4,6	2,4
1994	8,4	4,8	2,8
1995	8,9	4,4	2,6
1996	8,6	4,2	2,2
1997	8,5	5	1,9
1998	8,9	4,8	3,2
1999	8,9	4,8	3
2000	8,8	5,1	2,8

Задача 1.

1.1. Выяснить, существует ли связь между потреблением дизельного топлива (y) и объемом валовой продукции (x₁). (Для этого построить поле рассеяния. На основе его визуального анализа выдвинуть гипотезу о виде статистической зависимости y от x₁). Найти точечные оценки неизвестных параметров модели. Выяснить, существует ли связь между потреблением дизельного топлива (y) и объемом капиталовложений (x₂). Найти оценки неизвестных параметров модели.

Решение.

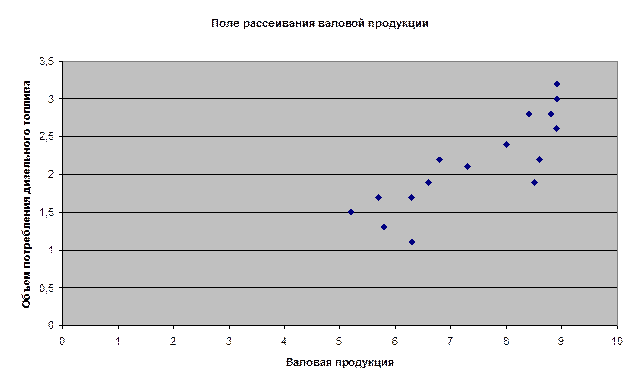
Рисунок 1.

На основе визуального анализа выдвигаем гипотезу о линейной зависимости y от x₁. Следовательно, зависимость y от x₁ описывается линейным уравнением y=a₀+a₁x₁.

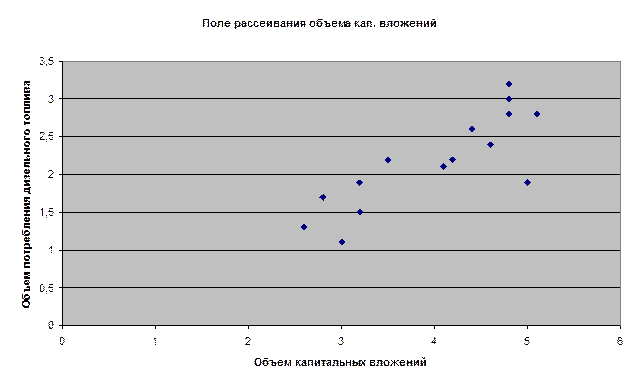
Рисунок 2.

На основе визуального анализа выдвигаем гипотезу о линейной зависимости y от x₂. Следовательно, зависимость y от x₂ описывается линейным уравнением y=b₀+b₁x₂.

Найдем коэффициенты зависимостей a₀, a₁, b₀, b₁ методом наименьших квадратов.

Для удобства вычисления искомых коэффициентов моделей составляется таблица:

№	x1	x2	y	x12	x22	x1y	x2y	x1x2	y2
1	5.2	3.2	1.5	27.04	10.24	7.8	4.8	16.64	2.25
2	6.3	3	1.1	39.69	9	6.93	3.3	18.9	1.21
3	5.7	2.8	1.7	32.49	7.84	9.69	4.76	15.96	2.89
4	5.8	2.6	1.3	33.64	6.76	7.54	3.38	15.08	1.69
5	6.3	2.8	1.7	39.69	7.84	10.71	4.76	17.64	2.89
6	6.6	3.2	1.9	43.56	10.24	12.54	6.08	21.12	3.61
7	6.8	3.5	2.2	46.24	12.25	14.96	7.7	23.8	4.84
8	7.3	4.1	2.1	53.29	16.81	15.33	8.61	29.93	4.41
9	8	4.6	2.4	64	21.16	19.2	11.04	36.8	5.76
10	8.4	4.8	2.8	70.56	23.04	23.52	13.44	40.32	7.84
11	8.9	4.4	2.6	79.21	19.36	23.14	11.44	39.16	6.76
12	8.6	4.2	2.2	73.96	17.64	18.92	9.24	36.12	4.84
13	8.5	5	1.9	72.25	25	16.15	9.5	42.5	3.61
14	8.9	4.8	3.2	79.21	23.04	28.48	15.36	42.72	10.24
15	8.9	4.8	3	79.21	23.04	26.7	14.4	42.72	9
16	8.8	5.1	2.8	77.44	26.01	24.64	14.28	44.88	7.84
Σ	119	62.9	34.4	911.48	259.27	266.25	142.09	484.29	79.68
сред.	7.44	3.93	2.15	56.97	16.2	16.64	8.88	30.27	4.98

По приведенным выше формулам получим:

a₀=2.15–0.3984·7.44=–0.814

Следовательно, получим приближенную зависимость

y=0.3984x₁–0.814

Аналогично получим:

a₀=2.15–0.57·3.93=–0.09

Следовательно, получим приближенную зависимость

y=0.57x₂–0.09

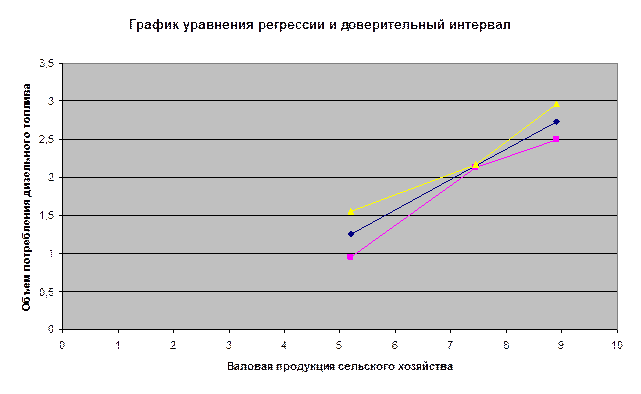
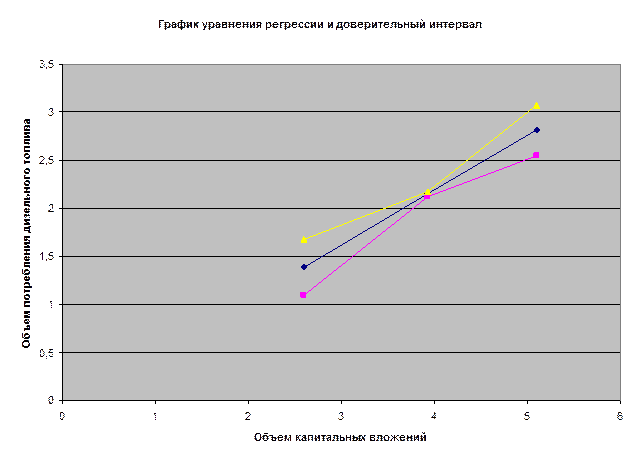
1.2. По найденным в п. 1.1. уравнениям регрессии построить доверительные интервалы потребления дизельного топлива, соответствующие вероятности 0.9, при следующих значениях независимой переменной: x=x_min, x=, x=x_max. Построить доверительную полосу для уравнения регрессии. Изобразить на графике поле рассеяния, прямые регрессии и доверительные полосы.

Решение.

Доверительные интервалы среднего потребления дизельного топлива для уравнения парной регрессии y=a₀+a₁x находятся по формуле:

 где y_в, y_н – соответственно верхняя и нижняя границы доверительного интервала; x₁^k – значение независимой переменной, для которой определяется доверительный интервал.

 – квантиль распределения Стьюдента (1–α) – доверительная вероятность, (n–2) – число степеней свободы.

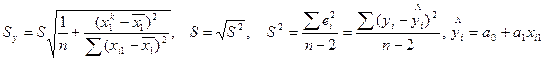
Пусть 1–α=0.9, тогда t_0.95,14 = 1.761

 1.2577

y₁=1.5;    e₁²=(1.5–1.2577)²=0.0587;

и т.д.

Подставив найденные значения в формулу для S², получим S²=0.1162; S=0.34.

Найдем значения .

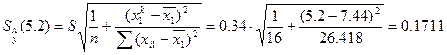
Аналогично находим

Внесем вычисленные данные в таблицу.

k	x1k
1	xmin=5.2	1.2577	0.1711	0.956	1.56
2		2.15	0.0129	2.127	2.173
3	xmax=8.9	2.7318	0.1291	2.5	2.96

Произведя аналогичные вычисления для второго уравнения, получим

k	x2k
1	xmin=2.6	1.392	0.1645	1.1	1.68
2		2.15	0.0153	2,123	2,177
3	xmax=5.1	2.817	0.1507	2.55	3.08

Задача 2.

2.1. Найти все коэффициенты парной корреляции, проверить их значимость и проанализировать тесноту линейной связи между всеми парами переменных.

Решение.

Коэффициент парной корреляции находится по формуле:

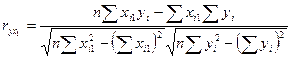
Подставив значения переменных, получим

Проверка существенности отличия r от нуля  производится по схеме: если 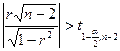, то гипотеза о существенном отличии коэффициента r от нуля принимается, а в противном случае – отвергается.

В данном случае.

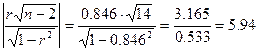
Аналогично получаем:

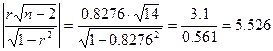
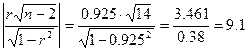
Следовательно, во всех трех случаях коэффициент корреляции сильно отличается от нуля и между всеми тремя парами переменных существует сильная линейная связь.

2.2. Найти по методу наименьших квадратов оценки коэффициентов линейной регрессионной модели .

Рассмотрим линейную регрессионную модель

По методу наименьших квадратов получим следующую систему уравнений.

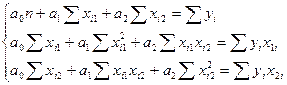
Подставив значения переменных, получим следующую систему уравнений:

Обозначим a=(a₀,a₁,a₂),

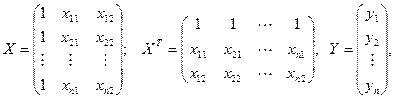
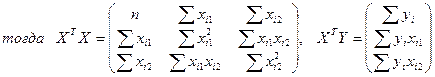
В данных обозначениях систему уравнений можно переписать следующим образом: (X^TX)a=X^TY , и, соответственно вектор а можно будет найти по формуле: a=(X^TX)^-1(X^TY).

Подставив исходные данные получим:

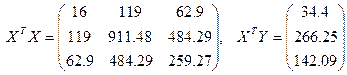
Определитель данной матрицы будет равен 728.95.

Обратная матрица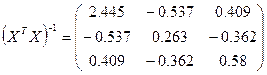

Соответственно находим вектор оценок a.

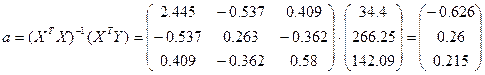
Таким образом, y=–0.626+0.26x₁+0.215x₂.

2.3. Найти коэффициенты множественной корреляции и детерминации.

Решение.

Коэффициент R множественной корреляции определяется по формуле:

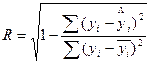
В нашем случае имеем

Коэффициент множественной детерминации R² равен квадрату коэффициента множественной корреляции. Следовательно, R²=0.73.

2.4. В 2005 году планируется увеличение объема валовой продукции на 1 млрд. руб. по сравнению с 2000 г., а объема капитальных вложений на 0,3 млрд. Дать точечный и интервальный прогноз среднего потребления топлива в 2005 году при уровне доверия 0.9. (Считая, что объемы валовой продукции и капитальных вложений в 2005 году будут равны запланированным.)

Решение.

Найдем параметры рассчитываемого прогноза.

Объем валовой продукции (параметр x₁), будет равен 8.8+1=9.8 млрд. руб.

Объем капитальных вложений (параметр x₂), будет равен 5.4 млрд. руб.

Под точечным прогнозом понимается значение ŷ=a₀+a₁x₁^p+a₂x₂^p, где x^p=(1, x₁^p, x₂^p) – вектор независимых переменных, для которого определяется прогноз. В нашем случае x^p=(1;9.8;5.4)

Исходя из этих данных получаем точечный прогноз:

y=–0.626+0.26·9.8+0.215·5.4=3.083

Найдем интервальный прогноз. Границы интервального прогноза можно определить по формуле:

ŷ_В,Н=ŷ(x^p)±, где y_в, y_н – соответственно верхняя и нижняя границы доверительного интервала; x^p – вектор независимых переменных, для которой определяется доверительный интервал.

 – квантиль распределения Стьюдента (1–α) – доверительная вероятность, (n–3) – число степеней свободы.

Пусть 1–α=0.9, тогда t_0.95,13 = 1.771

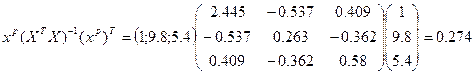
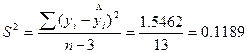
, тогда

ŷ_В,Н=3.083±1.771·0.18=3.083±0.319

ŷ_В =3.402

ŷ_Н=2.764

2.5. На основе полученных в задачах №№ 1,2 статистических характеристик провести содержательный экономический анализ зависимости потребления дизельного топлива от объемов валовой продукции сельского хозяйства и капитальных вложений.

Решение.

На основании проведенных расчетов и полученных статистических характеристик можно сделать определенные выводы относительно взаимосвязей между исследуемыми экономическими показателями. Рассмотрим вначале зависимость потребления дизельного топлива от объема валового выпуска продукции сельского хозяйства. Так как 0.846 и проверка значимости этого коэффициента показала существенное отличие от нуля, то есть основания утверждать, что между переменными y и x₁ существует достаточно тесная положительная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии y=0.3984x₁–0.814.

Коэффициент  a₀=–0.814 в данном случае не имеет экономического смысла, хотя формально определяет объем потребления дизельного топлива при x₁=0, т.е. при полном отсутствии сельскохозяйственного производства. А вот коэффициент a₁=0.3984  имеет вполне определенный экономический смысл, поскольку характеризует размер прироста потребления дизельного топлива, обусловленного приростом объема валового выпуска продукции сельского хозяйства на единицу, т.е. при увеличении объема производства валовой продукции сельского хозяйства на 1 млрд. рублей следует ожидать прироста потребления дизельного топлива в данном регионе на 0.3984 млн. тонн или на 398400 тонн.

Необходимо особо подчеркнуть, что слова «следует ожидать прироста потребления дизельного топлива…» в предыдущем предложении нельзя заменить словами «прирост потребления дизельного топлива составит…», так как уравнение регрессии у от х₁. Это уравнение характеризует так называемое среднее потребление дизельного топлива в зависимости от объема валового производства продукции сельского хозяйства. Слово «среднее» выражает здесь тот факт, что реальное значение объема потребления дизельного топлива у₁, соответствующее некоторому реальному объему валового выпуска х_i1, будет находиться в некоторой окрестности значения y_i=0.3984x_i1–0.814.

Значение  свидетельствует о том, что между у и х₂ существует достаточно тесная линейная зависимость. Экономический смысл коэффициента b₁=0.57 в уравнении y₂=0.57x₂–0.09 аналогичен смыслу коэффициента a₁=0.3984 в уравнении y_i=0.3984x_i1–0.814, т.е. b₁=0.57 показывает, какого прироста потребления дизельного топлива следует ожидать при увеличении объема капитальных вложений на единицу. Учитывая используемые единицы измерений переменных у и х₂, получаем, что при росте объема капитальных вложений на 1 млрд   руб. следует ожидать увеличения потребления дизельного топлива на  570000 тонн.

В результате исследования зависимости объема потребления дизельного топлива от двух факторов – объема валового выпуска продукции сельского хозяйства и объема капитальных вложений, получено уравнение множественной регрессии  y=–0.626+0.26x₁+0.215x₂.

Содержательный смысл найденных коэффициентов уравнения состоит в следующем. Величина a₁=0.26 показывает, что при росте валового выпуска продукции сельского хозяйства на 1 млрд.  руб. и фиксированном (неизменном) объеме капитальных вложений следует ожидать увеличения потребления дизельного топлива на 260 тыс. тонн. Коэффициент a₂=0.215 показывает, что при увеличении объема капитальных вложений на 1 млрд. руб. и неизменном объеме валовой продукции сельского хозяйства следует ожидать увеличения потребления дизельного топлива на  215 тыс.  тонн.

Сравнение результатов, полученных на основе анализа уравнений парной регрессии y_i=0.3984x_i1–0.814, y₂=0.57x₂–0.09 с результатами, полученными на основе анализа уравнения множественной регрессии y=–0.626+0.26x₁+0.215x₂, может создать представление об их противоречивости. Действительно, исследуя уравнения y_i=0.3984x_i1–0.814 и y₂=0.57x₂–0.09 были сделаны выводы о том, что ожидаемое увеличение потребления дизельного топлива составит:

·         398400 тонн при росте на 1 млрд. руб. валового выпуска сельскохозяйственной продукции;

·        570000 тонн при росте на 1 млрд. руб. объема капитальных вложений.

А исследование уравнения y=–0.626+0.26x₁+0.215x₂ показало, что ожидаемое увеличение потребления дизельного топлива составит:

·        260000 тонн при росте на 1 млрд. руб. валового выпуска продукции сельского хозяйства;

·        215000 тонн при росте на 1 млрд. руб. объема капитальных вложений.

На самом деле здесь нет никакого противоречия.

Действительно, исследуя зависимость  y=α₀+α₁x₁+u, мы исходим из того, что на объем потребления дизельного топлива влияет один единственный фактор – объем валового выпуска сельскохозяйственной продукции, а все остальные объясняющие факторы не учитывались (отбрасывались). Очевидно, что в реальной экономике на потребление дизельного топлива влияет множество факторов, и, в частности,

·        количество зарегистрированных в данном регионе транспортных средств и механизмов с дизельными двигателями;

·        объем розничного товарооборота в данном регионе;

·        объем реализации продукции теми предприятиями, которые занимаются оптовыми продажами, и т.д.

Поэтому, рассматривая модель y=α₀+α₁x₁+u, мы фактически объединили все влияющие на потребление дизельного топлива факторы в один результирующий и назвали этот фактор объемом валового выпуска продукции сельского хозяйства. Точно такое же объединение всех факторов в один результирующий фактор было осуществлено при рассмотрении модели y=β₀+β₁x₂+δ. Поэтому коэффициенты, отражающие степень (или силу) влияния каждого из двух рассмотренных факторов в отдельности на потребление дизельного топлива, оказались достаточно большими: a₁=0.3884;b₁=0.57.

Исследуя же модель y=α₀+α₁x₁+α₂x₂+u, мы рассмотрели совместное влияние двух факторов на потребление дизельного топлива, и это, естественно, привело к уменьшению значений коэффициентов, отражающих силу влияния каждого из этих факторов на результирующий показатель:

вместо a₁=0.3884 стало a₁=0.26;

вместо b₁=0.57 стало a₂=0.215.

Если рассмотреть модель вида y=α₀+α₁x₁+α₂x₂+α₃x₃+u, где х₃ – некоторый третий фактор, оказывающий положительное влияние на потребление дизельного топлива (т.е. увеличение х₃ приводит к увеличению у), и вычислить оценки неизвестных параметров α₀, α₁, α₂, α₃, т.е. получить уравнение регрессии y=α₀+α₁x₁+α₂x₂+α₃x₃+u, то коэффициенты α₁, α₂ этого уравнения скорее всего будут еще меньше, т.е. будут удовлетворять неравенствам α₁≤0.26; α₂≤0.215:

Проведенное рассуждение свидетельствует, в частности,  о том, что для более точного описания изменении исследуемого показателя следует включать в эконометрическую модель по возможности большее количество объясняющих переменных (факторов). Вместе с тем увеличение количества объясняющих факторов должно проводиться достаточно осторожно,  поскольку, с одной стороны, в числе этих факторов может оказаться такой, который на самом деле не оказывает сколько-нибудь существенное влияние на объясняемую  переменную у, а с другой стороны, математическая модель может оказаться слишком громоздкой и неудобной для анализа. Существуют различные методы выявления и отбора существенных факторов. Простейший основан на вычислении и анализе коэффициентов парной корреляции , где у – результирующий признак, а х₁, х₂ … х_m – объясняющие факторы.

Однако, следует помнить, что прежде, чем применять формальные, математические методы отбора и выявления существенных факторов, следует провести тщательный содержательный анализ изучаемого объекта или процесса.

Рассмотренная выше задача нахождения точечного и интервального прогноза объема потребления дизельного топлива в 2005 г. носит скорее иллюстративный характер, т.е. предназначена для приобретения навыков нахождения точечных и интервальных прогнозов результирующего признака. Найденный интервальный прогноз [ŷ_Н, ŷ_В]=[2.764; 3.402] на 2005 г. показывает, что при выполнении сделанных предположений относительно объемов валового выпуска продукции сельского хозяйства и капитальных вложений в 2005 г. соответственно в размерах  руб. и   руб. следует с 90%-й уверенностью ожидать, что объем потребления дизельного топлива ŷ^np будет удовлетворять неравенству: 2.764≤ŷ^np≤3.402 (в млн. тонн).

Используемое в задачах 1, 2 понятие доверительной вероятности характеризует степень уверенности в справедливости получаемого результата. Чем ближе к единице значение доверительной вероятности (1-α), тем с большей уверенностью можно утверждать, что прогнозируемое значение результирующего признака будет находиться в найденном доверительном интервале. Следует иметь в виду, что ширина доверительного интервала существенно зависит от значения (1-α): чем ближе к единице величина (1-α), тем шире доверительный интервал и, следовательно, хуже качество прогноза.

Очевидно, что достаточной широкий доверительный интервал прогноза не имеет никакого практического значения. Действительно, если мы получим результат типа: «с вероятностью 0.999 среднее значение объема потребления дизельного топлива в 2005 г. будет находиться в пределах от 0 до 10 тонн», то от такого результата нет никакой практической пользы, несмотря на то, что степень его достоверности оценивается в 99.9%. поэтому при определении интервального прогноза приходится искать разумный компромисс между качеством прогноза, т.е. шириной доверительного интервала, и его достоверностью, т.е. значением доверительной вероятности.

В рамках задачи 2 можно рассмотреть задачу получения более точного и достоверного прогноза. Для этого следует сначала на основе трендовых моделей, рассмотренных ниже в задаче 3, найти точечные прогнозы на 2005 г. объемов валового выпуска продукции сельского хозяйства (х₁^np) и капитальных вложений (х₂^np). Затем, используя эти значения, найти точечный прогноз ŷ^np=α₀+α₁x₁^np+α₂x₂^np и интервальный прогноз по формуле ŷ_В,Н=ŷ(x^p)±.       

Задача 3.

3.1. Построить ломаную кривую изменения потребления дизельного топлива во времени. Выдвинуть гипотезу о виде зависимости объема потребления дизельного топлива от времени. Оценить неизвестные параметры модели методом наименьших квадратов.

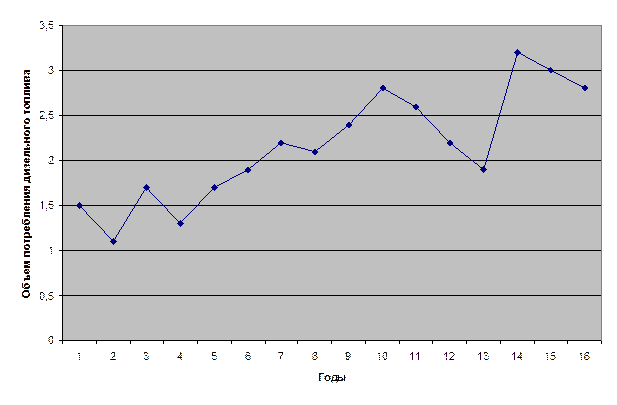
На основании визуального наблюдения ломаной кривой, отражающей характер изменения по годам объема потребления дизельного топлива, выдвигаем гипотезу о линейном тренде. Следовательно, трендовая модель, отображающая изменение потребления дизельного топлива, запишется в виде y=a₀+a₁t+u, где a₀, a₁ – неизвестные параметры, u – случайное отклонение.

Коэффициенты регрессионного уравнения тренда ŷ=a₀+a₁t находятся по методу наименьших квадратов из системы нормальных уравнений

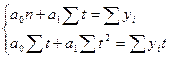
Следовательно,

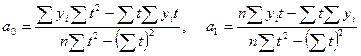
Подставив значения переменных, получим

a₀=1.21; a₁=0.11;

Следовательно, уравнение регрессии будет иметь вид:

y=1.21+0.11·t

3.2. Для найденного уравнения регрессии построить доверительную полосу при уровне доверия 0.9. Нарисовать ее на графике вместе с линией регрессии.

Решение.

Доверительный интервал для линейного тренда ŷ=a₀+a₁t находится по формуле:

 где y_в, y_н – соответственно верхняя и нижняя границы доверительного интервала; t_k – значение независимой переменной, для которой определяется доверительный интервал.

 – квантиль распределения Стьюдента (1–α) – доверительная вероятность, (n–2) – число степеней свободы.

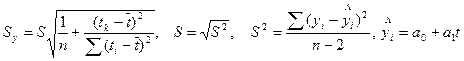
t_k – Номер года, для которого определяется доверительный интервал

 – выборочное среднее.

1–α/2=0.95; t_0.95,14 = 1.761

S²=0.1116

S=0.334

 = a₀+a₁·1=1.32

 = 0.16

 = 1.32+1.761·0.16 = 1.32+0.28 = 1.6

 = 1.32–1.761·0.16 = 1.32–0.28 = 1.04

Аналогично найдем доверительные интервалы для 1992 и 2000 годов.

Внесем вычисленные данные в таблицу.

Год	t
1985	1	1.32	0.16	1.6	1.04
1992	8	2.09	0.0211	2.053	2.127
2000	16	2.97	0.16	2.69	3.25

3.3. По линейному уравнению тренда найти точечный и интервальный прогноз среднего потребления дизельного топлива в 2005 г. и в 2007 г. (доверительную вероятность принять равной 0.9). Изобразить на графике точечный и интервальный прогноз.

Решение.

Точечный прогноз по линейному тренду на 2005 год находится  из уравнения регрессии. При этом t=21.

ŷ(21)=1.21+0.11·21=1.21+2.31=3.52

Аналогично находится точечный прогноз на 2007 год. При этом t=23.

ŷ(23)=1.21+0.11·23=1.21+2.53=3.74

Аналогично предыдущему пункту найдем.

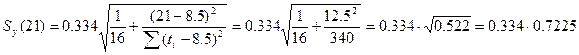 = 0.241

 = 3.52+1.761·0.241 = 3.52+0.42 = 3.92

 = 3.52–1.761·0.241 = 3.52–0.42 = 3.1

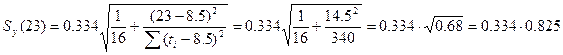 = 0.275

 = 3.74+1.761·0.275 = 3.74+0.48 = 4.22

 = 3.74–1.761·0.275 = 3.74–0.48 = 3.26

Задача 4.

4.1. Для уравнений регрессии  проверить наличие или отсутствие автокорреляции, используя критерий Дарбина-Уотсона при уровне значимости α=0.05.

Решение.

Проверка наличия или отсутствия автокорреляции ошибок регрессионного уравнения производится с помощью критерия Дарбина-Уотсона, который имеет вид: 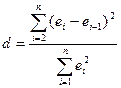, где e_i=ŷ_i–y_i – отклонения от линии регрессии.

Рассмотрим регрессионную модель , отражающую зависимость потребления дизельного топлива от объема валовой продукции сельского хозяйства и объема капитальных вложений. Уравнение регрессии найдено ранее: y=–0.626+0.26x₁+0.215x₂.

Значение знаменателя вычислено в п. 2.3. и равно 1.5462.

Значение числителя равно 0.5612

Т.к. d<d_e, то имеется положительная автокорреляция.

Аналогично рассчитываем параметры для остальных уравнений регрессии.

Регрессионная модель x₁=a₀+a₁·t

Коэффициенты регрессионного уравнения тренда x₁=a₀+a₁t находятся по методу наименьших квадратов из системы нормальных уравнений

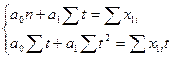
Следовательно,

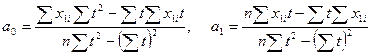
Подставив значения переменных, получим

a₀=5.1825; a₁=0.2653;

Следовательно, уравнение регрессии будет иметь вид:

x₁=5.1825+0.2653·t

Т.к. d<d_e, то имеется положительная автокорреляция.

Регрессионная модель x₂=b₀+b₁·t

Коэффициенты регрессионного уравнения тренда x₂=b₀+b₁t находятся по методу наименьших квадратов из системы нормальных уравнений

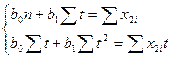
Следовательно,

Подставив значения переменных, получим

a₀=2.485; a₁=0.17;

Следовательно, уравнение регрессии будет иметь вид:

x₂=2.485+0.17·t

Т.к. d<d_e, то имеется положительная автокорреляция.

4.2. Для уравнения регрессии  проверить наличие или отсутствие мультиколлинеарности.

Решение.

Значение  найдено в пункте 2.1. и равно 0.925. Т.к. Это число близко к единице, то можно сделать вывод о том, что переменные x₁ и x₂ коррелируют между собой, т.е. между ними имеется нестрогая линейная зависимость и, следовательно, имеет место мультиколлинеарность.