Вариант 2.
Задача 1.
В 3 из 15 составленных кассиром счетов имеются ошибки.
Ревизор для проверки наугад выбирает 7 счетов из 15. Определить вероятность
того, что среди проверенных счетов: а) ни в одном счете не окажется ошибки; б)
в одном окажутся ошибки; в) хотя бы в одном окажутся ошибки.
Решение.
a) Перед
проверкой первого счета всего счетов 15, ошибочных – 3. Вероятность того, что
в первом счете нет ошибки – 12/15. Аналогично для второго счета эта вероятность
составит 11/14, для третьего – 10/13, для четвертого 9/12, для пятого – 8/11,
для шестого – 7/10, для седьмого – 6/9. В итоге получаем, что искомая
вероятность равна:
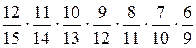 =
= 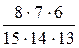 =
= 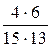 =
= 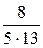 =
= 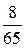
б) Вероятность того, что один (конкретный) счет из
проверенных окажется ошибочным равна 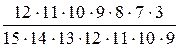 .
.
Следовательно, искомая вероятность получается
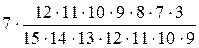 =
= 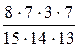 =
= 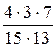 =
= 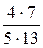 =
= 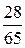
в) данное событие является дополнительным к первому событию,
следовательно его вероятность равна
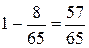 .
.
Задача 2.
При выпуске продукции в среднем 15% продукции является
браком. Найти вероятность того, что среди 400 изготовленных изделий доля годных
изделий будет не менее 80%, но не более 90%. Сколько нужно взять изделий, чтобы
указанная вероятность была бы равна 0.99?
Решение.
a) Доля
годных изделий в среднем – 1–0.15=0.85 найдем вероятность выполнения условий
для 400 деталей
P = 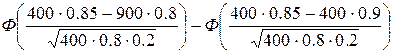 =
= 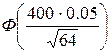 –
– 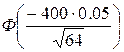 =
= 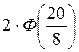 = 2∙Ф(2.5)
= 2∙0.4938 = 0.9876
= 98.76%
= 2∙Ф(2.5)
= 2∙0.4938 = 0.9876
= 98.76%
б) найдем количество деталей, для которого указанная
вероятность равна 0.99. Обозначим искомое число деталей N. Получим следующее условие
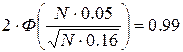
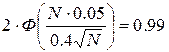
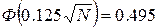
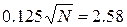
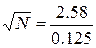
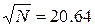
N=426.0096
Округлив до ближайшего целого получим искомое число деталей,
равное 426.
Задача 3.
Имеется 7 ключей, из которых только один подходит к замку.
Некто в темноте открывает замок, наугад пробуя ключи. Составить закон
распределения числа попыток при открывании замка, если испробованный ключ в
последующих опробованиях не участвует. Вычислить математическое ожидание и
дисперсию числа попыток; определить вероятность того, что будет произведено не
более трех попыток.
Решение.
Найдем закон распределения. Возможные значения искомой
случайной величины: 1, 2, 3, 4, 5, 6, 7.
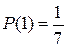
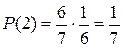
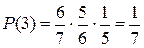
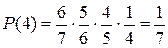
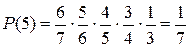
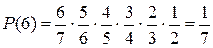
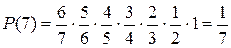
Сумма вероятностей всех исходов равна 1.
Математическое ожидание
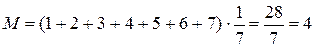
Дисперсия.
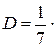 ((1–4)2+(2–4)2+(3–4)2+(4–4)2+(5–4)2+(6–4)2+(7–4)2)=
((1–4)2+(2–4)2+(3–4)2+(4–4)2+(5–4)2+(6–4)2+(7–4)2)=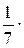 (32+22+12+ 12+22+32)=
(32+22+12+ 12+22+32)=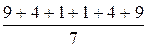 =
= 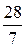 = 4
= 4
Вероятность того, что будет произведено не более 3 попыток =
P(1)+P(2)+P(3) = 1/7+1/7+1/7 = 3/7.
Задача 4.
Размер изделия определяется прибором, систематическая ошибка
которого равна нулю, а случайные ошибки нормально распределены со средним
квадратическим отклонением равным 0.5 мм. В качестве размера изделия берется
среднее выборочное значение ряда измерений. Сколько надо сделать измерений,
чтобы с надежностью 92% ошибка определения размера изделия не превышала 0.01
мм?
Решение.
Обозначим искомое количество измерений N. Необходимо найти такое N, при котором границы
доверительного интервала отстоят от выборочного среднего на расстояние 0.01 мм.
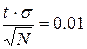 , где t удовлетворяет условию 2∙Ф(t)=0.92, а σ – среднеквадратическое
отклонение равное 0.5 мм. Найдем t.
, где t удовлетворяет условию 2∙Ф(t)=0.92, а σ – среднеквадратическое
отклонение равное 0.5 мм. Найдем t.
2∙Ф(t)=0.92
Ф(t)=0.46
t=1.75
Получаем уравнение для N.
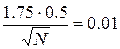
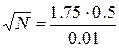
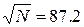
N=7656.25
Округлив до ближайшего целого, получим искомое число
измерений, равное 7657.
Задача 5.
Результаты роста X (см) и веса Y
(кг) 136 школьников приведены в следующей таблице:
|
Y
|
22.5–25.5
|
25.5–28.5
|
28.5–31.5
|
31.5–34.5
|
34.5–37.5
|
Всего
|
|
X
|
|
117.5–122.5
|
4
|
8
|
–
|
–
|
–
|
12
|
|
122.5–127.5
|
–
|
6
|
14
|
4
|
–
|
24
|
|
127.5–132.5
|
–
|
4
|
12
|
12
|
–
|
28
|
|
132.5–137.5
|
–
|
4
|
14
|
16
|
6
|
40
|
|
137.5–142.5
|
–
|
–
|
4
|
10
|
6
|
20
|
|
142.5–147.5
|
–
|
–
|
–
|
4
|
4
|
8
|
|
147.5–152.5
|
–
|
–
|
–
|
–
|
4
|
4
|
|
Всего
|
4
|
22
|
44
|
46
|
20
|
136
|
Предполагая, что между X и Y существует линейная корреляционная
зависимость, требуется: а) вычислить коэффициент корреляции и проанализировать
степень тесноты и направление связи; б) составить уравнения прямых регрессии и
построить их графики; в) используя соответствующее уравнение регрессии
определить рост школьника при весе в 45 кг.
Решение.
Так как значения переменных заданы промежутками, то для
вычисления статистических характеристик возьмем середины указанных отрезков.
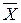 = (120∙12
+ 125∙24 + 130∙28 + 135∙40 + 140∙20 + 145∙8 + 150∙4)/136 = (1440 + 3000
+ 3640 + 5400 + 2800 + 1160 + 600)/136 = 18040/136=132.65
= (120∙12
+ 125∙24 + 130∙28 + 135∙40 + 140∙20 + 145∙8 + 150∙4)/136 = (1440 + 3000
+ 3640 + 5400 + 2800 + 1160 + 600)/136 = 18040/136=132.65
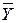 = (24∙4 + 27∙22
+ 30∙44 + 33∙46 + 36∙20)/136 = (96 + 594 + 1320 + 1518 + 720)/136 = 4248/136 = 31.24
= (24∙4 + 27∙22
+ 30∙44 + 33∙46 + 36∙20)/136 = (96 + 594 + 1320 + 1518 + 720)/136 = 4248/136 = 31.24
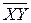 = (120∙24∙4
+ 120∙27∙8 + 125∙27∙6 + 125∙30∙14 + 125∙33∙4
+ 130∙27∙4 + 130∙30∙12 + 130∙33∙12 + 135∙27∙4
+ 135∙30∙14 + 135∙33∙16 + 135∙36∙6 + 140∙30∙4
+ 140∙33∙10 + 140∙36∙6 + 145∙33∙4 + 145∙36∙4
+ 150∙36∙4)/136 = (11520 + 25920 + 20250 + 52500 + 16500
+ 14040 + 46800 + 51480 + 14580 + 56700 + 71280 + 29160 + 16800 + 46200 + 30240
+ 19140 + 20880 + 21600)/136 = 565590/136 = 4158.75
= (120∙24∙4
+ 120∙27∙8 + 125∙27∙6 + 125∙30∙14 + 125∙33∙4
+ 130∙27∙4 + 130∙30∙12 + 130∙33∙12 + 135∙27∙4
+ 135∙30∙14 + 135∙33∙16 + 135∙36∙6 + 140∙30∙4
+ 140∙33∙10 + 140∙36∙6 + 145∙33∙4 + 145∙36∙4
+ 150∙36∙4)/136 = (11520 + 25920 + 20250 + 52500 + 16500
+ 14040 + 46800 + 51480 + 14580 + 56700 + 71280 + 29160 + 16800 + 46200 + 30240
+ 19140 + 20880 + 21600)/136 = 565590/136 = 4158.75
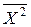 = (1202∙12
+ 1252∙24 + 1302∙28 + 1352∙40
+ 1402∙20 + 1452∙8 + 1502∙4)/136
= (172800 + 375000 + 473200 + 729000 + 392000 + 168200 + 90000)/136 = 2400200/136
= 17648,53
= (1202∙12
+ 1252∙24 + 1302∙28 + 1352∙40
+ 1402∙20 + 1452∙8 + 1502∙4)/136
= (172800 + 375000 + 473200 + 729000 + 392000 + 168200 + 90000)/136 = 2400200/136
= 17648,53
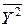 = (242∙4
+ 272∙22 + 302∙44 + 332∙46 +
362∙20)/136 = (2304 + 16038 + 39600 + 50094 + 25920)/136 = 133956/136
= 984,97
= (242∙4
+ 272∙22 + 302∙44 + 332∙46 +
362∙20)/136 = (2304 + 16038 + 39600 + 50094 + 25920)/136 = 133956/136
= 984,97
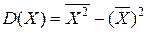 = 17648,53-132,652=17648,53-17596,0225=52,5075
= 17648,53-132,652=17648,53-17596,0225=52,5075
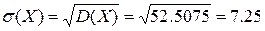
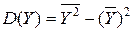 = 984,97-31,242=984,97-975,9376=9,0324
= 984,97-31,242=984,97-975,9376=9,0324
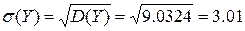
Коэффициент корреляции.
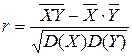 =
= 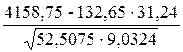 =
= 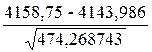 =
= 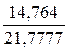 = 0.6779
= 0.6779
Т.к. r>0,
то связь прямая, т.е. с ростом одной переменной растет и другая, т.к. |r|=0.6779, то линейная связь
высокая.
Уравнение регрессии Y по X.
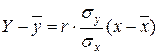
Y-31,24=0,6779∙(3,01/7,25)∙(x-132,65)
Y-31,24=0,28∙(x-132,65)
Y-31,24=0,28∙x-0,28∙132,65
Y-31,24=0,28∙x-37,142
Y=0,28∙x-5,902
Уравнение регрессии X по Y.
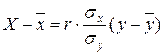
X-132,65=0,6779∙(7,25/3,01)∙(y-31,24)
X-132,65=1,63∙(y-31,24)
X-132,65=1,63∙y-1,63∙31,24
X-132,65=1,63∙y-50,9212
X=1,63∙y+81,7288
График.
При Y=45
по уравнению регрессии получим
X=1.63∙45+81.7288=155.0788