IV. Урок математики в начальной школе

Задание № 1

         При обучении математике возможно использовать разнообразные приемы формирования самостоятельной учебной деятельности, которые можно классифицировать следующим образом:

-сверка с образцом;

-повторное решение задачи;

-решение обратной задачи;

-проверка полученных результатов по условию задачи;

-решение задачи различными способами;

-моделирование;

-примерная оценка искомых результатов (прикидка);

-проверка на частном случае;

-испытание получаемых результатов по косвенным параметрам.

         Эта классификация приемов составлена С.Г. Манвеловым. Мы рассмотрим подробнее некоторые из них.

         Приучать учащихся к самопроверке следует уже на занятиях по арифметике, где это особенно просто, и продолжать в течение изучения всего курса математики. С первого класса необходимо нацеливать детей на то, что контролировать себя нужно сразу же, как только решили самостоятельно хотя бы один пример. Этим реализуется принцип немедленной проверки решения (решил пример - проверь себя; убедился, что твое решение верное - приступай к решению следующего примера). Такое положение в классе создается при определенных условиях. В качестве внешних условий вначале выступают материализованные индивидуальные средства обучения и использование их при самоконтроле на этапе объяснения и первичного закрепления нового учебного материала. Обучая элементам самоконтроля на этом этапе, главное выработать у детей потребность контролировать правильность полученных результатов. Этап самоконтроля с конкретными предметами должен перейти в этап самоконтроля заменителями предметов в виде рисунков, схем, чертежей и т.д. 

         Такой методический подход представляется весьма важным для того, чтобы приучить детей к самостоятельному составлению и решению обратных задач, что в последствии перейдет в потребность и необходимость контролировать решение прямой задачи при выполнении самостоятельных, домашних и контрольных работ. В подобных заданиях правильность решения прямой задачи проверяется решением обратной задачи, что позволяет быстрее обнаружить ошибки, выявить их причины, и на основе этого анализа внести соответствующие коррективы. Взаимообратные задачи (как и взаимообратные действия) обеспечивают взаимное подкрепление и постоянную обратную связь.

         Следующим приемом проверки решения текстовых задач является проверка по условию и смыслу задачи. “После решения задачи снова возвращаемся к ее условию. Прочитав сначала задачу полностью, разбиваем условие на отдельные смысловые части. В каждой части определяем, то ли число получается, если учесть найденный ответ”.

         Итак, одним из условий формирования навыка самоконтроля является умение детей проверять правильность решения текстовых задач. Проверка обычно осуществляется одним из следующих способов:

- проверка ответа по условию и смыслу задачи;

- составление и решение обратных задач;

- решение задач другими способами.

         В-третьих, для формирования навыка самоконтроля полезно приучить детей проверять справедливость выведенных формул на конкретных примерах.

         Следует заметить, что для формирования навыка самоконтроля не обязательно всегда проводить вычисления, иногда можно ограничиться составлением плана проверки, установлением последовательности действий. Проверку также можно проводить устно. Но это возможно только тогда, когда у учащихся уже выработался навык проведения контрольных действий над тем или видом математических упражнений.

         Фронтальные и взаимные проверки представляют собой промежуточное звено между контролем педагога и самоконтролем учащихся. Применение их имеет ряд преимуществ при обучении самоконтролю: положение контролеров обязывает учащихся лучше готовиться к занятиям, чтобы иметь возможность указать товарищу на допущенные им ошибки и установить их причины; коллективный анализ образца позволяет более полно выявить его сигнальные признаки и более углубленно их усвоить; разбирая разные способы сличения с образцом выполняемой работы, учащиеся отбирают те из них, которые наиболее целесообразны в данных условиях. Благодаря этому достигается большая точность сличения; коллективный анализ позволяет более полно выявить допущенные ошибки и установить их причины; в ходе коллективного поиска выявляются наиболее целесообразные способы исправления ошибок и внесения усовершенствований в выполняемую работу. Благодаря применению коллективных форм контроля учащиеся быстрее и лучше овладевают всеми звеньями индивидуального самоконтроля.

         Еще одним продуктивным приемом формирования самоконтроля являются математические диктанты, проводимые по определенной методике. В книге  “Самостоятельная работа учащихся в процессе обучения математике” описана методика проведения такого математического диктанта.

         При проведении такого математического диктанта возможно непосредственное обучение детей самоконтролю, связанное с целенаправленной организацией как взаимопроверки, так и самопроверки.   При проведении диктантов учитель должен четко представлять результативность некоторых видов работ:

проверка диктантов только учителем; взаимопроверка.

         Чтобы обеспечить высокое качество самоконтроля, необходимо организовать подготовку учащихся к его осуществлению. Эта подготовка включает в себя усвоение теоретического и практического материала, относящегося к предстоящей работе, анализ этой работы с целью выявления сенсорных признаков, служащих сигналами для самоконтроля; овладение приемами непосредственного и опосредованного самоконтроля и навыками работы с контрольно - измерительными инструментами и устройствами; овладение способами решения интеллектуальных задач; организацию упражнений с учащимися по овладению указанными признаками и приемами.

         Таким образом, наряду с использованием определенных приемов формирования самоконтроля, развитие этого навыка требует проведения специальных упражнений, структурно отличных от обычных распространенных упражнений. Это могут быть задания, рассчитанные на уяснение связей между прямыми и обратными теоремами, действиями и операциями. Специфика этих упражнений состоит в том, что учащимся приходится не просто выполнять задание, а так или иначе контролировать себя.

          В.И.Рыжик тоже рекомендует использовать некоторые упражнения для формирования навыка самоконтроля.

Учитель предлагает готовое решение какой-либо математической задачи, но оно является неправильным. Ошибки предлагается обнаружить ученикам.

Учитель приводит неполное решение задачи, а ученикам предлагает завершить его.

Для решения предлагается задача с неполными или избыточными данными, ученики должны обнаружить это.

Решение задачи, предлагаемое учителем, содержит принципиальные пробелы, которые предлагается найти ученикам.

         Мы считаем, что эти задания больше подходят для развития внимания детей, но их тоже необходимо использовать при формировании навыка самоконтроля, т.к. при отсутствии внимания не может быть речи ни о самоконтроле, ни о контроле вообще.

         Такие упражнения по формированию навыка самоконтроля усиливают ответственность у учащихся при выполнении заданий, приучают их работать без ошибок, а при выявлении - тут же их исправлять, и активизируют процесс обучения, пробуждают интерес к занятиям.

         Итак, формирование самоконтроля - процесс непрерывный. Он осуществляется под руководством учителя на всех стадиях процесса обучения (при изучении нового материала, при отработке навыков практической деятельности, при творческой самостоятельной работе учащихся и т.п.), начинается этот процесс еще в младших классах. Формируется навык самоконтроля посредством использования специальных приемов его формирования.

Задание № 2

Конспект урока на тему: «Порядок действий в выражениях без скобок».

Цели: закреплять умение решать уравнения, задачи на увеличение числа в несколько раз и уменьшение числа в несколько раз; отрабатывать навык сравнения выражений, нахождения значения выражения; научить детей определять порядок действий в выражениях без скобок; совершенствовать навык решения задач по действиям и выражением.

Оборудование: учебник по математике 2 класса А. Г. Петерсон; таблица с названием темы; таблица с примерами; карточки для индивидуальной работы.

Анализ: на данном уроке вводится правило порядка действий в выражениях без скобок. Фактически дети уже знакомы с этим правилом, но оно применялось лишь для выражений, содержащих 2 – 3 действия. А на данном уроке правило формулируется в общем виде и используется для решения примеров с более сложной структурой. Правило на уроке дети формулируют самостоятельно, что создает почву для мыслительной деятельности учащихся.

Для лучшего запоминания правила создается такой образ: знаки арифметических действий выстроились в очередь, первыми по порядку стоят знаки умножения и деления, а потом знаки сложения и вычитания. Этот момент носит элемент занимательности, что привлекает внимание учащихся.

Затем предлагаются  различные занимательные упражнения для закрепления данной темы.

Задание № 3

Задачи, показывающие не­которые доступные детям аспекты приме­нения комбинаторики в повседневной дея­тельности человека, например:

1. Малярам нужно покрасить б дачных домиков для малышей детского сада (кра­сят крышу, стены и дверь). У них есть синяя, голубая и белая краски. Могут ли маляры покрасить все дома по-разному, чтобы малыши по цвету узнавали свой дом?

Учащимся предлагается нарисовать 6 домиков, взять цветные карандаши и показать, как нужно выполнить работу малярам. Ответ изображен на рисунке 2.

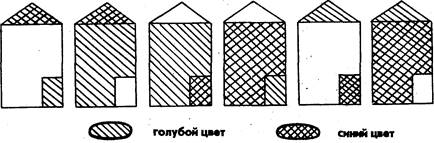 Рис. 2

2. В парке 4 пруда. Было решено за­сыпать песком дорожки между ними так, чтобы можно было пройти от одного пруда к другому кратчайшим путем, т.е. не нужно было идти в обход. Покажи, какие дорож­ки (рис. 3) будут сделаны.

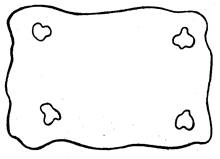Рис. 3     Рис. 4

                                                              Ответ изображен на рисунке 4.                                                                                                                                                                       

3. Художественный бланк телеграммы стоит 15 к., за доставку надо заплатить 25 к. Если телеграмма не срочная, то за каждое слово платят 6 к., если срочная, то за слово платят 25 к. Какую те­леграмму можно отправить, если есть 5 р. 30 к. и текст состоит из 20 слов? А если есть только 1 р. 50 к.?

Для решения данной задачи необходи­мо иметь и комбинаторные, и вычисли­тельные умения. Сначала определяют, ка­кие виды телеграмм возможны: срочная на художественном бланке, срочная на обыкновенном бланке, не срочная на худо­жественном бланке, не срочная на обыкно­венном бланке. Затем подсчитывают стои­мость телеграммы в каждом случае и срав­нивают с числом имеющихся денег.

4. У кассы кинотеатра стоят четверо ребят. У двух из них рубли, у других двух полтинники. (Учитель вызывает 4 учеников к доске и дает им модели монет.) Билет в кино стоит 50 к. В начале продажи касса пуста. (Учитель вызывает «кассира» и дает ему «билеты».) Затем формули­руется задача: «Как должны расположиться ребята, чтобы никому не пришлось ждать сдачи?»

Разыгрывая сценку, ученики находят два возможных варианта:

а) 50 к., 1 р., 50 к., 1 р.

б) 50 к., 50 к., 1 р., 1 р.

Затем предлагается решить: «Что произой­дет в том случае, когда у двоих полтин­ники, а у троих рубли?» (В этом случае одному человеку кассир не сможет дать сда­чи.)

V. Определение «математика»

Советские математики рассматривают ма­тематические понятия не как создание чистого разума, а как абстракции от реально существующих вещей, явлений, процессов или же абстракции от уже сложившихся абстракций (абстракции высших порядков). В «Диалек­тике природы» Ф. Энгельс писал, что «... вся так называемая чистая математика занимает­ся абстракциями,  все ее величины суть, стро­го говоря, воображаемые величины». Эти слова достаточно четко отражают мнение одного из основоположников марксистской философии о роли абстракций в математике. Нам только следует добавить, что все эти «воображаемые величины» берутся из реаль­ной действительности, а не конструируются произвольно, свободным полетом мысли. Именно так вошло во всеобщее употребле­ние понятие числа. При этом всегда следует помнить прекрасные слова Ф. Энгельса: «... чистая математика имеет значение, независимое от особого опы­та каждой отдельной личности... Но совершенно неверно, будто в чистой математике разум имеет дело только с продуктами соб­ственного творчества и воображения. Понятия числа и фигуры взяты не откуда-нибудь, а только из действительного мира. Десять пальцев, на которых люди научились считать, т.е. производить первую арифметическую операцию, представляют собой все, что угод­но, только не продукт свободного творчества

разума. Чтобы считать, надо иметь не только предметы, подлежащие счету, но обладать уже и способностью отвлекаться при рассмот­рении этих предметов от всех прочих свойств, кроме числа, а эта способность есть результат долгого исторического развития, опирающе­гося на опыт. Как понятие числа, так и поня­тие фигуры заимствовано исключительно из внешнего мира, а не возникло в голове из чистого мышления. Должны были существовать вещи, имеющие определенную форму, и эти формы должны были подвергаться сравне­нию, прежде чем можно было прийти к поня­тию фигуры».

Итак, мы рассказали, что же входит в поня­тие «математика». Но существует еще и такое понятие, как прикладная математика. Под ним понимают совокупность всех математи­ческих методов и дисциплин, находящих при­менения за пределами математики. Прикладная математика пополнилась новым очень мощным методом исследования - математическим    анализом. Математика, прежде чем изучать своими методами какое-нибудь явление, создает его математическую модель, т.е. перечисляет все те особенности явления, которые будут приниматься во внимание. Модель при­нуждает исследователя выбирать те матема­тические средства, которые позволят вполне адекватно передать особенности изучаемого явления и его эволюции.

VII. Написать сообщение

 В своей практике естествоиспытателю приходится обрабатывать большие массивы данных, полученных в результате эксперимента путем измерений, наблюдений, анализа проб и т.п. Часто этим данным присуща изменчивость, вызванная случайными ошибками. Природа этих ошибок может быть различной: погрешность измерительных приборов, неоднородность образцов проб и др. Как правило, экспериментатор имеет возможность многократно повторить свой опыт и получить большое количество однородных данных. Затем перед исследователем встает задача обработки этих данных, чтобы извлечь как можно более точную информацию об измеряемой величине. Мы приступаем к изложению базовых принципов и методов статистической обработки данных.

Задачи, решаемые математической статистикой, являются, в некотором смысле, обратными задачам теории вероятностей. Вероятностные задачи, как правило, устроены следующим образом: распределения случайных величин считаются изначально известными, основываясь на знании этих распределений требуется найти вероятности различных событий, математические ожидания, дисперсии, моменты распределений и т.п. В статистических задачах само распределение считается неизвестным, и целью исследования является получение более или менее достоверной информации об этом распределении на основе данных, собранных в результате наблюдений (экспериментов).

Литература

1.     Начальная школа.- 1992.- № 1.- С. 20-22

2.     Сборник "Программы общеобразовательных учреждений. Начальные классы.Часть 1 (1-4 классы)", 2000, Просвещение Перечень-каталог учебно-методических изданий для общеобразовательных учреждений на 2002/2003 учебный год. Раздел I.